分治

第七章 分治

    所谓分治就是指的分而治之，即将较大规模的问题分解成几个较小规模的问题，通过对较小规模问题的求解达到对整个问题的求解。当我们将问题分解成两个较小问题求解时的分治方法称之为二分法。

    你们玩过猜数字的游戏吗？你的朋友心里想一个1000以内的正整数，你可以给出一个数字x，你朋友只要回答“比x大”或者“比x小”或者“猜中”，你能保证在10次以内猜中吗？运气好只要一次就猜中。

   开始猜测是1到1000之间，你可以先猜500，运气好可以一次猜中，如果答案比500大，显然答案不可能在1到500之间，下一次猜测的区间变为501到1000，如果答案比500小，那答案不可能在500到1000之间，下一次猜测的区间变为1到499。只要每次都猜测区间的中间点，这样就可以把猜测区间缩小一半。由于    ，因此不超过10次询问区间就可以缩小为1，答案就会猜中了，这就是二分的基本思想。

    每一次使得可选的范围缩小一半，最终使得范围缩小为一个数，从而得出答案。假设问的范围是1到n，根据,所以我们只需要问O(logn)次就能知道答案了。

需要注意的是使用二分法有一个重要的前提，就是有序性，下面通过几个例子来体会二分法的应用。

找数这个简单吧，二分来一波

 

找数问题

【题目描述】：

给一个长度为n的单调递增的正整数序列，即序列中每一个数都比前一个数大。有m个询问，每次询问一个x，问序列中最后一个小于等于x的数是什么？

输入：

第一行两个整数n,m。

接下来一行n个数，表示这个序列。

接下来m行每行一个数，表示一个询问。

输出：

输出共m行，表示序列中最后一个小于等于x的数是什么。假如没有输

【算法分析】：
我们用Left表示询问区间的左边界，用Right表示询问区间的右边界，[Left,Right]组成询问区间。一开始Left=1，Right=n，我们可以把原始序列的左边想象成若干个无穷小的数，把序列的右边想象成无穷大的数，这样比较好理解。序列已经按照升序排好，保证了二分的有序性。
每一次二分，我们这样来做：
    ①取区间中间值Mid=(Left+Right)/2；
    ②判断Mid与x的关系，如果a[Mid]>x，由于序列是升序排列，所以区间[Mid,Right]都可以被排除，修改右边界Right=Mid-1；
    ③如果a[Mid]<=x，修改左边界Left=Mid+1；
重复执行二分操作直到Left>Right。
    下面我们来分析答案的情况。循环结束示意图如下：LeftRight大于x小于等于x

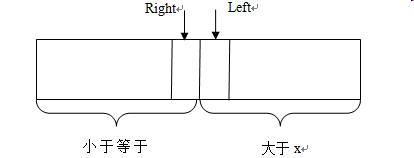
 最终循环结束时一定是Left=Right+1，根据二分第②步的做法我们知道Right的右边一定都是大于x的，而根据第③步我们可以知道Left左边一定是小于等于x的。
    所以，一目了然，最终答案是Right指向的数。Right=0就是题目中输出-1的情况。

突然好想你，最长不下降子序列Nlogn

【分析】：

定义：a[1..n]为原始序列，d[k]表示长度为k的不下降子序列末尾元素的最小值，len表示当前已知的最长子序列的长度。

初始化：d[1]=a[1]; len=1; （0个元素的时候特判一下）

现在我们已知最长的不下降子序列长度为1，末尾元素的最小值为a[1]，那么我们让i从2到n循环，依次求出前i个元素的最长不下降子序列的长度，循环的时候我们只需要维护好d这个数组还有len就可以了。

关键问题就是怎么维护？

可以看出我们是要用logn的复杂度维护的。实际上利用了d数组的一个性质：单调性。（长度更长了，d[k]的值是不会减小的）

考虑新进来一个元素a[i]：

如果这个元素大于等于d[len]，直接让d[len+1]=a[i]，然后len++。这个很好理解，当前最长的长度变成了len+1，而且d数组也添加了一个元素。

如果这个元素小于d[len]呢？说明它不能接在最后一个后面了。那我们就看一下它该接在谁后面。

准确的说，并不是接在谁后面。而是替换掉谁。因为它接在前面的谁后面都是没有意义的，再接也超不过最长的len，所以是替换掉别人。那么替换掉谁呢？就是替换掉那个最该被它替换的那个。也就是在d数组中第一个大于它的。第一个意味着前面的都小于等于它。假设第一个大于它的是d[j]，说明d[1..j-1]都小于等于它，那么它完全可以接上d[j-1]然后生成一个长度为j的不下降子序列，而且这个子序列比当前的d[j]这个子序列更有潜力（因为这个数比d[j]小）。所以就替换掉它就行了，也就是d[j]=a[i]。其实这个位置也是它唯一能够替换的位置（前面的替了不满足d[k]最小值的定义，后面替换了不满足不下降序列）

至于第一个大于它的怎么找……STL upper_bound。每次复杂度logn。

【代码实现】：

//最长不下降子序列nlogn  Song

    d[1]=a[1];  //初始化

    int len=1;

    for (int i=2;i<=n;i++)

    {

        if (a[i]>=d[len]) d[++len]=a[i];  

//如果可以接在len后面就接上，如果是最长上升子序列，这里变成>

        else  //否则就找一个最该替换的替换掉

        {

            int j=upper_bound(d+1,d+len+1,a[i])-d;  

//找到第一个大于它的d的下标，如果是最长上升子序列，这里变成lower_bound

            d[j]=a[i];

        }

}

【总结】：

1. 个人感觉是递归的升级版，只不过是侵略性地排除答案，再一层一层地排查，速度很快
2. 听说有优先队列这个东西了解一下，优先队列是什么，就是个堆，一个有顺序的数组

感谢各位与信奥一本通的鼎力相助！