题目


测试得分: 100
主要算法 : DP(零一背包,完全背包)
题干:
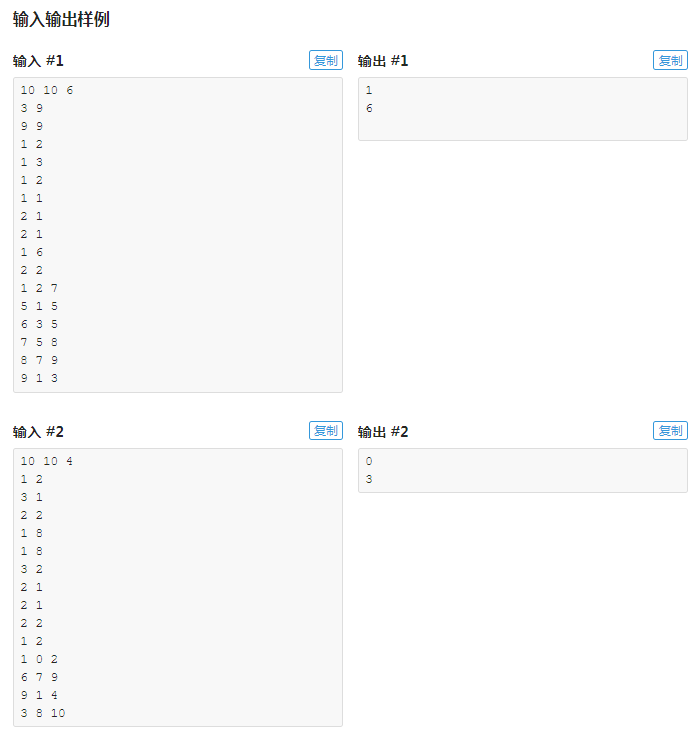
背包组合问题
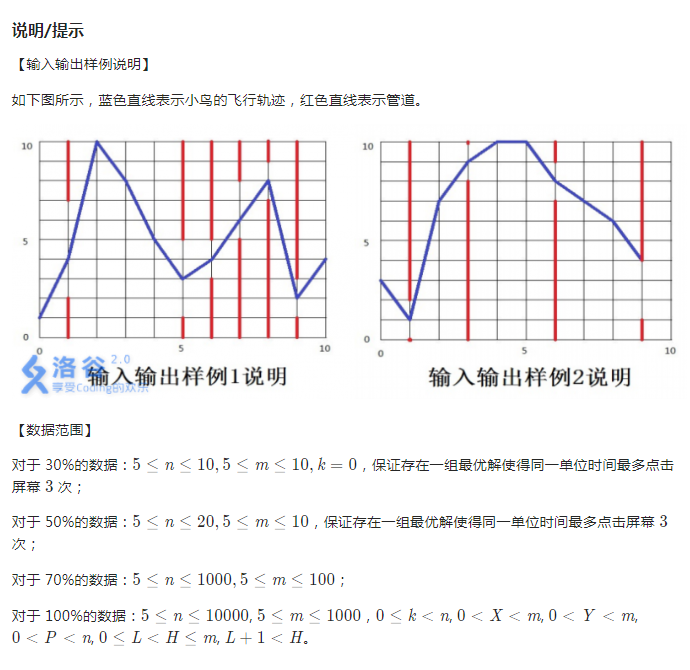
应试策略:
-
每一个点都是由前面的状态转移的,并且对后面的状态没有影响,满足最优化原理与无后效性原则,选择算法DP
- 对于图上的每一个点都是由前一列降下来或者是前面升上来的,对于降下来的情况是零一背包,上升的情况是完全背包,但是考场的时候,上升的情况是一一枚举可以跳几步,并且是由前一列转移过来的,所以其实复杂度是不对的,其次对转移的时候每一次都在判断是不是柱子或者这个点转移不过来,简单的说就是此前这个点没有更新,则这个点是荒废的,又增加了时间的累赘
- 没有判断每一个点升高与降低的特殊情况,每一次转移的时候,会产生遗漏计算的点
代码
#include<stdio.h> #include<stdlib.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) #define gc pa==pb&&(pb=(pa=buf)+fread(buf,1,100000,stdin),stdin)?EOF:*pa++ #define File(name) freopen(name".in","r",stdin);freopen(name".out","w",stdout); using namespace std; char buf[100000],*pa,*pb; inline int read(); const int N=10000,M=1000,INF=214748364; int n,m,k,ans=INF; int f[N+2][M+2]; struct Sp{ int x,y; }sp[N+1]; struct Tube{ int x,l,h; }tube[N+1]; int sum[N+1]; inline int min(int fa,int fb){return fa<fb?fa:fb;} void Init() { n=read(),m=read(),k=read(); FORa(j,0,m) f[0][j]=0; FORa(i,1,n) FORa(j,0,m) f[i][j]=INF; FORa(i,1,n) sp[i].x=read(),sp[i].y=read(); FORa(i,1,k) { tube[i].x=read(),tube[i].l=read(),tube[i].h=read(); sum[tube[i].x]=1; FORa(j,0,tube[i].l) f[tube[i].x][j]=-1; FORa(j,tube[i].h,m) f[tube[i].x][j]=-1; } FORa(i,1,n) sum[i]+=sum[i-1]; } void Solve() { int p,s; FORa(i,1,n) { bool flag=1; FORa(j,1,m) { if(f[i][j]==-1) continue; if(j==m)//特判 { p=f[i][j]; for(int l=1;l<=m;l++) { if(f[i-1][l]!=-1&&f[i-1][l]!=INF) if(l!=m) p=min(f[i-1][l]+(m-l)/sp[i].x+bool((m-l)%sp[i].x),p);//防止l==m的时候bool((m-l)%sp[i].x)=0的错误时事件 else p=min(f[i-1][l]+1,p); } f[i][j]=p; if(p!=-1&&p!=INF) flag=0; continue; } p=f[i][j],s=1; if(j+sp[i].y<=m&&f[i-1][j+sp[i].y]!=-1&&f[i-1][j+sp[i].y]!=INF) p=min(f[i-1][j+sp[i].y],p);//零一背包 while(j>s*sp[i].x&&sp[i].x&&f[i-1][j-s*sp[i].x]!=-1&&f[i-1][j-s*sp[i].x]!=INF) p=min(f[i-1][j-s*sp[i].x]+s,p),s++;//完全背包 f[i][j]=p; if(p!=-1&&p!=INF) flag=0; } if(flag) { printf("0 %d",sum[i-1]); return; } } FORa(i,1,m) if(f[n][i]!=-1&&f[n][i]!=INF) ans=min(ans,f[n][i]); printf("1 %d",ans); } int main() { //File("bird"); Init(),Solve(); return 0; } inline int read() { register char c(gc);register int x(0),f(1); while(c<'0'||c>'9') f=c=='-'?-1:1,c=gc; while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=gc; return x*f; }
分析:
-
对于完全背包的处理:对于当h>m的时候,因为题目的限制,h=m,但是对于h<=m+sp[i].x需要进入f[i][m]的状态转移中,这里就向一些dalao学习了一种巧妙的解决方法,直接将f[i][j]的第二下标的上限转换为m+sp[i].x,随后将这些“越界”的状态转移到f[i][m]
FORa(j,sp[i].x+1,sp[i].x+m) f[i][j]=min(f[i][j-sp[i].x],f[i-1][j-sp[i].x])+1; FORa(j,m+1,m+sp[i].x) f[i][m]=min(f[i][m],f[i][j]);
2. 对于零一背包直接转移
FORa(j,1,m-sp[i].y) f[i][j]=min(f[i][j],f[i-1][j+sp[i].y]);
3. 如果有柱子怎么办,我可能还是处理了,对了,有人会问为什么不要判断是不是柱子或者这个点转移不过来,这是因为我们求的是min,所以非答案的“答案值”会自动过滤掉,这也是为什么我们要每一次将柱子重新设置一个极大的值的原因
代码
#include<stdio.h> #include<stdlib.h> #include<string.h> #define FORa(i,s,e) for(int i=s;i<=e;i++) #define FORs(i,s,e) for(int i=s;i>=e;i--) #define gc pa==pb&&(pb=(pa=buf)+fread(buf,1,100000,stdin),stdin)?EOF:*pa++ #define File(name) freopen(name".in","r",stdin);freopen(name".out","w",stdout); using namespace std; char buf[100000],*pa,*pb; inline int read(); const int N=10000,M=1000; int n,m,k,ans; int f[N+1][3*M+2]; struct Sp{ int x,y,vis,s,e; }sp[N+1]; inline int min(int fa,int fb){return fa<fb?fa:fb;} void Init() { n=read(),m=read(),k=read(); memset(f,63,sizeof(f)); FORa(j,1,m) f[0][j]=0; FORa(i,1,n) sp[i].x=read(),sp[i].y=read(),sp[i].s=1,sp[i].e=m; int id; FORa(i,1,k) id=read(),sp[id].vis=1,sp[id].s=read()+1,sp[id].e=read()-1; } void Solve() { FORa(i,1,n) { FORa(j,sp[i].x+1,sp[i].x+m) f[i][j]=min(f[i][j-sp[i].x],f[i-1][j-sp[i].x])+1; FORa(j,m+1,m+sp[i].x) f[i][m]=min(f[i][m],f[i][j]); FORa(j,1,m-sp[i].y) f[i][j]=min(f[i][j],f[i-1][j+sp[i].y]); FORa(j,0,sp[i].s-1) f[i][j]=f[0][0]; FORa(j,sp[i].e+1,m) f[i][j]=f[0][0]; } ans=f[0][0]; FORa(j,1,m) ans=min(ans,f[n][j]); if(ans!=f[0][0]) printf("1 %d",ans); else { int i,j; ans=0; for(i=n;i>=1;i--) { for(j=1;j<=m;j++) if(f[i][j]<f[0][0]) break; if(j<=m) break; } FORa(l,1,i) if(sp[l].vis) ans++; printf("0 %d",ans); } } int main() { File("bird"); Init(),Solve(); return 0; } inline int read() { register char c(gc);register int x(0),f(1); while(c<'0'||c>'9') f=c=='-'?-1:1,c=gc; while(c>='0'&&c<='9') x=(x<<1)+(x<<3)+c^48,c=gc; return x*f; }
总结:
1.确定DP类型与状态转移的健全性
2.避免做无意义的事情
