学习
数据挖掘的流程
数据预处理->数据探索->模型训练->模型选择->模型评估
模型选择
模型选择是对超参数的选择,通过校验集,来看看模型那一组超参数有更好的效果
模型评估
分类
分类问题的常用评估指标有准确率(accuracy)、精确率(precision)、召回率(recall)、F1_score、ROC曲线()等等,它们都可以基于混淆矩阵(confusion matrix)来进行计算
(1)混淆矩阵:二分类问题混淆矩阵如图所示:
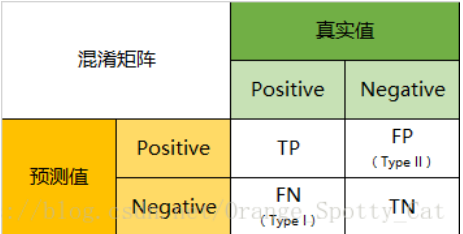
P为Positive正类的意思,N为Negative负类的意思,T为True真的意思、F为False假的意思,举个例子,TP就是预测结果为Positive,同时预测结果为真(真实结果也为positive)。下面为混淆矩阵的代码实现:
#二分类问题
from sklearn.metrics import confusion_matrix
y_pre = np.array([0, 1, 1, 1, 0])
y_tru = np.array([1, 1, 0, 0, 0])
confusion_mat = confusion_matrix(y_pre, y_tru) # predict_value为行,true_value为列
print(confusion_mat)
[[1 1]
[2 1]]
| 实际类别0 | 实际类别1 | |
|---|---|---|
| 预测类别0 | 1 | 1 |
| 预测类别1 | 2 | 1 |
#多分类问题
y_pre = np.array([1, 1, 0, 2, 1, 0, 1, 3, 3])
y_tru = np.array([1, 0, 0, 2, 1, 0, 3, 3, 3])
confusion_mat = confusion_matrix(y_pre, y_tru)
print(confusion_mat)
[[2 0 0 0]
[1 2 0 1]
[0 0 1 0]
[0 0 0 2]]
| 实际类别0 | 实际类别1 | 实际类别2 | 实际类别3 | |
|---|---|---|---|---|
| 预测类别0 | 2 | 0 | 0 | 0 |
| 预测类别1 | 1 | 2 | 0 | 1 |
| 预测类别2 | 0 | 0 | 1 | 0 |
| 预测类别3 | 0 | 0 | 0 | 2 |
(2)准确率、精确率、召回率:有了混淆矩阵后,就可以计算一些指标了。准确率公式为(Accuracy = frac{TP+TN}{TP+TN+FP+FN}); 精确率公式为(Precision = frac{TP}{TP+FN}); 召回率的公式为(Recall = frac{TP}{TP+FN})。下面为具体的代码实现:
#准确率、精确率、召回率
y_pre = [0, 1, 1, 0, 1]
y_tru = [0, 0, 0, 0, 1]
confusion_mat = confusion_matrix(y_pre, y_tru)
accuracy = sum([confusion_mat[i, i] for i in range(len(confusion_mat))]) / np.sum(confusion_mat)
precision = confusion_mat[1, 1] / np.sum(confusion_mat[1]) #对于类别而言
recall = confusion_mat[1,1] / np.sum(confusion_mat[: 1])
print('准确率Accuracy={}'.format(accuracy))
print('精确率Precision={}'.format(precision))
print('召回率Recall={}'.format(recall))
准确率Accuracy=0.6
精确率Precision=0.3333333333333333
召回率Recall=0.5
(3)F1_score:往往精确率和召回率是不可兼得的事情,所以我们需要一个综合两者的指标F1_score,为什么选择F1_score,而不选择mean呢?原因。其公式为(F1_score = frac{2cdot pcdot r}{p + r})。下面为具体的代码实现:
#F1_score
f1_score = 2 * precision * recall / (precision + recall)
print('F1_score={}'.format(f1_score))
F1_score=0.4
其实上面的指标都可以用一个函数实现
from sklearn.metrics import classification_report
y_pre = [0, 1, 1, 0, 1]
y_tru = [0, 0, 0, 0, 1]
print(classification_report(y_tru, y_pre))
precision recall f1-score support
0 1.00 0.50 0.67 4
1 0.33 1.00 0.50 1
accuracy 0.60 5
macro avg 0.67 0.75 0.58 5
weighted avg 0.87 0.60 0.63 5
(4)ROC(Receiver Operating Characteristic Curve)曲线和AUC(Area under roc Curve):上面的的评价指标适合与输出为具体分类标签的分类问题(或者已经给定概率阀值),可是有些分类问题输出的是每种分类的结果的概率,所以我们需要引入ROC曲线和AUC值。
首先我们先规定分类中的正类,其余为负类,然后我们定义真阳性率(TPR = frac{TP}{P}),假阳性率(FPR = frac{FP}{N})。下面举个例子来理解真阳性率和假阳性率:一个人被给予若干张动物然后进行分类,我们先规定猫为正类,那么真阳性率在这里就指的是在所有的猫图片中被分类为猫的概率,假阳性率中所有不是猫的图片被分类为猫的概率,简单的来说就是正确判断率和误判率。理解了真阳性率和加阳性率后,下面就可以构建ROC曲线。假设通过分类模型,我们得到了测试集中正类的概率序列([0.1, 0.2, 0.5, 0.8]),那么取不同的概率阀值,就会对应不同的预测值,比如当阀值=0.5时,大于等于阀值的会被预测为正类,小于阀值则预测为负类,预测序列为[非正,非正,正,正], 那么根据真实结果序列就可以计算出对应的(FPR, TPR)。我们让阀值去遍不同的值,就会得到一系列的(FPR, TPR)点,在坐标轴上绘制就得到了ROC曲线。
那么如何利用ROC曲线进行模型评估呢?那么则需要AUC,即ROC曲线包围的面积值。显然,AUC值越高,所对应的模型越好。
下面为具体的代码实现:
from sklearn.metrics import roc_curve, auc
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = roc_curve(y_true, y_scores, pos_label=0)
print('roc曲线为')
print('fpr={}'.format(fpr))
print('tpr={}'.format(tpr))
print('thresholds={}'.format(thresholds))
auc_value = auc(fpr, tpr)
print('auc={}'.format(auc_value))
roc曲线为
fpr=[0. 0.5 0.5 1. 1. ]
tpr=[0. 0. 0.5 0.5 1. ]
thresholds=[1.8 0.8 0.4 0.35 0.1 ]
auc=0.25
回归
sklearn
sklearn是做数据挖掘经常使用的python库,在此记录一些用法。当然最好的参考资料永远是官方文档
转换器
为什么要转换器
sklearn中的转换器是什么的呢?假设目前这个场景,你想对测试集上输入部分做同训练集一样归一化的处理((x' = frac{x-min}{max-min})),那么一般会这样做。
import numpy as np
#自定义训练集和测试集
X_train = np.array([[1, 2], [3, 4]], dtype='float')
X_test = np.array([[2, 2], [3, 3]], dtype='float')
#训练集每列的最大最小值
min0, max0 = min(X_train[:, 0]), max(X_train[:, 0])
min1, max1 = min(X_train[:, 1]), max(X_train[:, 1])
print('训练集X_train=')
print(X_train)
print('训练集X_train的第0列的最大值为{}, 最小值为{}'.format(max0, min0))
print('训练集X_train的第1列的最大值为{}, 最小值为{}'.format(max1, min1))
#对训练集进行归一化处理
for i in range(X_train.shape[0]):
for j in range(X_train.shape[1]):
if j == 0:
X_train[i][j] = (X_train[i][j] - min0) / (max0 - min0)
else:
X_train[i][j] = (X_train[i][j] - min1) / (max1 - min1)
print('归一化后的训练集为X_train=')
print(X_train)
训练集X_train=
[[1. 2.]
[3. 4.]]
训练集X_train的第0列的最大值为3.0, 最小值为1.0
训练集X_train的第1列的最大值为4.0, 最小值为2.0
归一化后的训练集为X_train=
[[0. 0.]
[1. 1.]]
#再对测试集做相同的处理
print('原测试集X_test=')
print(X_test)
for i in range(X_test.shape[0]):
for j in range(X_test.shape[1]):
if j == 0:
X_test[i][j] = (X_test[i][j] - min0) / (max0 - min0)
else:
print(X_test[i][j])
X_test[i][j] = (X_test[i][j] - min1) / (max1 - min1)
print('归一化后的测试集X_test=')
print(X_test)
原测试集X_test=
[[2. 2.]
[3. 3.]]
2.0
3.0
归一化后的测试集X_test=
[[0.5 0. ]
[1. 0.5]]
可以看到,上面对测试集归一化非常的麻烦,并且我们还需要记录下训练集的最大最小值,所以sklearn中使用了转换器来简略操作。
import numpy as np
from sklearn.preprocessing import MinMaxScaler
#自定义训练集和测试集
X_train = np.array([[1, 2], [3, 4]], dtype='float')
X_test = np.array([[2, 2], [3, 3]], dtype='float')
ms = MinMaxScaler()
ms.fit(X_train)
X_test = ms.transform(X_test)
print(X_test)
[[0.5 0. ]
[1. 0.5]]
在这里其中转换器的fit操作相当于记录训练集中每一列的极值并保存起来,transform函数就相当于用保存的极值对测试集进行归一化
一般来说,fit就是用来保存通过训练集得到的关键信息,transform就是用fit得到的关键信息来处理测试集,fit_transform则是合并2个函数
自定义转换器
虽然sklearn提供转换器可以满足大多数问题的需要,但是总会遇到已有转换器无法解决的问题,所以我们需要自定义转换器。
下面我们来制作和MinMaxScaler转换器一样功能的转换器
import numpy as np
import pandas as pd
#导入自定义转换器所需要的基类
from sklearn.base import BaseEstimator, TransformerMixin
#定义自定义转换器,重写fit和transform函数
class MyMinMaxScaler(BaseEstimator, TransformerMixin):
def fit(self, X, y=None):
self.min = np.min(X, axis=0)
self.max = np.max(X, axis=0)
return self
def transform(self, X, y=None):
X = X.copy()
return (X-self.min) / (self.max-self.min)
X_train = np.array([[1, 2], [3, 4]], dtype='float')
X_test = np.array([[2, 2], [3, 3]], dtype='float')
ms = MyMinMaxScaler()
ms.fit(X_train)
X_test = ms.transform(X_test)
print(X_test)
[[0.5 0. ]
[1. 0.5]]
估计器
估计器是sklearn提供的应一个强大的类,它封装了某个模型,比如决策树模型、贝叶斯模型,使用者可以创建估计器对象创建模型,调用fit方法训练模型,调用predict或者predict_proba来预测结果。例如:
import sklearn.tree as tree
#创建模型
clf = tree.DecisionTreeClassifier()
#训练模型
clf.fit(X_train)
#预测结果
clf.predict(X_test)
管道
连接n个转换器
注意:连接n个转换器后得到的管道视为一个转换器
举个例子:假设目前我们有两个转换器,我们会这样使用
import numpy as np
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import MinMaxScaler
from sklearn.pipeline import Pipeline
#自定义训练集、测试集
X_train = np.array([[1, np.nan, 3],[np.nan, 2, 3],[3, 5, np.nan]])
X_test = np.array([[2, np.nan, 3],[np.nan, 2, 3],[3, 4, np.nan]])
#定义转换器
imputer = SimpleImputer(strategy='most_frequent')
scaler = MinMaxScaler()
#通过训练集获取转换器关键参数
X_train_1 = imputer.fit_transform(X_train)
scaler.fit(X_train_1)
#对测试集做相同处理
X_test_1 = imputer.transform(X_test)
X_test_2 = scaler.transform(X_test_1)
print(X_test_2)
[[0.5 0. 0. ]
[0. 0. 0. ]
[1. 0.66666667 0. ]]
同样这里比较麻烦,可以用Pipeline对象将多个转换器连接起来,起到一个转换器的效果
# 自定义训练集、测试集
X_train = np.array([[1, np.nan, 3],[np.nan, 2, 3],[3, 5, np.nan]])
X_test = np.array([[2, np.nan, 3],[np.nan, 2, 3],[3, 4, np.nan]])
pipeline = Pipeline(steps=[
('imputer', SimpleImputer(strategy='most_frequent')),
('scaler', MinMaxScaler())
])
pipeline.fit(X_train)
X_test_ = pipeline.transform(X_test)
print(X_test_)
[[0.5 0. 0. ]
[0. 0. 0. ]
[1. 0.66666667 0. ]]
连接n个转换器和1个评估器
注意:连接n个转换器和1个评估器得到的管道视为一个评估器
调用fit函数会依次调用转换器的fit_transform函数,最后在调用估计器的fit函数进行训练
调用predict或者predict_proba函数则是会依次调用转换器的transform函数对测试集做和训练集相同的处理,最后在调用估计器的predict或predict_proba函数进行预测
numpy
pandas
concat函数
该函数用于DataFrame对象的链接,下面举具体的例子:
# axis=0 行合并
import pandas as pd
df1 = pd.DataFrame({'name': ['小明', '小红'], 'color': ['蓝', '红']})
df2 = pd.DataFrame({'name': ['小黑', '小白'], 'color': ['黑', '白']})
df_concat = pd.concat([df1, df2], axis=0)
print('df1=')
print(df2)
print()
print('df2=')
print(df2)
print()
print('行合并结果为')
print('df_concat=')
print(df_concat)
df1=
name color
0 小黑 黑
1 小白 白
df2=
name color
0 小黑 黑
1 小白 白
行合并结果为
df_concat=
name color
0 小明 蓝
1 小红 红
0 小黑 黑
1 小白 白
# axis=1 列合并
import pandas as pd
df1 = pd.DataFrame({'name': ['小黑', '小白'], 'color': ['黑', '白']})
df2 = pd.DataFrame({'Age': [10, 10]})
df_concat = pd.concat([df1, df2], axis=1)
print('df1=')
print(df2)
print()
print('df2=')
print(df2)
print()
print('列合并结果为')
print('df_concat=')
print(df_concat)
df1=
Age
0 10
1 10
df2=
Age
0 10
1 10
列合并结果为
df_concat=
name color Age
0 小黑 黑 10
1 小白 白 10
copy函数
copy函数的参数deep=False时为浅复制,deep=True时为深复制。原来网上是说deep=False为默认值,但是个人实践发现,在python3.8版本下,deep=True为默认值。
import pandas as pd
df = pd.DataFrame({'a':[1, 2], 'b':[3, 4]})
print('原来df=')
print(df)
print('然后用不同方式复制df....然后更改df.....')
df_True = df.copy(deep=True)
df_False = df.copy(deep=False)
df_Default = df.copy()
df['a'][0] = 10
print('更改后的df=')
print(df)
print('深复制得到df_True=')
print(df_True)
print('浅复制得到df_False=')
print(df_False)
print('默认复制(深复制)的得到的df_Default=')
print(df_Default)
原来df=
a b
0 1 3
1 2 4
然后用不同方式复制df....然后更改df.....
更改后的df=
a b
0 10 3
1 2 4
深复制得到df_True=
a b
0 1 3
1 2 4
浅复制得到df_False=
a b
0 10 3
1 2 4
默认复制(深复制)的得到的df_Default=
a b
0 1 3
1 2 4