Description
在xoy直角坐标平面上有n条直线L1,L2,...Ln,若在y值为正无穷大处往下看,能见到Li的某个子线段,则称Li为可见的,否则Li为被覆盖的.
例如,对于直线: L1:y=x; L2:y=-x; L3:y=0 则L1和L2是可见的,L3是被覆盖的.
给出n条直线,表示成y=Ax+B的形式(|A|,|B|<=500000),且n条直线两两不重合.求出所有可见的直线.
Input
第一行为N(0 < N < 50000),接下来的N行输入Ai,Bi
Output
从小到大输出可见直线的编号,两两中间用空格隔开,最后一个数字后面也必须有个空格
Sample Input
3
-1 0
1 0
0 0
-1 0
1 0
0 0
Sample Output
1 2
按照k排序,然后就可以维护一个栈,从斜率小的直线往斜率大的直线扫,栈中都是目前可见直线。
每扫到一个直线,就看栈顶直线是否已经被全部覆盖(被当前直线挡住的右部分的左端点在它被挡住的最大左部分的右端点左边),如果已经被全部覆盖,就弹栈,一直到栈顶直线不会被覆盖,这时的栈顶直线就会是挡住当前直线最大左部分的直线。然后把当前直线放入栈中。最后栈中直线就是可见直线。
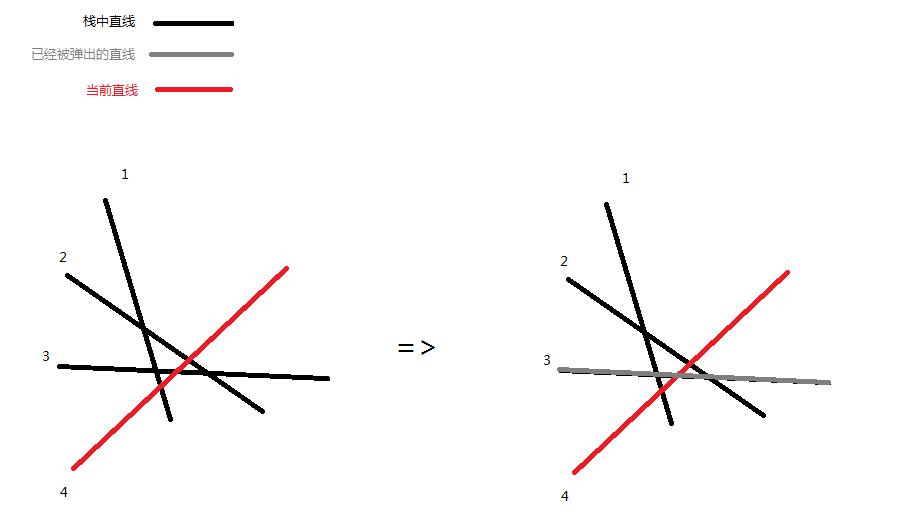
啊。。。我到底在说什么。。。直接上代码。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn=50000+10;
int n,zz[maxn],e=0;
int aa,fl;char cc;
int read() {
aa=0;cc=getchar();fl=1;
while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
if(cc=='-') fl=-1,cc=getchar();
while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
return aa*fl;
}
struct Node{
int k,b,pos;
}node[maxn];
bool cmp(const Node& x,const Node& y) {
return x.k==y.k? x.b>y.b : x.k<y.k;
}
double px(int x,int y){
return 1.0*(double)(node[y].b-node[x].b)/(double)(node[x].k-node[y].k);
}
bool ok(int x,int y,int z) {
return (double)px(x,y)>=(double)px(y,z);//每条直线的最大被挡左部分的右端点一定是栈中的排在它前面的上一条直线与它的交点
}
int main() {
n=read();
for(int i=1;i<=n;++i) {
node[i].pos=i;
node[i].k=read();
node[i].b=read();
}
sort(node+1,node+n+1,cmp);
for(int i=1;i<=n;++i) if(e==0||node[i].k!=node[zz[e]].k){
while(e>1&&ok(zz[e-1],zz[e],i)) e--;
zz[++e]=i;
}
for(int i=1;i<=e;++i) zz[i]=node[zz[i]].pos;
sort(zz+1,zz+e+1);
for(int i=1;i<=e;++i) printf("%d ",zz[i]);
return 0;
}