CQOI2018

和SCOI2018形成鲜明对比……

板子题+大力卡常。

作为大常数选手的我被卡得瑟瑟发抖。

发现自己板子还是不熟，常数还是太大，智障错误还是太多

D1T1

BSGS

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<map>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
ll n,A,B,mod,g,f,sz,a,b;

map<ll,int> G;

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

ll qp(ll x,ll k) {
	ll rs=1;
	while(k) {
		if(k&1) rs=rs*x%mod;
		k>>=1; x=x*x%mod;
	}
	return rs;
}

ll get_ans(ll x) {
	if(x==1) return 0;
	For(i,0,mod) {
		if(x==1) return i*sz;
		if(G[x]) return i*sz+G[x];
		x=x*f%mod;
	}
}

int main() {
	freopen("crack.in","r",stdin);
	freopen("crack.out","w",stdout);
	read(g); read(mod); sz=sqrt(mod);
	ll x=1;
	For(i,1,sz) {
		x=x*g%mod;
		if(!G[x]) G[x]=i;
	}
	f=qp(x,mod-2);
	read(n);
	For(i,1,n) {
		read(A); read(B);
		a=get_ans(A);
		b=get_ans(B);
		printf("%lld
",qp(g,a*b));
	}
	return 0;
}

D1T2

Matrix Tree定理

今天早读的时候在打这个板子，然后WA了还没调出来，又遇到这道题，和早上WA的地方一模一样

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const ll mod=10007,maxn=500+7,maxm=maxn*maxn;
int n,m,id[maxn],tot;
ll D[maxn][maxn];

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

int fir[maxn],nxt[maxm],to[maxm],e=0;
void add(int x,int y) {
	to[++e]=y;nxt[e]=fir[x];fir[x]=e;
}

bool vis[maxn];
void s(int pos) {
	if(vis[pos]) return;
	vis[pos]=1;
	for(int y=fir[pos];y;y=nxt[y]) s(to[y]);
}

void insert(int x,int y) {
	D[x][y]--;
//	D[y][x]--;
	D[y][y]++;
}

ll Mtx(int n) {
	ll a,b,r,rs=1,fl=0;
	For(i,1,n) For(j,1,n) D[i][j]=(D[i][j]+mod)%mod;
	For(i,1,n) {
		For(j,i+1,n) if(D[j][i]) {
			a=D[i][i]; b=D[j][i];
			while(b) {
				r=a/b; a=a%b; swap(a,b);
				For(k,i,n) D[i][k]=(D[i][k]-D[j][k]*r%mod+mod)%mod;
				swap(D[i],D[j]);
				fl^=1;
			}
		}
		if(D[i][i]==0) return 0;
		rs=rs*D[i][i]%mod;
	}
	if(fl) rs=(mod-rs)%mod;
	return rs;
}

int main() {
	freopen("sns.in","r",stdin);
	freopen("sns.out","w",stdout);
	read(n); read(m);
	int x,y;
	For(i,1,m) {
		read(x); read(y);
		add(y,x);
	}
	s(1);
	Rep(i,n,1) if(vis[i]) 
		id[i]=++tot;
	For(i,1,n) if(vis[i]) 
		for(y=fir[i];y;y=nxt[y]) if(vis[to[y]])
			insert(id[i],id[to[y]]);
	printf("%lld
",Mtx(tot-1));
	return 0;
}

D1T3

不晓得正解是什么，我枚举1的个数然后用组合数直接算，被卡常卡得我妈都不认识了

然后用llj的优化方法，线筛预处理i^a和i^b，还是卡常。

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(register int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(register int i=(a);i>=(b);--i)
const int maxn=1e7+7;
ll n,W,a,b,mod,mi[maxn],inv[maxn],sum[maxn],p1[maxn],p2[maxn],ans,x,y;
ll num[maxn];

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

inline ll qp(ll x,ll k) {
	ll rs=1;
	while(k) {
		if(k&1) rs=rs*x%mod;
		k>>=1; x=x*x%mod;
	}
	return rs;
}

int prime[maxn],totp;
bool ok[maxn];
inline void get_p() {
	p1[0]=a==0;
	p2[0]=b==0; 
	p1[1]=p2[1]=1;
	For(i,2,W) {
		if(!ok[i]) {
			p1[i]=qp(i,a);
			p2[i]=qp(i,b);
			prime[++totp]=i;
		} 
		For(j,1,totp) {
			if(prime[j]*i>W) break;
			ok[i*prime[j]]=1;
			p1[i*prime[j]]=p1[i]*p1[prime[j]]%mod;
			p2[i*prime[j]]=p2[i]*p2[prime[j]]%mod;
			if(i%prime[j]==0) break;
		}
	}
}

inline ll C(ll n,ll m) {
	if(sum[n]-sum[m]-sum[n-m]>0) return 0;
	return mi[n]*inv[m]%mod*inv[n-m]%mod;
}

int main() {
	freopen("seq.in","r",stdin);
	freopen("seq.out","w",stdout);
	read(n); read(a); read(b); read(mod);
	W=n+3;
	get_p();
//	cerr<<clock()<<"
";
	mi[0]=1;
	x=mod; while(x<=W) num[x]=1,x+=mod;
	For(i,1,W) {
		if(num[i]) sum[i]=sum[i/mod]+1,num[i]=num[i/mod];
		else num[i]=i;
		mi[i]=mi[i-1]*num[i]%mod;
	}
	For(i,1,W) sum[i]+=sum[i-1];
	inv[W]=qp(mi[W],mod-2);
	Rep(i,W,1) 
		inv[i-1]=inv[i]*num[i]%mod;
//	cerr<<clock()<<"
";
	For(i,0,(n+1)>>1) {//tot of 1
		x=n-i; //tot of 0
		y=x-(i-1); //remain of 0
		ans+=p1[x]*p2[i]%mod*C(y+i,y)%mod;
	} 
	printf("%lld
",ans%mod);
//	cerr<<clock()<<"
";
	return 0;
}

D2T1

 

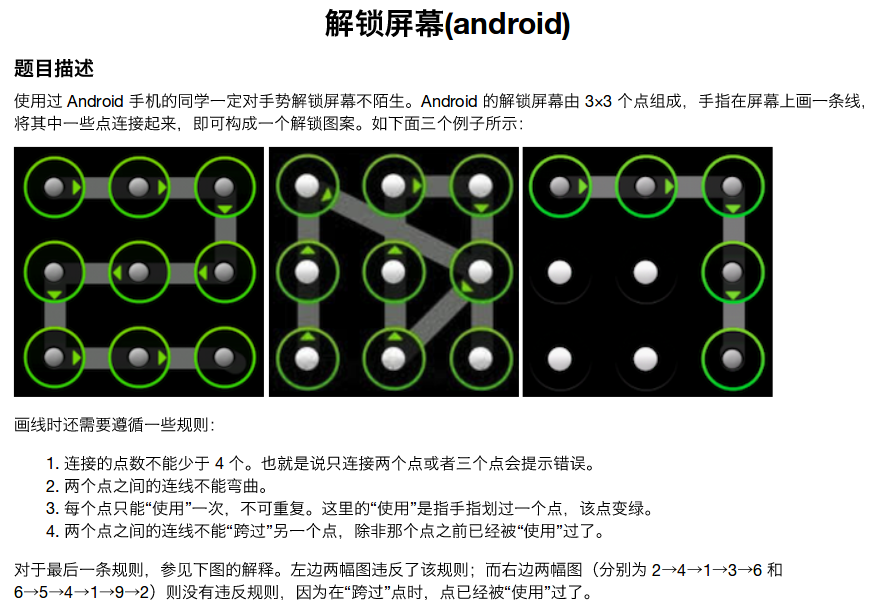
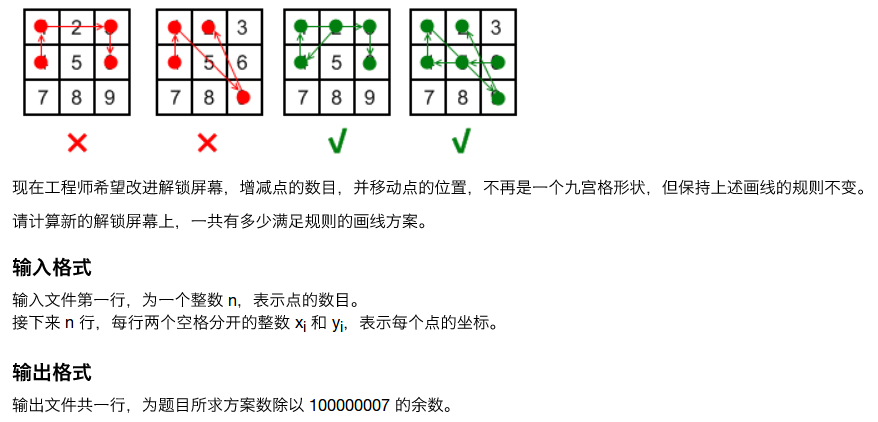
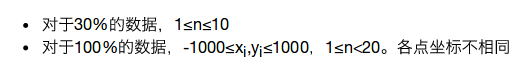
状压dp，我的记忆化搜索可以被卡60分的常？

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=23,maxt=(1<<19)+7;
const ll mod=1e8+7;
ll n,W,f[maxt][maxn],nd[maxn][maxn],cnt[maxt],ans;

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

struct Xl{
	ll x,y;
	Xl(db x=0.,db y=0.):x(x),y(y){}
	Xl operator + (const Xl& b) const{return Xl(x+b.x,y+b.y);}
	Xl operator - (const Xl& b) const{return Xl(x-b.x,y-b.y);}
}p[maxn];

ll X_(const Xl& a,const Xl& b) {return a.x*b.y-a.y*b.x;}
ll D_(const Xl& a,const Xl& b) {return a.x*b.x+a.y*b.y;}

bool onit(const Xl& o,const Xl& a,const Xl& b) {
	if(X_(o-a,b-a)!=0) return 0;
	if(D_(o-a,b-a)<0) return 0;
	if(D_(o-b,a-b)<0) return 0;
	return 1;
}

int main() {
	freopen("android.in","r",stdin);
	freopen("android.out","w",stdout);
	read(n); W=(1<<n)-1;
	ll x,y;
	For(i,1,n) {
		read(x); read(y);
		p[i]=Xl(x,y);
	}
	For(i,1,n) For(j,i+1,n) {
		For(k,1,n) if(k!=i&&k!=j)
			if(onit(p[k],p[i],p[j])) nd[i][j]|=(1<<k-1);
		nd[j][i]=nd[i][j];
	}
	For(i,1,W) cnt[i]=cnt[i-(i&-i)]+1;
	For(i,1,n) f[1<<i-1][i]=1;
	For(i,0,W) For(j,1,n) if(f[i][j]%=mod) {
		For(k,1,n) if((i&(1<<k-1))==0&&(nd[j][k]&i)==nd[j][k]) 
			f[i|(1<<k-1)][k]+=f[i][j];
	}
	For(i,0,W) if(cnt[i]>3) For(j,1,n) ans+=f[i][j];	
	printf("%lld
",ans%mod);
//	cerr<<clock()<<"
";
	return 0;
}

D2T2

家里有九连环，总觉得自己手速太慢，思考过这个问题，但是当时没思考出来（毕竟当时还没学OI）。

打表可知:

i为奇数的时候，f[i]=f[i-1]<<1|1

i为偶数的时候，f[i]=f[i-1]<<1

需要高精，似乎Achen被卡常了

我场上写输出的时候0的个数不太对，WA惨了

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=2000+7,maxt=103;
ll Td,n,now[maxn],ans[maxt][maxn],W=1e18,q[maxt];

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

void qc() {
	For(i,1,now[0]) now[i]<<=1;
	For(i,1,now[0]) while(now[i]>=W) now[i]-=W,now[i+1]++;
	if(now[now[0]+1]) now[0]++;
}

void qj() {
	now[1]++;
	ll pos=1;
	while(now[pos]>=W) now[pos]-=W,now[++pos]++;
	now[0]=max(now[0],pos);
}

void print_ans(ll* now) {
	printf("%lld",now[now[0]]);
	Rep(i,now[0]-1,1) printf("%018lld",now[i]);
	printf("
");
}

int main() {
	freopen("baguenaudier.in","r",stdin);
	freopen("baguenaudier.out","w",stdout);
	read(Td);
	For(i,1,Td) read(q[i]),q[0]=max(q[0],q[i]);
	n=q[0];
	memset(now,0,sizeof(now));
	now[0]=1;
	For(i,1,n) {
		qc();
		if(i&1) qj();
		For(j,1,Td) if(q[j]==i) memcpy(ans[j],now,sizeof(now));
	}
	For(i,1,Td) print_ans(ans[i]);
//		cerr<<clock()<<"
";
	return 0;
}

D2T3

莫队

一开始以为每次查询的k互不相同，要动态维护线性基，所以写了一个回滚莫队……

然后懒得改成普通莫队了

//Serene
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
using namespace std;
#define ll long long
#define db double
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rep(i,a,b) for(int i=(a);i>=(b);--i)
const int maxn=5e5+7;
ll n,m,K,a[maxn],ans[maxn],sz;

char cc; ll ff;
template<typename T>void read(T& aa) {
	aa=0;cc=getchar();ff=1;
	while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
	if(cc=='-') ff=-1,cc=getchar();
	while(cc>='0'&&cc<='9') aa=aa*10+cc-'0',cc=getchar();
	aa*=ff;
}

int id(int x) {return x/sz;}

struct Ask{
	int l,r,qid;
	Ask(){}
	Ask(int l,int r,int qid):l(l),r(r),qid(qid){}
	bool operator < (const Ask& b) const{return id(l)==id(b.l)? r<b.r:l<b.l;}
}ask[maxn];
int tot;

ll sum[maxn],now,nw;
int mdf[maxn],cnt;

void clear() {
	while(cnt) --sum[mdf[cnt--]];
	now-=nw; nw=0;
}

void clear_all() {
	memset(sum,0,sizeof(sum));
	cnt=now=nw=0;
}

void insert(int x,int o) {
	if(o) mdf[++cnt]=x,nw+=sum[x^K];
	now+=sum[x^K];
	++sum[x];
}

void solve(int l,int r,int p) {
	For(i,l,r) insert(a[i],1);
	ans[p]=now;
	clear();
}

int main() {
	freopen("xor.in","r",stdin);
	freopen("xor.out","w",stdout);
	read(n); read(m); read(K);
	For(i,1,n) read(a[i]),a[i]^=a[i-1]; 
	sz=sqrt(n);
	int l,r;
	For(i,1,m) {
		read(l); read(r);
		if(r-l<=2*sz) solve(l-1,r,i);
		else ask[++tot]=Ask(l-1,r,i);
	}
	sort(ask+1,ask+tot+1);
	int last=1,ld,rd;
	For(i,1,tot) {
		if(i==tot||id(ask[i].l)!=id(ask[i+1].l)) {
			clear_all();
			ld=rd=(id(ask[i].l)+1)*sz-1;
			For(j,last,i) {
				clear();
				For(k,rd+1,ask[j].r) insert(a[k],0);
				rd=ask[j].r;
				Rep(k,ld,ask[j].l) insert(a[k],1);
				ans[ask[j].qid]=now;
			}
			last=i+1;
		}
	}
	For(i,1,m) printf("%lld
",ans[i]);
	return 0;
}