Codeforces Global Round 6

Competitive Programmer

Bob is a competitive programmer. He wants to become red, and for that he needs a strict training regime. He went to the annual meeting of grandmasters and asked nn of them how much effort they needed to reach red.

"Oh, I just spent xixi hours solving problems", said the ii-th of them.

Bob wants to train his math skills, so for each answer he wrote down the number of minutes (60⋅xi60⋅xi), thanked the grandmasters and went home. Bob could write numbers with leading zeroes — for example, if some grandmaster answered that he had spent 22 hours, Bob could write 000120000120 instead of 120120.

Alice wanted to tease Bob and so she took the numbers Bob wrote down, and for each of them she did one of the following independently:

• rearranged its digits, or
• wrote a random number.

This way, Alice generated nn numbers, denoted y1y1, ..., ynyn.

For each of the numbers, help Bob determine whether yiyi can be a permutation of a number divisible by 6060 (possibly with leading zeroes).

Input

The first line contains a single integer nn (1≤n≤4181≤n≤418) — the number of grandmasters Bob asked.

Then nn lines follow, the ii-th of which contains a single integer yiyi — the number that Alice wrote down.

Each of these numbers has between 22 and 100100 digits '0' through '9'. They can contain leading zeroes.

Output

Output nn lines.

For each ii, output the following. If it is possible to rearrange the digits of yiyi such that the resulting number is divisible by 6060, output "red" (quotes for clarity). Otherwise, output "cyan".

Example

input

Copy

6
603
006
205
228
1053
0000000000000000000000000000000000000000000000

output

Copy

red
red
cyan
cyan
cyan
red

Note

In the first example, there is one rearrangement that yields a number divisible by 6060, and that is 360360.

In the second example, there are two solutions. One is 060060 and the second is 600600.

In the third example, there are 66 possible rearrangments: 025025, 052052, 205205, 250250, 502502, 520520. None of these numbers is divisible by 6060.

In the fourth example, there are 33 rearrangements: 228228, 282282, 822822.

In the fifth example, none of the 2424 rearrangements result in a number divisible by 6060.

In the sixth example, note that 000…0000…0 is a valid solution.

 

 

 #include <bits/stdc++.h>
using namespace std;
int vis[11];
int n,m,t;
string str;
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>str;
        int ans = 0;
        memset(vis,0,sizeof(vis));
        for(int i=0; i<str.size(); i++)
            vis[ str[i]-'0' ]++;
        for(int i=1; i<=9; i++)
            ans += i*vis[i];
        
        
        if(vis[0]==str.size())
            cout<<"red"<<endl;
        else if(ans%3!=0)
            cout<<"cyan"<<endl;
        else if(vis[0])
        {
            vis[0]--;
            if( vis[2] || vis[4] || vis[6] || vis[8] || vis[0] )
                cout<<"red"<<endl;
            else
                cout<<"cyan"<<endl;
        }
        else
            cout<<"cyan"<<endl;
    }
}

Dice Tower

Bob is playing with 66-sided dice. A net of such standard cube is shown below.

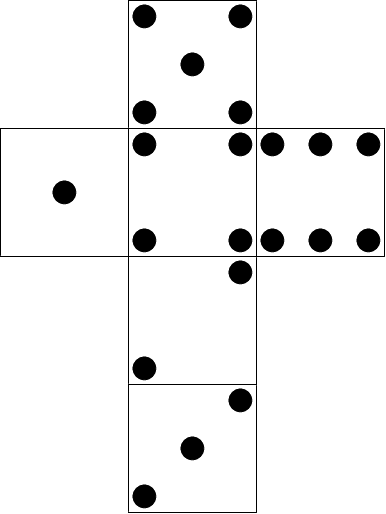
He has an unlimited supply of these dice and wants to build a tower by stacking multiple dice on top of each other, while choosing the orientation of each dice. Then he counts the number of visible pips on the faces of the dice.

For example, the number of visible pips on the tower below is 2929 — the number visible on the top is 11, from the south 55 and 33, from the west 44 and 22, from the north 22 and 44 and from the east 33 and 55.

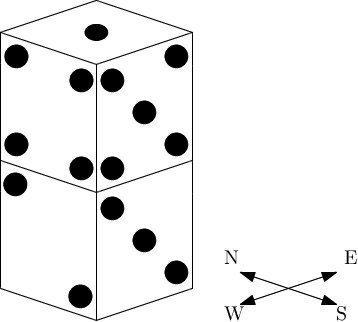
The one at the bottom and the two sixes by which the dice are touching are not visible, so they are not counted towards total.

Bob also has tt favourite integers xixi, and for every such integer his goal is to build such a tower that the number of visible pips is exactly xixi. For each of Bob's favourite integers determine whether it is possible to build a tower that has exactly that many visible pips.

Input

The first line contains a single integer tt (1≤t≤10001≤t≤1000) — the number of favourite integers of Bob.

The second line contains tt space-separated integers xixi (1≤xi≤10181≤xi≤1018) — Bob's favourite integers.

Output

For each of Bob's favourite integers, output "YES" if it is possible to build the tower, or "NO" otherwise (quotes for clarity).

Example

input

Copy

4
29 34 19 38

output

Copy

YES
YES
YES
NO

Note

The first example is mentioned in the problem statement.

In the second example, one can build the tower by flipping the top dice from the previous tower.

In the third example, one can use a single die that has 55 on top.

The fourth example is impossible.

#include <bits/stdc++.h>
using namespace std;
int vis[1000+10],a[]={20,19,18,17,16,15};
long long  n,m,t;
string str;
int main()
{   
    cin>>t;
    while(t--)
    {
        cin>>n;
        if(n<15)
            cout<<"NO"<<endl;
        
        else if(n%14<=6 && n%14>0)
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
}

Diverse Matrix

Let aa be a matrix of size r×cr×c containing positive integers, not necessarily distinct. Rows of the matrix are numbered from 11 to rr, columns are numbered from 11 to cc. We can construct an array bb consisting of r+cr+c integers as follows: for each i∈[1,r]i∈[1,r], let bibi be the greatest common divisor of integers in the ii-th row, and for each j∈[1,c]j∈[1,c] let br+jbr+j be the greatest common divisor of integers in the jj-th column.

We call the matrix diverse if all r+cr+c numbers bkbk (k∈[1,r+c]k∈[1,r+c]) are pairwise distinct.

The magnitude of a matrix equals to the maximum of bkbk.

For example, suppose we have the following matrix:

(249144784)(297414484)

We construct the array bb:

1. b1b1 is the greatest common divisor of 22, 99, and 77, that is 11;
2. b2b2 is the greatest common divisor of 44, 144144, and 8484, that is 44;
3. b3b3 is the greatest common divisor of 22 and 44, that is 22;
4. b4b4 is the greatest common divisor of 99 and 144144, that is 99;
5. b5b5 is the greatest common divisor of 77 and 8484, that is 77.

So b=[1,4,2,9,7]b=[1,4,2,9,7]. All values in this array are distinct, so the matrix is diverse. The magnitude is equal to 99.

For a given rr and cc, find a diverse matrix that minimises the magnitude. If there are multiple solutions, you may output any of them. If there are no solutions, output a single integer 00.

Input

The only line in the input contains two space separated integers rr and cc (1≤r,c≤5001≤r,c≤500) — the number of rows and the number of columns of the matrix to be found.

Output

If there is no solution, output a single integer 00.

Otherwise, output rr rows. The ii-th of them should contain cc space-separated integers, the jj-th of which is ai,jai,j — the positive integer in the ii-th row and jj-th column of a diverse matrix minimizing the magnitude.

Furthermore, it must hold that 1≤ai,j≤1091≤ai,j≤109. It can be shown that if a solution exists, there is also a solution with this additional constraint (still having minimum possible magnitude).

Examples

input

Copy

2 2

output

Copy

4 12
2 9

input

Copy

1 1

output

Copy

0

Note

In the first example, the GCDs of rows are b1=4b1=4 and b2=1b2=1, and the GCDs of columns are b3=2b3=2 and b4=3b4=3. All GCDs are pairwise distinct and the maximum of them is 44. Since the GCDs have to be distinct and at least 11, it is clear that there are no diverse matrices of size 2×22×2 with magnitude smaller than 44.

In the second example, no matter what a1,1a1,1 is, b1=b2b1=b2 will always hold, so there are no diverse matrices.

#include <iostream>
#include <cmath>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3
using namespace std;
const int mxn = 50000+10;
#define TLE std::ios::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#define ls now<<1,l,mid
#define rs now<<1|1,mid+1,r
#define lc now<<1
#define rc now<<1|1
#define upsum(now) rt[now].sum =rt[now<<1].sum + rt[now<<1|1].sum ;
#define upmx(now) rt[now].mx = max(rt[now<<1].mx , rt[now<<1|1].mx) ;
ll n,m,k,t,mx,mn,l,r,dp[mxn];
string str;
 
int main()
{
    TLE;
    while(cin>>n>>m)
    {
        if(n==1 && m==1)
            cout<<0<<endl;
        else
        {
            if(n>=m)
            {
                for(int i=1;i<=n;i++)
                {
                    for(int j=1;j<=m;j++)
                        cout<<(i+m)*j<<" ";
                    cout<<endl;
                }
            }
            else
                for(int i=1;i<=n;i++)
                {
                    for(int j=1;j<=m;j++)
                        cout<<(j+n)*i<<" ";
                    cout<<endl;
                }
        }
    }
    return 0;
}

Decreasing Debts

There are nn people in this world, conveniently numbered 11 through nn. They are using burles to buy goods and services. Occasionally, a person might not have enough currency to buy what he wants or needs, so he borrows money from someone else, with the idea that he will repay the loan later with interest. Let d(a,b)d(a,b) denote the debt of aa towards bb, or 00 if there is no such debt.

Sometimes, this becomes very complex, as the person lending money can run into financial troubles before his debtor is able to repay his debt, and finds himself in the need of borrowing money.

When this process runs for a long enough time, it might happen that there are so many debts that they can be consolidated. There are two ways this can be done:

1. Let d(a,b)>0d(a,b)>0 and d(c,d)>0d(c,d)>0 such that a≠ca≠c or b≠db≠d. We can decrease the d(a,b)d(a,b) and d(c,d)d(c,d) by zz and increase d(c,b)d(c,b) and d(a,d)d(a,d) by zz, where 0<z≤min(d(a,b),d(c,d))0<z≤min(d(a,b),d(c,d)).
2. Let d(a,a)>0d(a,a)>0. We can set d(a,a)d(a,a) to 00.

The total debt is defined as the sum of all debts:

Σd=∑a,bd(a,b)Σd=∑a,bd(a,b)

Your goal is to use the above rules in any order any number of times, to make the total debt as small as possible. Note that you don't have to minimise the number of non-zero debts, only the total debt.

Input

The first line contains two space separated integers nn (1≤n≤1051≤n≤105) and mm (0≤m≤3⋅1050≤m≤3⋅105), representing the number of people and the number of debts, respectively.

mm lines follow, each of which contains three space separated integers uiui, vivi (1≤ui,vi≤n,ui≠vi1≤ui,vi≤n,ui≠vi), didi (1≤di≤1091≤di≤109), meaning that the person uiui borrowed didi burles from person vivi.

Output

On the first line print an integer m′m′ (0≤m′≤3⋅1050≤m′≤3⋅105), representing the number of debts after the consolidation. It can be shown that an answer always exists with this additional constraint.

After that print m′m′ lines, ii-th of which contains three space separated integers ui,vi,diui,vi,di, meaning that the person uiui owes the person viviexactly didi burles. The output must satisfy 1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi and 0<di≤10180<di≤1018.

For each pair i≠ji≠j, it should hold that ui≠ujui≠uj or vi≠vjvi≠vj. In other words, each pair of people can be included at most once in the output.

Examples

input

Copy

3 2
1 2 10
2 3 5

output

Copy

2
1 2 5
1 3 5

input

Copy

3 3
1 2 10
2 3 15
3 1 10

output

Copy

1
2 3 5

input

Copy

4 2
1 2 12
3 4 8

output

Copy

2
1 2 12
3 4 8

input

Copy

3 4
2 3 1
2 3 2
2 3 4
2 3 8

output

Copy

1
2 3 15

Note

In the first example the optimal sequence of operations can be the following:

1. Perform an operation of the first type with a=1a=1, b=2b=2, c=2c=2, d=3d=3 and z=5z=5. The resulting debts are: d(1,2)=5d(1,2)=5, d(2,2)=5d(2,2)=5, d(1,3)=5d(1,3)=5, all other debts are 00;
2. Perform an operation of the second type with a=2a=2. The resulting debts are: d(1,2)=5d(1,2)=5, d(1,3)=5d(1,3)=5, all other debts are 00.

In the second example the optimal sequence of operations can be the following:

1. Perform an operation of the first type with a=1a=1, b=2b=2, c=3c=3, d=1d=1 and z=10z=10. The resulting debts are: d(3,2)=10d(3,2)=10, d(2,3)=15d(2,3)=15, d(1,1)=10d(1,1)=10, all other debts are 00;
2. Perform an operation of the first type with a=2a=2, b=3b=3, c=3c=3, d=2d=2 and z=10z=10. The resulting debts are: d(2,2)=10d(2,2)=10, d(3,3)=10d(3,3)=10, d(2,3)=5d(2,3)=5, d(1,1)=10d(1,1)=10, all other debts are 00;
3. Perform an operation of the second type with a=2a=2. The resulting debts are: d(3,3)=10d(3,3)=10, d(2,3)=5d(2,3)=5, d(1,1)=10d(1,1)=10, all other debts are 00;
4. Perform an operation of the second type with a=3a=3. The resulting debts are: d(2,3)=5d(2,3)=5, d(1,1)=10d(1,1)=10, all other debts are 00;
5. Perform an operation of the second type with a=1a=1. The resulting debts are: d(2,3)=5d(2,3)=5, all other debts are 00.