数据结构

数据结构和算法概念

数据结构的定义

​ 我们如何把现实中大量而且非常复杂的问题以特定的数据类型(个体)和特定的存储结构(个体的关系)保存到相应的主存储器(内存)中，以及在此基础上为实现某个功能而执行的相应操作，这个相应的操作也叫做算法。

数据结构 == 个体 + 个体的关系

算法 == 对存储数据的操作

数据结构的特点

数据结构是软件中最核心的课程

程序 = 数据的存储 + 数据的操作 + 可以被计算机执行的语言

算法

衡量算法的标准

• 时间复杂度 指的是大概程序执行的次数，而非程序执行的时间
• 空间复杂度 指的是程序执行过程中，大概所占有的最大内存
• 难易程度
• 健壮性

常见的几个排序:

• 冒泡排序
• 选择排序
• 插入排序
• 快速排序
• 归并排序
• 计数排序

常见的查找:

• 顺序查找
• 二分查找

应用场景:

• 各种榜单
• 各种表格
• 给二分查找用
• 给其他算法用

算法的思想:

• 穷举法 brute force
• 分治法 divide conquer
• 模拟
• 递归
• 贪心
• 动态规划

线性结构

把所有的节点用一根线串起来

数据的链表的区别

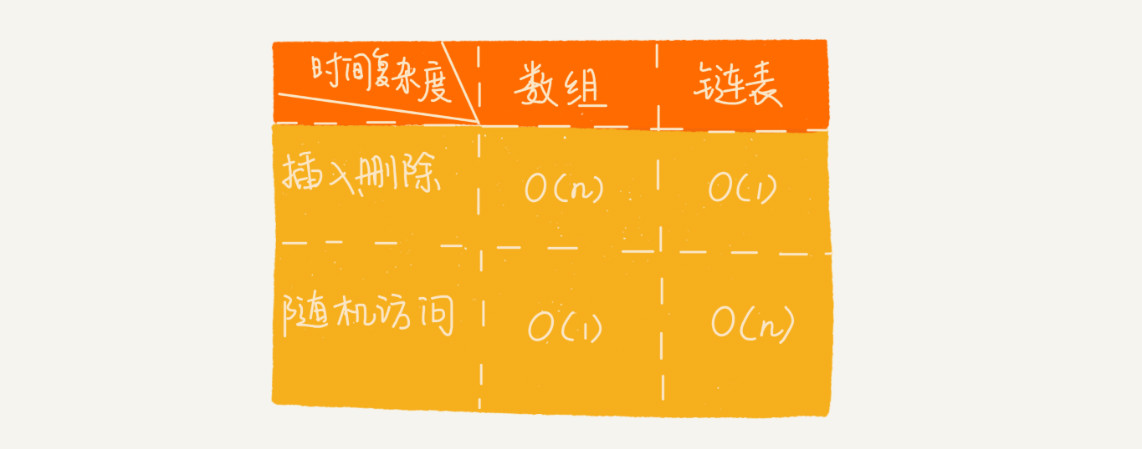
​ 数组需要一块连续的内存空间来存储，对内存的要求比较高。如果我们申请一个 100MB 大小的数组，当内存中没有连续的、足够大的存储空间时，即便内存的剩余总可用空间大于 100MB，仍然会申请失败。 而链表恰恰相反，它并不需要一块连续的内存空间,它通过“指针”将一组零散的内存块串联起来使用，所以如果我们申请的是 100MB 大小的链表，根本不会有问题。

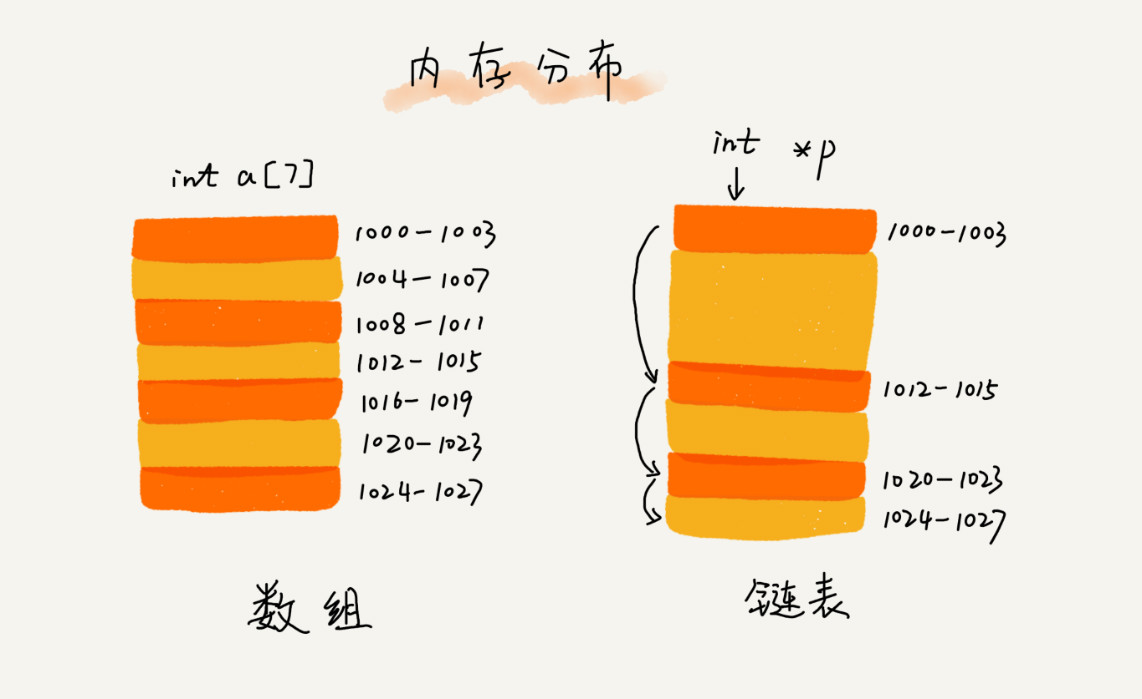
连续存储(数组)

​ 数组，在其python语言中称为列表，是一种基本的数据结构类型

关于列表的问题：

• 数组(列表)中的元素是如何存储的
• 列表提供了哪些最基本的操作？
• 这些操作的时间复杂度是多少？
• 为什么数组(列表)的索引或者下标是从0开始？

关于数组(列表)的优缺点:

• 优点:
  • 存取速度快
• 缺点：
  • 事先需要知道数组的长度
  • 需要大块的连续内存
  • 插入删除非常的慢，效率极低

离散存储(链表)

1.定义:

• n个节点离散分配
• 彼此通过指针相连
• 每个节点只有一个前驱节点，每个节点只有一个后续节点
• 首节点没有前驱节点，尾节点没有后续节点

优点

空间没有限制，插入删除元素很快

缺点

查询比较慢

链表的节点的结构如下:

值	指针域
data	next

data为自定义的数据，next为下一个节点的地址。

2.专业术语

• 首节点：第一个有效节点
• 尾节点：最后一个有效节点
• 头结点：第一个有效节点之前的那个节点，头结点并不存储任何数据，目的是为了方便对链表的操作
• 头指针：指向头结点的指针变量
• 尾指针：指向尾节点的指针变量

3.链表的分类

• 单链表
• 双链表 每一个节点有两个指针域
• 循环链表 能通过任何一个节点找到其他所有的节点
• 非循环链表

4.算法

• 增加
• 删除
• 修改
• 查找
• 总长度

有一堆数据1,2,3,5,6,7我们要在3和5之间插入4,如果用数组，我们会怎么做？当然是将5之后的数据往后退一位，然后再插入4,这样非常麻烦，但是如果用链表，我就直接在3和5之间插入4就行，听着就很方便

5.如果希望通过一个函数来对链表进行处理操作，至少需要接受链表的哪些参数？

只需要一个参数，头节点即可，因为我们可以通过头节点来推算出链表的其他所有的参数

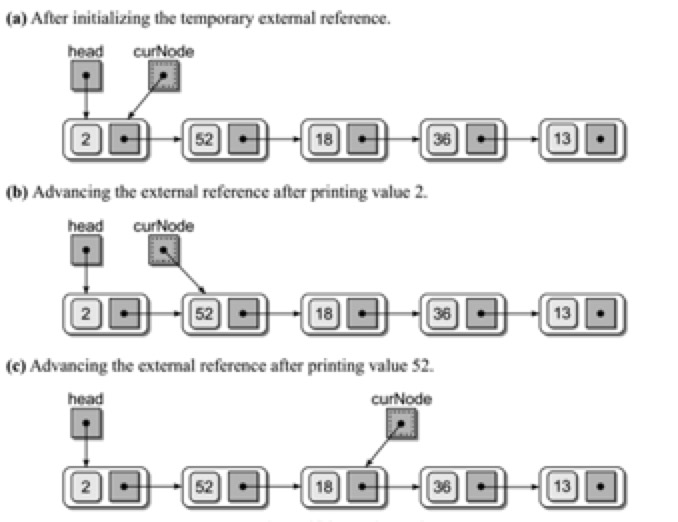
6.单链表的算法

class Hero(object):
    def __init__(self, no=0, name="", nickname="", pNext=None):
        self.no = no
        self.name = name
        self.nickname = nickname
        self.pNext = pNext
def getHero(head, no):
    cur = head
    while cur.pNext != None:
        if cur.no == no:
            print("找到的英雄的编号是： %s，姓名是：%s，外号是：%s" % (cur.no, cur.name, cur.nickname))
            break
        cur = cur.pNext
    else:
        print("没有这个英雄")
def add(head, hero):
    # 1. 直接在链表的最后加上
    # 先找到链表的最后
    cur = head
    # while cur.pNext != None:
    #     cur = cur.pNext
    # # 当退出链表的时候，就算是队尾了
    # cur.pNext = hero
    # 2. 指定位置进行添加
    while cur.pNext != None:
        if cur.pNext.no >= hero.no:
            # 找到位置
            break
        # 继续往下走
        cur = cur.pNext
    hero.pNext = cur.pNext
    cur.pNext = hero
def showAll(head):
    cur = head
    while cur.pNext != None:
        print("英雄的编号是： %s，姓名是：%s，外号是：%s" % (cur.pNext.no,cur.pNext.name,cur.pNext.nickname))
        cur = cur.pNext
def delHero(head, no):
    cur = head
    while cur.pNext != None:
        if cur.pNext.no == no:
            # 开始删除
            cur.pNext = cur.pNext.pNext
            break
        cur = cur.pNext
    else:
        print('没有找到')
def updateHero(head, no, name):
    cur = head
    while cur.pNext != None:
        if cur.pNext.no == no:
            cur.pNext.name = name
            break
        cur = cur.pNext
    else:
        print('没有找到英雄')
def is_empty(head):
    if head.pNext == None:
        return True
    return False
def length(head):
    cnt = 0
    cur = head
    while cur.pNext != None:
        cnt = cnt + 1
        cur = cur.pNext
    return cnt
# 创建一个head头，该head只是一个头，不存放数据
head = Hero()
# print(is_empty(head))
hero = Hero(1, '宋江', '及时雨')
# head.pNext = hero
add(head, hero)
hero = Hero(2, '卢俊义', '玉麒麟')
# hero.pNext = hero2
add(head, hero)
hero = Hero(6, '林冲', '豹子头')
add(head, hero)
hero = Hero(3, '吴用', '智多星')
add(head, hero)
# 遍历所有的英雄
showAll(head)
# delHero(head, 3)
# print('删除之后的排列：')
updateHero(head,3,'张三')
print('###############修改之后的排列：################')
showAll(head)
print(length(head))
# getHero(head, 3)

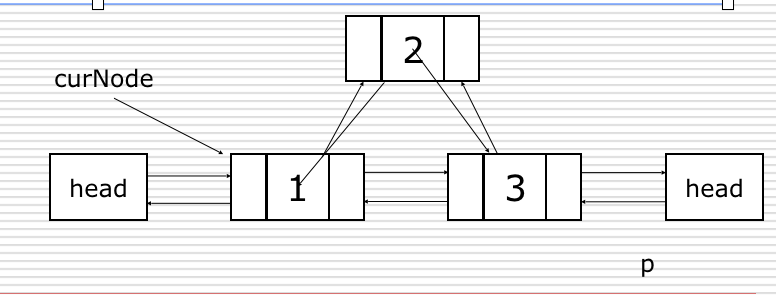
7.双向链表

​ 双链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点。

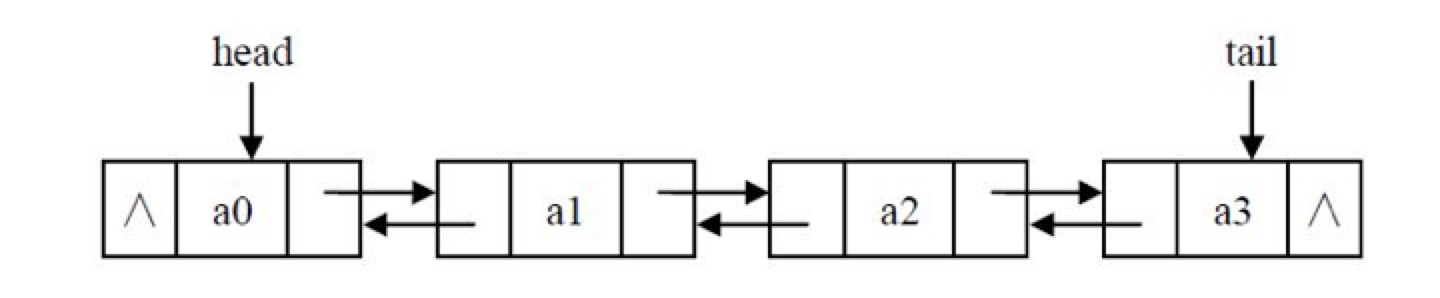
class Node(object):
    def __init__(self, data=None):
        self.data = data
        self.next = None
        self.prior = None

双向链表的操作:

插入:

p.next = curNode.next
curNode.next.prior = p
curNode.next = p
p.prior = curNode

删除:

p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p

8.循环链表

​ 循环链表是另一种形式的链式存贮结构。它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。

9.约瑟夫问题

​ 设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，直到所有人出列为止，由此产生一个出队编号的序列。

class Child(object):
    first = None

    def __init__(self, no=None, pNext=None):
        self.no = no
        self.pNext = pNext

    def addChild(self, n=4):
        cur = None
        for i in range(n):
            child = Child(i + 1)
            if i == 0:
                self.first = child
                self.first.pNext = child
                cur = self.first
            else:
                cur.pNext = child
                child.pNext = self.first
                cur = cur.pNext

    def showChild(self):
        cur = self.first
        while cur.pNext != self.first:
            print("小孩的编号是：%d" % cur.no)
            cur = cur.pNext
        print("小孩的编号是: %d" % cur.no)

    def countChild(self, m, k):
        tail = self.first
        while tail.pNext != self.first:
            tail = tail.pNext
        # 出来后，已经是在first前面
        # 从第几个人开始数
        for i in range(k - 1):
            tail = tail.pNext
            self.first = self.first.pNext
        # 数两下，就是让first和tail移动一次
        # 数三下，就是让first和tail移动两次
        while tail != self.first:  # 当tail == first 说明只剩一个人
            for i in range(m - 1):
                tail = tail.pNext
                self.first = self.first.pNext
            self.first = self.first.pNext
            tail.pNext = self.first
        print("最后留在圈圈中的人是：%d" % tail.no)


c = Child()
c.addChild(4)
c.showChild()
c.countChild(3, 2)

数组的链表的性能比较

线性结构的两种应用方式之栈

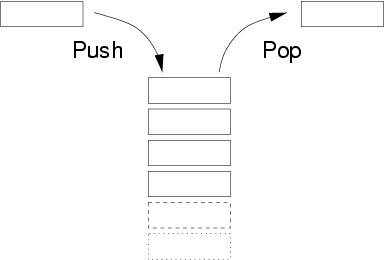
栈的定义

一种可以实现"先进后出"的存储结构

​ 栈类似于一个箱子，先放进去的书，最后才能取出来，同理，后放进去的书，先取出来。

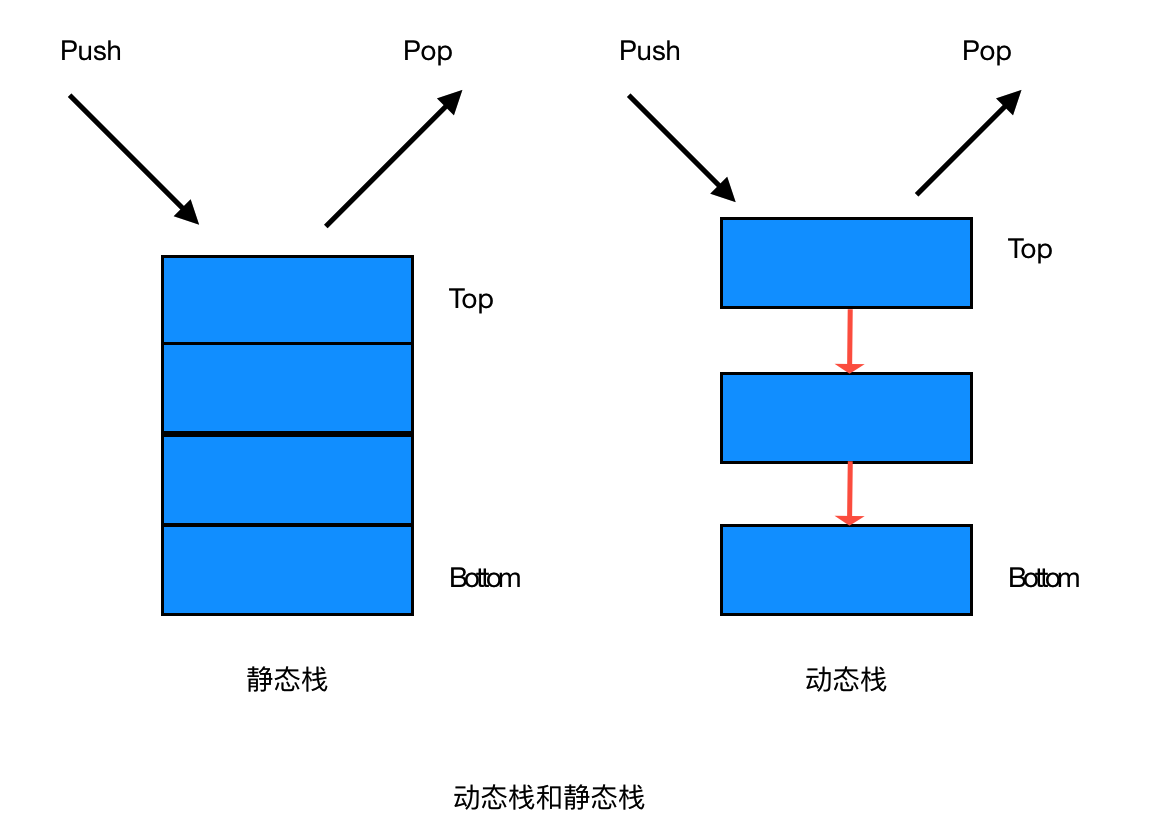
栈的分类

• 静态栈
  • 静态栈的核心是数组，类似于一个连续内存的数组，我们只能操作其栈顶元素
• 动态栈
  • 动态栈的核心是链表

栈的算法

​ 栈的算法主要是压栈和出栈两种操作的算法，下面我就用代码来实现一个简单的栈。

首先要明白以下思路：

• 栈操作的是一个一个节点
• 栈本身也是一种存储的数据结构
• 栈有初始化、压栈、出栈、判空、遍历、清空等主要方法

class Stack(object):
    def __init__(self):
        self.pTop = None
        self.pBottom = None
class Node(object):
    def __init__(self, data=None, pNext = None):
        self.data = data
        self.pNext = pNext
def push(s, new):
    new.pNext = s.pTop
    s.pTop = new
def pop(s):
    cur = s.pTop
    # while cur != s.pBottom:
    #     if cur.data == val:
    #         s.pTop = cur.pNext
    #         break
    #     cur = cur.pNext
    # else:
    #     print('没有找到此元素')
    while cur != s.pBottom:
        s.pTop = cur.pNext
        print("出栈的元素是: %d" % cur.data)
        cur = cur.pNext
    else:
        print("出栈失败")
def getAll(s):
    cur = s.pTop
    while cur != s.pBottom:
        print(cur.data)
        cur = cur.pNext
def is_empty(s):
    if s.pTop == s.pBottom:
        return True
    else:
        return False
def clear(s):
    if is_empty(s):
        return None
    p = s.pTop
    q = None
    while p != s.pBottom:
        q = p.pNext
        del p
        p = q
    else:
        s.pBottom = s.pTop
head = Node()
s = Stack()
s.pTop = s.pBottom = head
n1 = Node(2)
push(s, n1)
n1 = Node(5)
push(s, n1)
n1 = Node(89)
push(s, n1)
print("##############遍历元素##########")
getAll(s)
# print("##############出栈元素#######")
# pop(s)
print("##############清空栈##########")
clear(s)
print("##############遍历元素##########")
getAll(s)

栈的应用

• 函数调用
• 浏览器的前进或者后退
• 表达式求值
• 内存分配

线性结构的两种应用方式之队列

队列的定义

一种可以实现"先进先出"的数据结构

队列的分类

• 链式队列
• 静态队列

链式队列的算法

class Node:
    def __init__(self, value):
        self.data = value
        self.next = None
class Queue:
    def __init__(self):
        self.front = Node(None)
        self.rear = self.front
    def enQueue(self, element):
        n = Node(element)
        self.rear.next = n
        self.rear = n
    def deQueue(self):
        if self.empty():
            print('队空')
            return
        temp = self.front.next
        self.front = self.front.next
        if self.rear == temp:
            self.rear = self.front
        del temp
    def getHead(self):
        if self.empty():
            print('队空')
            return
        return self.front.next.data
    def empty(self):
        return self.rear == self.front
    def printQueue(self):
        cur = self.front.next
        while cur != None:
            print(cur.data)
            cur = cur.next
    def length(self):
        cur = self.front.next
        count = 0
        while cur != None:
            count += 1
            cur = cur.next
        return count
if __name__ == '__main__':
    queue = Queue()
    queue.enQueue(23)
    queue.enQueue(2)
    queue.enQueue(4)
    queue.printQueue()
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)
    queue.deQueue()
    # queue.printQueue()
    l = queue.length()
    print("长度是: %d" % l)

递归

定义

一个函数自己或者间接调用自己

多个函数调用

​ 当有多个函数调用时，按照“先调用后返回”的原则，函数之间的信息传递和控制转移必须借助栈来实现，即系统将整个程序运行时所需要的数据空间安排在一个栈中，每当调用一个函数时，就在栈顶分配一个存储区，进行压栈操作，每当一个函数退出时，就释放他的存储区，即进行出栈操作，当前运行的函数永远在栈顶的位置

def f():
    print('FFFFFFF')
    g()
    
def g():
    print('GGGGGGG')
    k()
    
def k():
    print('KKKKKKK')
    
if __name__ == "__main__":
    f()

自己调用自己也是和上面的原理一样

def f(n):
    if n == 1:
        print('hello')
    else:
        f(n-1)

递归满足的条件

• 递归必须有一个明确的终止条件
• 该函数所处理的数据规模是必须递减的
• 这个转化必须是可解的

求阶乘

n规模的实现，得益于n-1规模的实现

	
# for循环实现
multi = 1
for i in range(3):
    multi = multi * (i+1)
print(multi)
# 递归实现
def f(n):
    if 1 == n:
        return 1
    else:
        return f(n-1)*n

1+2+3+4…+100的和

def sum(n):
    if 1 == n:
        return n
    else:
        return sum(n-1) + n

递归和循环的区别

• 递归
  • 不易于理解
  • 速度慢
  • 存储空间大
• 循环
  • 易于理解
  • 速度快
  • 存储空间小

递归的应用

树和森林就是以递归的方式定义的
树和图的算范就是以递归的方式实现的
很多数学公式就是以递归的方式实现的（斐波那楔序列）

阶段总结

数据结构：
从狭义的方面讲：

• 数据结构就是为了研究数据的存储问题
• 数据结构的存储包含两个方面：个体的存储 + 个体关系的存储

从广义方面来讲：

• 数据结构既包含对数据的存储，也包含对数据的操作
• 对存储数据的操作就是算法

算法
从狭义的方面讲：

• 算法是和数据的存储方式有关的

从广义的方面讲：

• 算法是和数据的存储方式无关，这就是泛型的思想

非线性结构

树

树的定义

我们可以简单的认为：

• 树有且仅有一个根节点
• 有若干个互不相交的子树，这些子树本身也是一颗树

通俗的定义：
1.树就是由节点和边组成的
2.每一个节点只能有一个父节点，但可以有多个子节点。但有一个节点例外，该节点没有父节点，此节点就称为根节点

树的专业术语

• 节点
• 父节点
• 子节点
• 子孙
• 堂兄弟
• 兄弟
• 深度
  • 从根节点到最底层节点的层数被称为深度，根节点是第一层
• 叶子节点
  • 没有子节点的节点
• 度
  • 子节点的个数

树的分类

• 一般树
  • 任意一个节点的子节点的个数不受限制
• 二叉树
  • 定义：任意一个节点的子节点的个数最多是两个，且子节点的位置不可更改
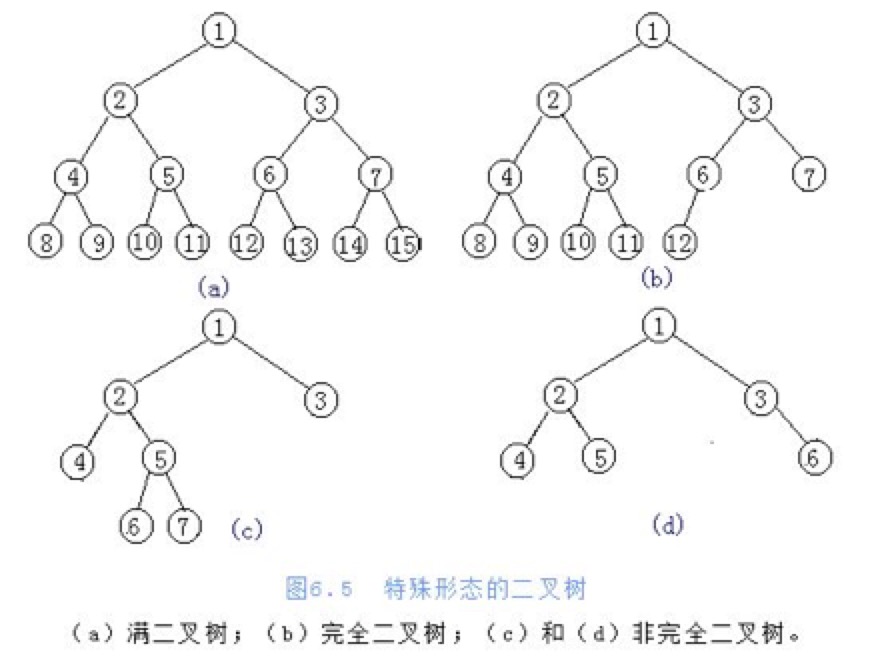
    • 满二叉树
      • 定义：在不增加层数的前提下，无法再多添加一个节点的二叉树
    • 完全二叉树
      • 定义：只是删除了满二叉树最底层最右边连续的若干个节点
    • 一般二叉树
• 森林
  • n个互不相交的数的集合

树的操作(伪算法)

如何把一个非线性结构的数据转换成一个线性结构的数据存储起来？

• 一般树的存储

  • 双亲表示法
    • 求父节点方便
  • 孩子表示法
    • 求子节点方便
  • 双亲孩子表示法
    • 求父节点和子节点都很方便
  • 二叉树表示法
    • 即把一般树转换成二叉树，按照二叉树的方式进行存储
    • 具体的转化办法：
      • 设法保证任意一个节点的：
        • 左指针域指向它的第一个孩子
        • 右指针域指向它的下一个兄弟
      • 只要能满足上述的条件就能够转化成功

• 二叉树的操作

  • 连续存储 （完全二叉树，数组方式进行存储）
    • 优点：查找某个节点的父节点和子节点非常的快
    • 缺点：耗用内存空间过大
    • 转化的方法：先序 中序 后序
  • 链式存储 （链表存储）
    • data区域 左孩子区域 右孩子区域

• 森林的操作

  • 把所有的树转化成二叉树，方法同一般树的转化

二叉树具体的操作

1.二叉树的先序遍历[先访问根节点]

• 先访问根节点
• 再先序遍历左子树
• 再先序遍历右子树

2.二叉树的中序遍历 [中间访问根节点]

• 先中序遍历左子树
• 再访问根节点
• 再中序遍历右子树

3.二叉树的后序遍历 [最后访问根节点]

• 先中序遍历左子树
• 再中序遍历右子树
• 再访问根节点

4.已知先序和中序，如何求出后序？

#### 例一
先序：ABCDEFGH
中序：BDCEAFHG
求后序？
后序：DECBHGFA
#### 例二
先序：ABDGHCEFI
中序：GDHBAECIF
求后序？
后序：GHDBEIFCA

5.已知中序和后序，如何求出先序？

中序：BDCEAFHG
后序：DECBHGFA
求先序？
先序：ABCDEFGH

class Node(object):
    """节点类"""
    def __init__(self, elem=-1, lchild=None, rchild=None):
        self.elem = elem
        self.lchild = lchild
        self.rchild = rchild
class Tree(object):
    """树类"""
    def __init__(self):
        self.root = Node()
        self.myli = []
    def add(self, elem):
        """为树添加节点"""
        node = Node(elem)
        if self.root.elem == -1:  # 如果树是空的，则对根节点赋值
            self.root = node
            self.myli.append(self.root)
        else:
            treeNode = self.myli[0]  # 此结点的子树还没有齐。
            if treeNode.lchild == None:
                treeNode.lchild = node
                self.myli.append(treeNode.lchild)
            else:
                treeNode.rchild = node
                self.myli.append(treeNode.rchild)
                self.myli.pop(0)
    def front_digui(self, root):
        """利用递归实现树的先序遍历"""
        if root == None:
            return
        print(root.elem)
        self.front_digui(root.lchild)
        self.front_digui(root.rchild)
    def middle_digui(self, root):
        """利用递归实现树的中序遍历"""
        if root == None:
            return
        self.middle_digui(root.lchild)
        print(root.elem)
        self.middle_digui(root.rchild)
    def later_digui(self, root):
        """利用递归实现树的后序遍历"""
        if root == None:
            return
        self.later_digui(root.lchild)
        self.later_digui(root.rchild)
        print(root.elem)
   
if __name__ == '__main__':
    """主函数"""
    elems = range(10)           #生成十个数据作为树节点
    tree = Tree()               #新建一个树对象
    for elem in elems:
        tree.add(elem)           #逐个添加树的节点
    print('递归实现先序遍历:')
    tree.front_digui(tree.root)

树的应用

• 树是数据库中数据组织的一种重要形式
• 操作系统子父进程的关系本身就是一颗树
• 面型对象语言中类的继承关系

总结

数据结构研究的就是数据的存储和数据的操作的一门学问

数据的存储又分为两个部分：

• 个体的存储
• 个体关系的存储

从某个角度而言，数据存储最核心的就是个体关系如何进行存储
个体的存储可以忽略不计

推荐学习书籍