这一篇是个人的集训题目心得,看到与洛谷上此题有较大关联,所以放上来了。
题面:

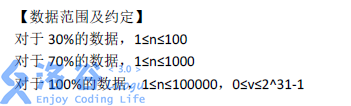
解析:
例图
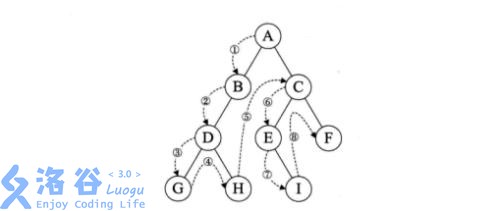
首先我们要知道,要求出任意两点之间的路径异或和,
e.g.1:G——E:
可以得出G——E的路径异或和等于G——A的异或和异或上E——A的路径异或和。
证明:A——G的路径异或和:ABBDDG;
A——E的路径异或和:AC^CE;
把两个异或起来就是ABBDDGACCE;
e.g.2:G——H(换两个有重复的试试?
可以得出G——H的路径异或和等于G——A的异或和异或上H——A的路径异或和。
证明:A——G的路径异或和:ABBDDG;
A——H的路径异或和:ABBDDH;
把两个异或起来:DG^DH
???
为什么两个相同的异或可以抵消呢?
这其实就相当于求ABB=?
我们知道,异或就是按位不进位加法:
1^1=0;
1^0=1;
0^1=1;
0^0=0;
因为是二进制,所以说连续进行两次不进位加法就又返回了原值。
然后就可以得到70%的分数。
要得到100%的分数,我们就要使用一种叫01字典树的做法.
就是把每一个数都转换为二进制,然后转换为一颗字典树,从高位到低位贪心出最大异或和即可。
字典树?
如图:

PS:左下角被挡住的两个单词是inn和int
这是inn, int, at, age, adv, ant这六个单词组成的字典树,我们可以看到,他们每一个单词都有共同开头几个字母。
所以运用一棵字典树,就可以巧妙的按照从跟到其他任意一个节点的方案走出每一个单词。
到了数字里:
因为前文已经说明,要求出任何两个点之间的异或和都可以转换成两者与根之间的关系。
所以,也就可以构造成一颗:01字典树。
其变化就是把字母替换成了0或1,因为单词是又一些字母组成,而一个10进制的数是由一些0和1组成一样。
所以说这样转换后,就可以求贪心求最长异或和了。
比如从根开始找,一直找1就行。
此题与洛谷P4551 最长异或路径很像,但以下代码并不能AC.
代码
#include <stdio.h>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#define maxn 100010
using namespace std;
struct edge{
int next,to,val;
}e[maxn*2];
int point[maxn],cnt,n,xorval[maxn];
int t[maxn*32][2],root,size,ans;
bool vis[maxn];
void addedge(int x,int y,int val)
{
e[++cnt].next=point[x];
e[cnt].to=y;
e[cnt].val=val;
point[x]=cnt;
}
void dfs(int x)
{
vis[x]=1;
for(int i=point[x];i;i=e[i].next)
{
int y=e[i].to;
if(!vis[y])
{
xorval[y]=xorval[x]^e[i].val;
dfs(y);
}
}
}
void insert(int val)
{
int x=root;
for(int i=30;i>=0;i--)
{
int tmp=(val>>i)&1;
if(t[x][tmp]==-1) t[x][tmp]=++size;
x=t[x][tmp];
}
}
void init()
{
memset(t,-1,sizeof(t));
memset(e,0,sizeof(e));
memset(point,0,sizeof(point));
memset(vis,0,sizeof(vis));
memset(xorval,0,sizeof(xorval));
ans=cnt=size=root=0;
}
void query(int val)
{
int x=root;
int sum=0;
for(int i=30;i>=0;i--)
{
int tmp=(val>>i)&1;
if(t[x][tmp^1]==-1)
x=t[x][tmp];
else
{
x=t[x][tmp^1];
sum+=(1<<i);
}
}
ans=max(ans,sum);
}
int main()
{
//freopen("xortree.in","r",stdin);
//freopen("xortree.out","w",stdout);
while(scanf("%d",&n)!=EOF)
{
init();
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
x++;
y++;
addedge(x, y, z);
addedge(y, x, z);
}
dfs(0);//深搜
for(int i=0;i<n;i++)
insert(xorval[i]);
for(int i=0;i<n;i++)
query(xorval[i]);
printf("%d
",ans);
}
}