1. (prufer)序列的定义
(prufer)序列是无根树对应的一种序列,重点是一棵无根树对应一个唯一的prufer序列(不要问我怎么证)
把无根树转换为(prufer)序列的步骤:
- 将编号最小的叶子节点(度数为(1))删除
- 将与这个节点相连的节点加入序列中
- 重复执行(1,2),直到这棵树只剩下两个节点
2. (prufer)序列的实现
我们来求一下(prefer)序列
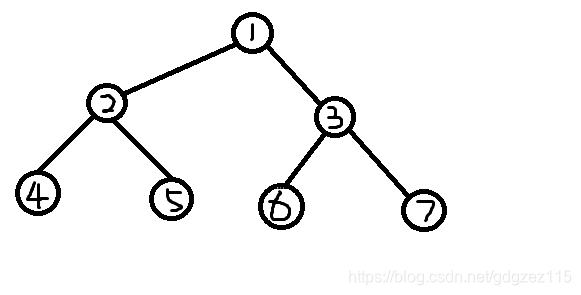
我们看一下上面这幅图
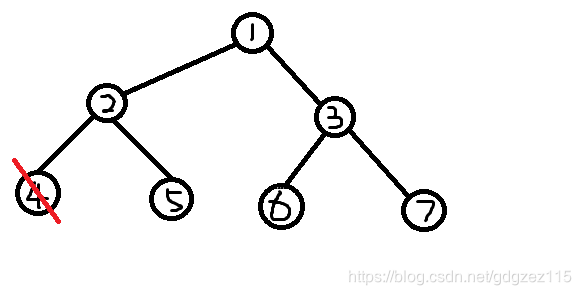
首先,我们删除编号最小的叶子节点(4),并将节点(2)加入序列中
(prufer)序列:(2)
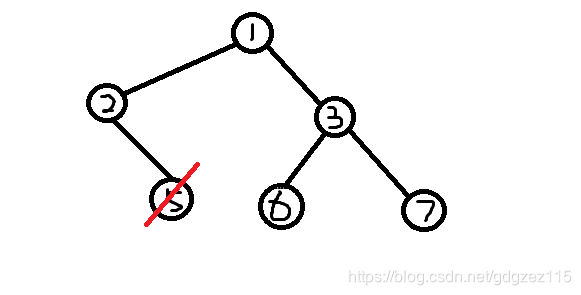
我们删除编号最小的叶子节点(5),将节点(2)加入序列
(prufer)序列:(2,2)
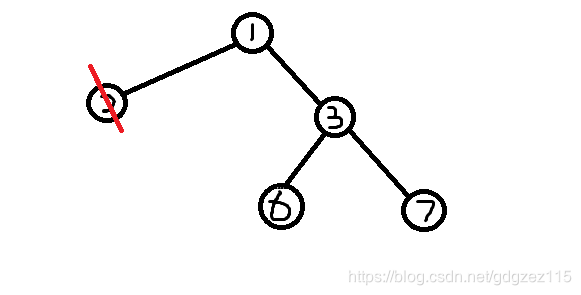
我们删除编号最小的叶子节点(2),将节点(1)加入序列
(prufer)序列:(2,2,1)
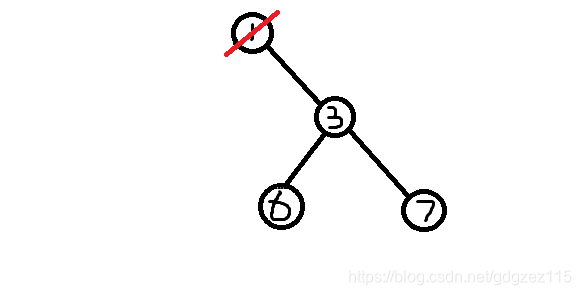
我们删除编号最小的叶子节点(1)(没有根),将节点(3)加入序列
(prufer)序列:(2,2,1,3)
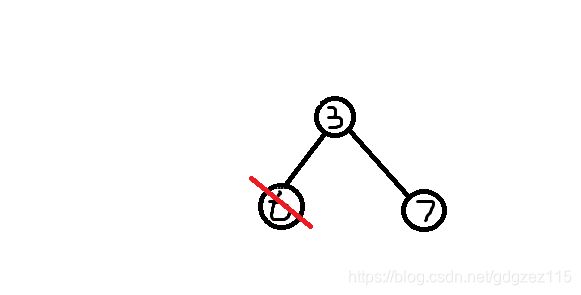
我们删除编号最小的叶子节点(6),将节点(3)加入序列
(prufer)序列:(2,2,1,3,3)
最后只剩下节点(3,7),这样就完成了(prufer)序列的实现
3. (prufer)序列的性质
- (prufer)序列中某个编号出现的个数为它的度数(-1)
- 一棵节点个数为(n)无根树的(prufer)序列长度一定是(n-2)