洛谷——P2296 寻找道路

https://www.luogu.org/problem/show?pid=2296#sub

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2  
1 2  
2 1  
1 3  

输出样例#1：

-1

输入样例#2：

6 6  
1 2  
1 3  
2 6  
2 5  
4 5  
3 4  
1 5  

输出样例#2：

3

说明

解释1：

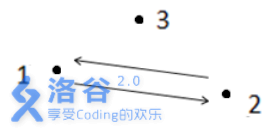
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

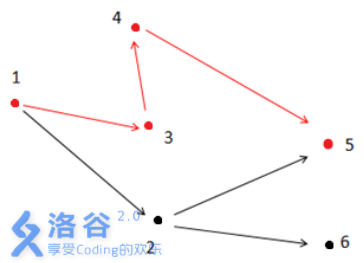
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

Step1 反向BFS求出满足1的得点

Step2 SPFA求出最短路（-1处，加小优化）

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <queue>

using namespace std;

const int N(200005);
int n,m,u,v,s,t;
int sumedge1,head1[N],sumedge2,head2[N];
struct Edge
{
    int from,to,next;
    Edge(int from=0,int to=0,int next=0) :
        from(from),to(to),next(next) {}
}edge1[N*10],edge2[N*10];

void ins1(int from,int to)
{
    edge1[++sumedge1]=Edge(from,to,head1[from]);
    head1[from]=sumedge1;
}
void ins2(int from,int to)
{
    edge2[++sumedge2]=Edge(from,to,head2[from]);
    head2[from]=sumedge2;
}

queue<int>q;
int inq[N],point[N];

void Getpoint()
{
    q.push(t);
    inq[t]=true;
    while(!q.empty())
    {
        int cur=q.front();
        q.pop();
        for(int i=head2[cur];i;i=edge2[i].next)
        {
            v=edge2[i].to;
            if(!inq[v])q.push(v); inq[v]=1;
        }
    }
    for(int i=1;i<=n;i++)
    {
        bool ok=1;
        for(int j=head1[i];j;j=edge1[j].next)
            if(!inq[edge1[j].to])
            {
                ok=0;
                break;
            }
        if(ok) point[i]=1;
    }
}

queue<int>que;
int inque[N],dis[N];

void Spfa()
{
    memset(dis,-1,sizeof(dis));
    dis[s]=0;
    que.push(s); inque[s]=1;
    while(!que.empty())
    {
        int cur=que.front();
        que.pop(); inque[cur]=0;
        for(int i=head1[cur];i;i=edge1[i].next)
        {
            v=edge1[i].to;
            if(point[v]&&dis[v]==-1)
            {
                dis[v]=dis[cur]+1;
                que.push(v); inque[v]=1;
            }
        }
    }
    printf("%d",dis[t]);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(;m;m--)
    {
        scanf("%d%d",&u,&v);
        ins1(u,v); ins2(v,u);
    }
    scanf("%d%d",&s,&t);
    Getpoint(); Spfa();
    return 0;
}