Bzoj2820 YY的GCD

Time Limit: 10 Sec Memory Limit: 512 MB
Submit: 1810 Solved: 967

Description

神犇YY虐完数论后给傻×kAc出了一题给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对kAc这种

傻×必然不会了，于是向你来请教……多组输入

Input

第一行一个整数T 表述数据组数接下来T行，每行两个正整数，表示N, M

Output

T行，每行一个整数表示第i组数据的结果

Sample Input

2
10 10
100 100

Sample Output

30
2791

HINT

T = 10000

N, M <= 10000000

Source

数学问题莫比乌斯反演脑洞大开题

此题非常神！

iwtwiioi的题解http://www.cnblogs.com/iwtwiioi/p/4132095.html

Bzoj1101这里探究了对于给定的d，如何求一定范围内gcd(i,j)==d的数对的数量 http://www.cnblogs.com/SilverNebula/p/6582843.html

在这里多了gcd是质数的限制。

OKわかった，只要枚举范围内的每个质数，分别求数对数量并累加就可以了

↓像这样

 1 /*by SilverN*/
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<cstring>
 5 #include<cstdio>
 6 #include<cmath>
 7 #include<vector>
 8 #define LL long long
 9 using namespace std;
10 const int mxn=10000005;
11 int read(){
12     int x=0,f=1;char ch=getchar();
13     while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
14     while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
15     return x*f;
16 }
17 int pri[mxn],mu[mxn],cnt=0;
18 int smm[mxn];
19 bool vis[mxn];
20 void init(){
21     mu[1]=1;
22     for(int i=2;i<mxn;i++){
23         if(!vis[i]){
24             pri[++cnt]=i;
25             mu[i]=-1;
26         }
27         for(int j=1;j<=cnt && (LL)pri[j]*i<mxn;j++){
28             vis[pri[j]*i]=1;
29             if(i%pri[j]==0){mu[pri[j]*i]=0;break;}
30             mu[pri[j]*i]=-mu[i];
31         }
32     }
33     for(register int i=1;i<mxn;i++)
34         smm[i]=smm[i-1]+mu[i];
35     return;
36 }
37 LL calc(int a,int b){
38     LL res=0;int pos;
39     if(a>b)swap(a,b);
40     for(int i=1;i<=a;i=pos+1){
41         int x=a/i,y=b/i;
42         pos=min(a/x,b/y);
43         res+=(smm[pos]-smm[i-1])*x*y;
44     }
45     return res;
46 }
47 LL solve(int n,int m){
48     if(n>m)swap(n,m);
49     LL res=0;int pos;
50     for(int i=1;i<=cnt;i++){//枚举范围内的每个质数 
51         if(pri[i]>n)break;
52         res+=calc(n/pri[i],m/pri[i]);
53     }
54     return res;
55 }
56 int T;
57 int n,m;
58 int main(){
59     int i,j;
60     init();
61     T=read();
62     while(T--){
63         n=read();m=read();
64         LL ans=solve(n,m);
65         printf("%lld
",ans);
66     }
67     return 0;
68 }

TLE

↑

然而代码标题那三个字母说明事情并没有那么简单……

我们需要更快的算法。如果外部枚举prime的过程也能像内部一样分块求，那么复杂度又能大大降低。

于是脑洞大开搞出了这样的公式：

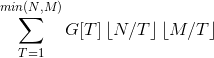具体过程见上方链接

(T=prime*d)

现在只要仿照莫比乌斯函那样搞出来一个“自动化”的容斥函数G[T]就可以了

 1 /*by SilverN*/
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<cstring>
 5 #include<cstdio>
 6 #include<cmath>
 7 #include<vector>
 8 #define LL long long
 9 using namespace std;
10 const int mxn=10000005;
11 int read(){
12     int x=0,f=1;char ch=getchar();
13     while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
14     while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
15     return x*f;
16 }
17 int pri[mxn],mu[mxn],cnt=0;
18 int g[mxn];
19 int smm[mxn];
20 bool vis[mxn];
21 void init(){
22     mu[1]=1;g[1]=0;
23     for(int i=2;i<mxn;i++){
24         if(!vis[i]){
25             pri[++cnt]=i;
26             mu[i]=-1;g[i]=1;
27         }
28         for(int j=1;j<=cnt && (LL)pri[j]*i<mxn;j++){
29             vis[pri[j]*i]=1;
30             if(i%pri[j]==0){mu[pri[j]*i]=0;g[pri[j]*i]=mu[i]; break;}
31             mu[pri[j]*i]=-mu[i];
32             g[pri[j]*i]=mu[i]-g[i];
33         }
34     }
35     for(register int i=1;i<mxn;i++)
36         smm[i]=smm[i-1]+g[i];
37     return;
38 }
39 LL calc(int a,int b){
40     LL res=0;int pos;
41     if(a>b)swap(a,b);
42     for(int i=1;i<=a;i=pos+1){
43         int x=a/i,y=b/i;
44         pos=min(a/x,b/y);
45         res+=(LL)(smm[pos]-smm[i-1])*x*y;
46     }
47     return res;
48 }
49 int T;
50 int n,m;
51 int main(){
52     int i,j;
53     init();
54     T=read();
55     while(T--){
56         n=read();m=read();
57         LL ans=calc(n,m);
58         printf("%lld
",ans);
59     }
60     return 0;
61 }