Submit: 3823 Solved: 1115
Description
某公司加工一种由铁、铝、锡组成的合金。他们的工作很简单。首先进口一些铁铝锡合金原材料,不同种类的
原材料中铁铝锡的比重不同。然后,将每种原材料取出一定量,经过融解、混合,得到新的合金。新的合金的铁铝
锡比重为用户所需要的比重。 现在,用户给出了n种他们需要的合金,以及每种合金中铁铝锡的比重。公司希望能
够订购最少种类的原材料,并且使用这些原材料可以加工出用户需要的所有种类的合金。
Input
第一行两个整数m和n(m, n ≤ 500),分别表示原材料种数和用户需要的合金种数。第2到m + 1行,每行三
个实数a, b, c(a, b, c ≥ 0 且 a + b + c = 1),分别表示铁铝锡在一种原材料中所占的比重。第m + 2到m +
n + 1行,每行三个实数a, b, c(a, b, c ≥ 0 且 a + b + c = 1),分别表示铁铝锡在一种用户需要的合金中
所占的比重。
Output
一个整数,表示最少需要的原材料种数。若无解,则输出–1。
Sample Input
0.1 0.2 0.7
0.2 0.3 0.5
0.3 0.4 0.3
0.4 0.5 0.1
0.5 0.1 0.4
0.6 0.2 0.2
0.7 0.3 0
0.8 0.1 0.1
0.9 0.1 0
1 0 0
0.1 0.2 0.7
0.2 0.3 0.5
0.3 0.4 0.3
0.4 0.5 0.1
0.5 0.1 0.4
0.6 0.2 0.2
0.7 0.3 0
0.8 0.1 0.1
0.9 0.1 0
1 0 0
Sample Output
HINT
Source
数学 计算几何 凸包思想 floyd
由于a+b+c=1,第三维可以用前两维表示,所以可以不考虑。
↓以下说明中n和m意义和题目中相反(傻傻看反了)
二维情况下,几个点围成的区域就是它们可以表示出的区域。
枚举n中任意两点,若所有m点都在这两点所连有向线段的左边,则可以选这条线段。将线段看作“边”,在邻接矩阵上标记出各点到另外点的转移关系,floyd求最小环即可。
然后特判所有点共点的情况。
——————
脑洞出一种奇怪的方法:
枚举凸包上某个点作为起点,遍历后面的凸包上点,如果m个点都在p[i] to p[i-2] 这条线段的左边,那么p[i],p[i-1],p[i-2]围成的三角形就没用了,可以把p[i-1]舍弃掉
枚举起点O(n),遍历凸包O(n),判是否可行O(m),总时间复杂度O(n*n*m)
拍了半天没问题的样子,但是交上去过不了,目测是在判断能否围成环的时候出了bug,要么就是少了什么特判
还是先放着吧

1 /*by SilverN*/
2 #include<algorithm>
3 #include<iostream>
4 #include<cstring>
5 #include<cstdio>
6 #include<cmath>
7 #include<vector>
8 using namespace std;
9 const double eps=1e-8;
10 const int mxn=100010;
11 struct Point{
12 double x,y;
13 Point operator + (Point b){ return (Point){x+b.x,y+b.y};}
14 Point operator - (Point b){ return (Point){x-b.x,y-b.y};}
15 double operator * (Point b){return x*b.x+y*b.y;}
16 bool operator < (Point b)const{
17 return x<b.x || (x==b.x && y<b.y);
18 }
19 }p[mxn],a[mxn],bas[mxn];
20 typedef Point Vector;
21 double Cross(Point a,Point b){return a.x*b.y-a.y*b.x;}
22 int n,m;
23 int ans;
24 bool judge(Point x,Point y){
25 for(int i=1;i<=m;i++){
26 double cro=Cross(y-x,a[i]-x);
27 if(cro<-eps)return 0;
28 if(fabs(cro)<eps && (x-a[i])*(y-a[i])>eps){
29 return 0;
30 }
31 }
32 return 1;
33 }
34
35 int st[mxn],top,t2;
36 void Andrew(){
37 sort(p+1,p+n+1);
38 for(int i=1;i<=n;i++){
39 while(top>1 && Cross(p[st[top]]-p[st[top-1]],p[i]-p[st[top]])<0)top--;
40 st[++top]=i;
41 }
42 t2=top;
43 for(int i=n-1;i;i--){
44 while(t2>top && Cross(p[st[t2]]-p[st[t2-1]],p[i]-p[st[t2]])<0)t2--;
45 st[++t2]=i;
46 }
47 for(int i=1;i<=t2;i++){
48 printf("%.3f %.3f
",p[st[i]].x,p[st[i]].y);
49 }
50 printf("fin
");*/
51 memcpy(bas,p,sizeof p);
52 for(int i=1;i<=t2;i++)p[i]=bas[st[i]];
53 n=t2-1;
54 return;
55 }
56 void solve(int ST){
57 // printf("st:%d
",ST);
58 st[top=1]=ST;
59 for(int i=1,tmp=ST+1;i<n;i++,tmp++){
60 if(tmp>n)tmp-=n;
61 if(top>1 && fabs(Cross(p[tmp]-p[st[top]],p[(tmp%n)+1]-p[tmp]))<eps)continue;
62 // printf("tmp:%d pt:%.3f %.3f
",tmp,p[tmp].x,p[tmp].y);
63 bool flag=judge(p[st[top-1]],p[tmp]);
64 // printf("last:%.3f %.3f now:%.3f %.3f
",p[st[top-1]].x,p[st[top-1]].y,p[tmp].x,p[tmp].y);
65 // printf("flag:%d
",flag);
66 if(top>1 && flag){
67 st[top]=tmp;
68 }
69 else if(judge(p[st[top]],p[tmp]))st[++top]=tmp;
70 else return;
71 }
72 if(top==2 && judge(p[st[top-1]],p[st[top]])){
73 ans=min(ans,2);return;
74 }
75 if(st[top]==ST)top--;
76 if(!judge(p[st[top]],p[ST]))return;
77 ans=min(ans,top);
78 return;
79 }
80 bool SPJ(){
81 for(int i=1;i<=n;i++)
82 if(fabs(p[i].x-p[1].x)>eps || fabs(p[i].y-p[1].y)>eps)return 0;
83 for(int i=1;i<=m;i++)
84 if(fabs(a[i].x-p[1].x)>eps || fabs(a[i].y-p[1].y)>eps)return 0;
85 return 1;
86 }
87 int main(){
88 // freopen("Input.in","r",stdin);
89 int i,j;
90 scanf("%d%d",&n,&m);
91 for(i=1;i<=n;i++){
92 scanf("%lf%lf%*lf",&p[i].x,&p[i].y);
93 }
94 for(i=1;i<=m;i++){
95 scanf("%lf%lf%*lf",&a[i].x,&a[i].y);
96 }
97 if(!m){
98 printf("0
");return 0;
99 }
100 if(SPJ()){
101 printf("1
");return 0;
102 }
103 Andrew();
104 ans=0x3f3f3f3f;
105 for(i=1;i<=n;i++){
106 solve(i);
107 }
108 if(ans==0x3f3f3f3f || !ans)ans=-1;
109 printf("%d
",ans);
110 return 0;
111 }
————updated 4.5
果然还是放不下这个坑,正巧幸运地找到了测试数据,发现只WA了一个点,于是又想了好久,找到了几种hack。
这种写法最大的问题在于:必须先处理出凸包,再在凸包上删点,如果正确答案在4个点及以上,在凸包上算的正确性显然,否则会有一些问题:
比如:
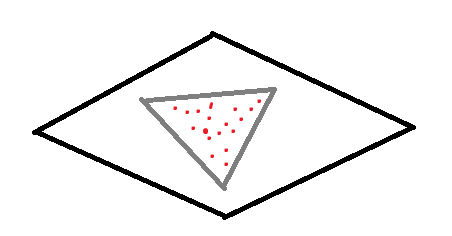
↑最小环并不是由凸包上点围成的,答案为3

两点确定的直线可以包括所有合金,并不需要圈起来,答案为2
以及所有m都挤在同一点,答案为1
于是挨个加入特判,修改代码细节,代码变得又(sang)臭(xin)又(bing)长(kuang)
复杂度:
首先需要一个$O(n*m)$的“聚在一点”判断(如果先枚举m,发现m聚在一点再查找n可以优化到$O(m+n)$,改不动了)。
如果答案不为1,还需要一个$O(m*n^2)$的共线特判;
如果答案不为2,进行$O(n*n*m)$的凸包上计算,如果跑出来答案是4,加一个$O(m*n^3)$的特判;
然后A掉了,120ms,似乎比大部分floyd跑得快,比精巧的floyd跑得慢
用floyd的话,时间复杂度是稳定$O(n^3)$ ……我选择死亡
实在不知道status里面那些20+ms的怎么做到的……
目前还想到一个优化:取消在凸包上枚举起点,而是任选一个起点,开始沿着凸包转转转转,如果转了一圈都没能再更新答案,就退出。
(但是正确性未知)
这样在随机数据下大概能优化掉一个n,时间复杂度变为$O(n*m)$
期望复杂度是……我怎么可能会算啊(掀桌)
↑感觉有点类似旋转卡壳了(并不)
↑但是实现起来超麻烦的样子(博主比较蠢)
↑于是放弃了
MD大概不会有人和我一样无聊到写这种诡异解法了,就算有也肯定写得短小精悍效率高

1 /*by SilverN*/ 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 using namespace std; 9 const double eps=1e-7; 10 const int mxn=100010; 11 struct Point{ 12 double x,y; 13 Point operator + (Point b){ return (Point){x+b.x,y+b.y};} 14 Point operator - (Point b){ return (Point){x-b.x,y-b.y};} 15 double operator * (Point b){return x*b.x+y*b.y;} 16 bool operator < (Point b)const{ 17 return x<b.x || (x==b.x && y<b.y); 18 } 19 }p[mxn],a[mxn],bas[mxn]; 20 typedef Point Vector; 21 double Cross(Point a,Point b){return a.x*b.y-a.y*b.x;} 22 int n,m; 23 int ans; 24 inline int DT(double x){ 25 if(fabs(x)<eps)return 0; 26 return x<0?-1:1; 27 } 28 bool judge(Point x,Point y){ 29 for(int i=1;i<=m;i++){ 30 double cro=Cross(y-x,a[i]-x); 31 if(cro<-eps)return 0; 32 if(fabs(cro)<eps && DT((x-a[i])*(y-a[i]))>eps){ 33 return 0; 34 } 35 } 36 return 1; 37 } 38 int st[mxn],top,t2; 39 void Andrew(){ 40 sort(p+1,p+n+1); 41 for(int i=1;i<=n;i++){ 42 while(top>1 && DT(Cross(p[st[top]]-p[st[top-1]],p[i]-p[st[top-1]]))<0)top--; 43 st[++top]=i; 44 } 45 t2=top; 46 for(int i=n-1;i;i--){ 47 while(t2>top && DT(Cross(p[st[t2]]-p[st[t2-1]],p[i]-p[st[t2-1]]))<0)t2--; 48 st[++t2]=i; 49 } 50 memcpy(bas,p,sizeof p); 51 for(int i=1;i<=t2;i++)p[i]=bas[st[i]]; 52 // n=t2; 53 n=t2-1; 54 return; 55 } 56 void solve(int ST){ 57 if(m==1){ 58 if(abs(p[ST].x-a[1].x)<eps && abs(p[ST].y-a[1].y)<eps){ 59 ans=1; 60 return; 61 } 62 } 63 st[top=1]=ST; 64 for(int i=1,tmp=ST+1;i<=n;i++,tmp++){ 65 if(tmp>n)tmp-=n; 66 if(top==1){ 67 st[++top]=tmp; 68 continue; 69 } 70 if(top>1 && fabs(Cross(p[tmp]-p[st[top]],p[(tmp%n)+1]-p[tmp]))<=eps)continue; 71 bool flag=judge(p[st[top-1]],p[tmp]); 72 if(top>1 && flag){ 73 st[top]=tmp; 74 } 75 else if(judge(p[st[top]],p[tmp]))st[++top]=tmp; 76 else return; 77 if(top>ans)return;//剪枝 78 } 79 if(top==1)return; 80 if(top==2){ 81 if(!judge(p[st[top-1]],p[st[top]]) || !judge(p[st[top]],p[st[top-1]]))return; 82 ans=min(ans,2);return; 83 } 84 if(st[top]==ST)top--; 85 if(!judge(p[st[top]],p[ST]))return; 86 int res=top; 87 ans=min(ans,res); 88 return; 89 } 90 bool SPJ(){//共点特判1 91 for(int i=1;i<=n;i++) 92 if(fabs(p[i].x-p[1].x)>eps || fabs(p[i].y-p[1].y)>eps)return 0; 93 for(int i=1;i<=m;i++) 94 if(fabs(a[i].x-p[1].x)>eps || fabs(a[i].y-p[1].y)>eps)return 0; 95 return 1; 96 } 97 bool SPJ_Point(){//共点特判2 98 int i,j; 99 for(i=1;i<=n;i++){ 100 for(j=1;j<=m;j++){ 101 if(abs(p[i].x-a[j].x)>eps || abs(p[i].y-a[j].y)>eps)break; 102 } 103 if(j==m+1){ 104 printf("1 "); 105 exit(0); 106 } 107 } 108 return 0; 109 } 110 bool SPJ_Line(){//直线特判 111 int i,j; 112 for(i=1;i<=n;i++){ 113 for(j=1;j<=n;j++){ 114 if(i==j)continue; 115 if(judge(p[i],p[j]) && judge(p[j],p[i])){ 116 printf("2 "); 117 exit(0); 118 } 119 } 120 } 121 return 0; 122 } 123 void SPJ_tir(){//非凸包上三点的特判 124 for(int i=1;i<=n;i++){ 125 for(int j=1;j<=n;j++){ 126 if(i==j)continue; 127 for(int k=1;k<=n;k++){ 128 if(k==j || k==i)continue; 129 if(judge(bas[i],bas[j]) && judge(bas[j],bas[k]) && judge(bas[k],bas[i])){ 130 printf("3 "); 131 exit(0); 132 } 133 } 134 } 135 } 136 } 137 int main(){ 138 // freopen("Input.in","r",stdin); 139 // freopen("in.txt","r",stdin); 140 int i,j; 141 scanf("%d%d",&n,&m); 142 for(i=1;i<=n;i++){ 143 scanf("%lf%lf%*lf",&p[i].x,&p[i].y); 144 p[i].x*=1000;p[i].y*=1000; 145 } 146 for(i=1;i<=m;i++){ 147 scanf("%lf%lf%*lf",&a[i].x,&a[i].y); 148 a[i].x*=1000;a[i].y*=1000; 149 } 150 if(!m){ 151 printf("0 ");return 0; 152 } 153 if(SPJ()){ 154 printf("1 ");return 0; 155 } 156 SPJ_Point(); 157 SPJ_Line(); 158 Andrew(); 159 ans=0x3f3f3f3f; 160 for(i=1;i<=n;i++){ 161 solve(i); 162 } 163 if(ans==0x3f3f3f3f || !ans)ans=-1; 164 /* if(ans==4){ 165 SPJ_tir(); 166 }*///发现测试数据里没有用得上这个特判的 167 printf("%d ",ans); 168 return 0; 169 }
感谢数据弱(黄学长和QQQ爷说的)
——————
正解floyd:
1 /*by SilverN*/ 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 using namespace std; 9 const double eps=1e-8; 10 const int INF=0x3f3f3f3f; 11 const int mxn=10010; 12 struct Point{ 13 double x,y; 14 Point operator + (Point b){ return (Point){x+b.x,y+b.y};} 15 Point operator - (Point b){ return (Point){x-b.x,y-b.y};} 16 double operator * (Point b){return x*b.x+y*b.y;} 17 bool operator < (Point b)const{ 18 return x<b.x || (x==b.x && y<b.y); 19 } 20 }p[mxn],a[mxn],bas[mxn]; 21 typedef Point Vector; 22 double Cross(Point a,Point b){return a.x*b.y-a.y*b.x;} 23 int n,m; 24 int ans; 25 bool judge(Point x,Point y){ 26 for(int i=1;i<=m;i++){ 27 double cro=Cross(x-a[i],y-a[i]); 28 if(cro>eps)return 0; 29 if(fabs(cro)<eps && (x-a[i])*(y-a[i])>eps)return 0; 30 } 31 return 1; 32 } 33 bool SPJ(){ 34 for(int i=1;i<=n;i++) 35 if(fabs(p[i].x-p[1].x)>eps || fabs(p[i].y-p[1].y)>eps)return 0; 36 for(int i=1;i<=m;i++) 37 if(fabs(a[i].x-p[1].x)>eps || fabs(a[i].y-p[1].y)>eps)return 0; 38 return 1; 39 } 40 int mp[510][510]; 41 int main(){ 42 // freopen("Input.in","r",stdin); 43 int i,j; 44 scanf("%d%d",&n,&m); 45 for(i=1;i<=n;i++){ 46 scanf("%lf%lf%*lf",&p[i].x,&p[i].y); 47 // p[i].x*=10;p[i].y*=10; 48 } 49 if(!m){ printf("0 ");return 0;} 50 for(i=1;i<=m;i++){ 51 scanf("%lf%lf%*lf",&a[i].x,&a[i].y); 52 // a[i].x*=10;a[i].y*=10; 53 } 54 if(SPJ()){ 55 printf("1 "); 56 return 0; 57 } 58 for(i=1;i<=n;i++){ 59 mp[i][i]=INF; 60 for(j=1;j<=n;j++){ 61 if(i==j)continue; 62 if(judge(p[i],p[j])) mp[i][j]=1; 63 else mp[i][j]=INF; 64 } 65 } 66 for(int k=1;k<=n;k++){ 67 for(i=1;i<=n;i++){ 68 for(j=1;j<=n;j++) 69 mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]); 70 } 71 } 72 ans=INF; 73 for(i=1;i<=n;i++)ans=min(ans,mp[i][i]); 74 if(ans==INF)ans=-1; 75 printf("%d ",ans); 76 return 0; 77 }
