Submit: 309 Solved: 146
Description
Frank对天文学非常感兴趣,他经常用望远镜看星星,同时记录下它们的信息,比如亮度、颜色等等,进而估算出
星星的距离,半径等等。Frank不仅喜欢观测,还喜欢分析观测到的数据。他经常分析两个参数之间(比如亮度和
半径)是否存在某种关系。现在Frank要分析参数X与Y之间的关系。他有n组观测数据,第i组观测数据记录了x_i和
y_i。他需要一下几种操作1 L,R:用直线拟合第L组到底R组观测数据。用xx表示这些观测数据中x的平均数,用yy
表示这些观测数据中y的平均数,即
xx=Σx_i/(R-L+1)(L<=i<=R)
yy=Σy_i/(R-L+1)(L<=i<=R)
如果直线方程是y=ax+b,那么a应当这样计算:
a=(Σ(x_i-xx)(y_i-yy))/(Σ(x_i-xx)(x_i-xx)) (L<=i<=R)
你需要帮助Frank计算a。
2 L,R,S,T:
Frank发现测量数据第L组到底R组数据有误差,对每个i满足L <= i <= R,x_i需要加上S,y_i需要加上T。
3 L,R,S,T:
Frank发现第L组到第R组数据需要修改,对于每个i满足L <= i <= R,x_i需要修改为(S+i),y_i需要修改为(T+i)。
Input
第一行两个数n,m,表示观测数据组数和操作次数。
接下来一行n个数,第i个数是x_i。
接下来一行n个数,第i个数是y_i。
接下来m行,表示操作,格式见题目描述。
1<=n,m<=10^5,0<=|S|,|T|,|x_i|,|y_i|<=10^5
保证1操作不会出现分母为0的情况。
Output
对于每个1操作,输出一行,表示直线斜率a。
选手输出与标准输出的绝对误差不超过10^-5即为正确。
Sample Input
3 5
1 2 3
1 2 3
1 1 3
2 2 3 -3 2
1 1 2
3 1 2 2 1
1 1 3
1 2 3
1 2 3
1 1 3
2 2 3 -3 2
1 1 2
3 1 2 2 1
1 1 3
Sample Output
1.0000000000
-1.5000000000
-0.6153846154
-1.5000000000
-0.6153846154
HINT
Source
树 线段树 数学
把式子展开,发现只有四个变量有关:
$ sum x^2 $ $ sum x*y $ $sum x$ $ sum y $
2操作就是区间加
3操作的结果是一条直线,怎么处理?
像[SDOI2016]游戏 那样用李超线段树维护说不定可以,然而根本用不着那么麻烦。
先将区间覆盖成l~r的x=y的等差数列,然后加一个2操作即可。
等差数列的值用求和公式算:

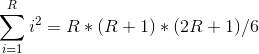
注意区间覆盖的时候要把被覆盖区间的其他tag清空
1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 #define LL long long 9 using namespace std; 10 const int mxn=100010; 11 int read(){ 12 int x=0,f=1;char ch=getchar(); 13 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 14 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 15 return x*f; 16 } 17 struct SGT{ 18 double sx,sy; 19 double xy; double X2; 20 double mkx,mky; 21 int cv; 22 }t[mxn<<2]; 23 #define lc rt<<1 24 #define rc rt<<1|1 25 inline void pushup(int rt){ 26 int Lc=lc,Rc=rc; 27 t[rt].sx=t[Lc].sx+t[Rc].sx; t[rt].sy=t[Lc].sy+t[Rc].sy; 28 t[rt].X2=t[Lc].X2+t[Rc].X2; t[rt].xy=t[Lc].xy+t[Rc].xy; 29 return; 30 } 31 inline LL lsum(LL x,LL y){ 32 return y*(y+1)/2 - x*(x+1)/2; 33 } 34 inline LL sqsum(LL x,LL y){ 35 return y*(y+1)*(2*y+1)/6 - x*(x+1)*(2*x+1)/6; 36 } 37 void addCV(int l,int r,int rt){ 38 LL tmp=sqsum(l-1,r);//l-1 39 t[rt].X2=tmp; t[rt].xy=tmp; 40 t[rt].sx=t[rt].sy=lsum(l-1,r); 41 t[rt].mkx=t[rt].mky=0; 42 // t[rt].cv=1; 43 return; 44 } 45 void addX(LL S,int l,int r,int rt){ 46 t[rt].X2+=2*S*t[rt].sx+S*S*(r-l+1); 47 t[rt].sx+=S*(r-l+1); 48 t[rt].xy+=S*t[rt].sy; 49 // t[rt].mkx+=S; 50 return; 51 } 52 void addY(LL T,int l,int r,int rt){ 53 t[rt].xy+=T*t[rt].sx; 54 t[rt].sy+=T*(r-l+1); 55 // t[rt].mky+=T; 56 return; 57 } 58 void PD(int l,int r,int rt){ 59 int mid=(l+r)>>1; 60 if(t[rt].cv){ 61 addCV(l,mid,lc); addCV(mid+1,r,rc); 62 t[rt].cv=0; 63 t[lc].cv=1;t[rc].cv=1; 64 } 65 if(t[rt].mkx){ 66 addX(t[rt].mkx,l,mid,lc); addX(t[rt].mkx,mid+1,r,rc); 67 t[lc].mkx+=t[rt].mkx; t[rc].mkx+=t[rt].mkx; 68 t[rt].mkx=0; 69 } 70 if(t[rt].mky){ 71 addY(t[rt].mky,l,mid,lc); addY(t[rt].mky,mid+1,r,rc); 72 t[lc].mky+=t[rt].mky; t[rc].mky+=t[rt].mky; 73 t[rt].mky=0; 74 } 75 return; 76 } 77 void update(int L,int R,int S,int T,int l,int r,int rt){ 78 if(L<=l && r<=R){ 79 addX(S,l,r,rt); addY(T,l,r,rt); 80 t[rt].mkx+=S; t[rt].mky+=T; 81 return; 82 } 83 PD(l,r,rt); 84 int mid=(l+r)>>1; 85 if(L<=mid)update(L,R,S,T,l,mid,lc); 86 if(R>mid)update(L,R,S,T,mid+1,r,rc); 87 pushup(rt); 88 return; 89 } 90 void cover(int L,int R,int l,int r,int rt){ 91 if(L<=l && r<=R){ 92 addCV(l,r,rt); 93 t[rt].cv=1; 94 return; 95 } 96 PD(l,r,rt); 97 int mid=(l+r)>>1; 98 if(L<=mid)cover(L,R,l,mid,lc); 99 if(R>mid)cover(L,R,mid+1,r,rc); 100 pushup(rt); 101 return; 102 } 103 int wx[mxn],wy[mxn]; 104 void Build(int l,int r,int rt){ 105 if(l==r){ 106 t[rt].sx=wx[l]; t[rt].sy=wy[l]; 107 t[rt].xy=(LL)wx[l]*wy[l]; 108 t[rt].X2=(LL)wx[l]*wx[l]; 109 return; 110 } 111 int mid=(l+r)>>1; 112 Build(l,mid,lc);Build(mid+1,r,rc); 113 pushup(rt); 114 return; 115 } 116 double Sxy,Sx,Sy,Sxx; 117 void query(int L,int R,int l,int r,int rt){ 118 // printf("que:L:%d R:%d l:%d r:%d rt:%d ",L,R,l,r,rt); 119 if(L<=l && r<=R){ 120 Sxy+=t[rt].xy; 121 Sx+=t[rt].sx;Sy+=t[rt].sy; 122 Sxx+=t[rt].X2; 123 return; 124 } 125 PD(l,r,rt); 126 int mid=(l+r)>>1; 127 if(L<=mid)query(L,R,l,mid,lc); 128 if(R>mid)query(L,R,mid+1,r,rc); 129 pushup(rt); 130 return; 131 } 132 #undef lc 133 #undef rc 134 int n,m; 135 int main(){ 136 // freopen("relative5.in","r",stdin); 137 // freopen("out.txt","w",stdout); 138 int i,j; 139 n=read();m=read(); 140 for(i=1;i<=n;i++)wx[i]=read(); 141 for(i=1;i<=n;i++)wy[i]=read(); 142 Build(1,n,1); 143 int op,L,R,S,T; 144 while(m--){ 145 op=read(); 146 switch(op){ 147 case 1:{ 148 L=read();R=read(); 149 Sxy=Sx=Sy=Sxx=0; 150 query(L,R,1,n,1); 151 double ans=(Sxy-Sx*Sy/(double)(R-L+1))/(double)(Sxx-Sx*Sx/(double)(R-L+1)); 152 printf("%.10f ",ans); 153 break; 154 } 155 case 2:{ 156 L=read();R=read();S=read();T=read(); 157 update(L,R,S,T,1,n,1); 158 break; 159 } 160 case 3:{ 161 L=read();R=read();S=read();T=read(); 162 cover(L,R,1,n,1); 163 update(L,R,S,T,1,n,1); 164 break; 165 } 166 } 167 } 168 return 0; 169 }
Submit: 309 Solved: 146
[Submit][Status][Discuss]
Description
Frank对天文学非常感兴趣,他经常用望远镜看星星,同时记录下它们的信息,比如亮度、颜色等等,进而估算出
星星的距离,半径等等。Frank不仅喜欢观测,还喜欢分析观测到的数据。他经常分析两个参数之间(比如亮度和
半径)是否存在某种关系。现在Frank要分析参数X与Y之间的关系。他有n组观测数据,第i组观测数据记录了x_i和
y_i。他需要一下几种操作1 L,R:用直线拟合第L组到底R组观测数据。用xx表示这些观测数据中x的平均数,用yy
表示这些观测数据中y的平均数,即
xx=Σx_i/(R-L+1)(L<=i<=R)
yy=Σy_i/(R-L+1)(L<=i<=R)
如果直线方程是y=ax+b,那么a应当这样计算:
a=(Σ(x_i-xx)(y_i-yy))/(Σ(x_i-xx)(x_i-xx)) (L<=i<=R)
你需要帮助Frank计算a。
2 L,R,S,T:
Frank发现测量数据第L组到底R组数据有误差,对每个i满足L <= i <= R,x_i需要加上S,y_i需要加上T。
3 L,R,S,T:
Frank发现第L组到第R组数据需要修改,对于每个i满足L <= i <= R,x_i需要修改为(S+i),y_i需要修改为(T+i)。
Input
第一行两个数n,m,表示观测数据组数和操作次数。
接下来一行n个数,第i个数是x_i。
接下来一行n个数,第i个数是y_i。
接下来m行,表示操作,格式见题目描述。
1<=n,m<=10^5,0<=|S|,|T|,|x_i|,|y_i|<=10^5
保证1操作不会出现分母为0的情况。
Output
对于每个1操作,输出一行,表示直线斜率a。
选手输出与标准输出的绝对误差不超过10^-5即为正确。
Sample Input
3 5
1 2 3
1 2 3
1 1 3
2 2 3 -3 2
1 1 2
3 1 2 2 1
1 1 3
1 2 3
1 2 3
1 1 3
2 2 3 -3 2
1 1 2
3 1 2 2 1
1 1 3
Sample Output
1.0000000000
-1.5000000000
-0.6153846154
-1.5000000000
-0.6153846154