Time Limit: 16000/8000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 999 Accepted Submission(s): 434
Problem Description
Perhaps the sea‘s definition of a shell is the pearl. However, in my view, a shell necklace with n beautiful shells contains the most sincere feeling for my best lover Arrietty, but even that is not enough.
Suppose the shell necklace is a sequence of shells (not a chain end to end). Considering i continuous shells in the shell necklace, I know that there exist different schemes to decorate the i shells together with one declaration of love.
I want to decorate all the shells with some declarations of love and decorate each shell just one time. As a problem, I want to know the total number of schemes.
Suppose the shell necklace is a sequence of shells (not a chain end to end). Considering i continuous shells in the shell necklace, I know that there exist different schemes to decorate the i shells together with one declaration of love.
I want to decorate all the shells with some declarations of love and decorate each shell just one time. As a problem, I want to know the total number of schemes.
Input
There are multiple test cases(no more than 20 cases and no more than 1 in extreme case), ended by 0.
For each test cases, the first line contains an integer n, meaning the number of shells in this shell necklace, where 1≤n≤105. Following line is a sequence with nnon-negative integer a1,a2,…,an, and ai≤107 meaning the number of schemes to decorate i continuous shells together with a declaration of love.
For each test cases, the first line contains an integer n, meaning the number of shells in this shell necklace, where 1≤n≤105. Following line is a sequence with nnon-negative integer a1,a2,…,an, and ai≤107 meaning the number of schemes to decorate i continuous shells together with a declaration of love.
Output
For each test case, print one line containing the total number of schemes module 313(Three hundred and thirteen implies the march 13th, a special and purposeful day).
Sample Input
3
1 3 7
4
2 2 2 2
0
Sample Output
14
54
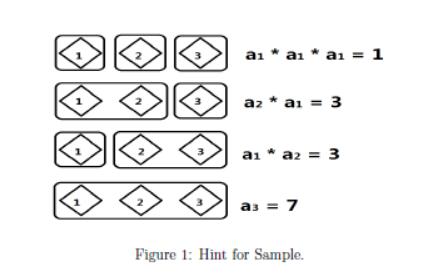 For the first test case in Sample Input, the Figure 1 provides all schemes about it. The total number of schemes is 1 + 3 + 3 + 7 = 14.
For the first test case in Sample Input, the Figure 1 provides all schemes about it. The total number of schemes is 1 + 3 + 3 + 7 = 14.
Hint
 For the first test case in Sample Input, the Figure 1 provides all schemes about it. The total number of schemes is 1 + 3 + 3 + 7 = 14.
For the first test case in Sample Input, the Figure 1 provides all schemes about it. The total number of schemes is 1 + 3 + 3 + 7 = 14.
Author
HIT
Source
Recommend
wange2014
一段长为x的项链作为一个整体,有a[x]种装饰方案。可以把不同的整体连接起来。问长为n的项链共有多少种方案。
动态规划 分治FFT
设f[i]为长为i的方案数,很明显 $ f[i]=sum_{j=1}^{i} a[j]*f[i-j] $
模数是313,这数的原根是啥啊?不知道。模数这么小,用FFT就可以了。
PS1 注意读入a[]的时候就要顺手取模,不然很容易乘爆炸
PS2 我也不知道为什么我要多输出一个换行符,白WA了三次才看到
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #define LL long long 7 using namespace std; 8 const double pi=acos(-1.0); 9 const int mod=313; 10 const int mxn=200010; 11 int read(){ 12 int x=0,f=1;char ch=getchar(); 13 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 14 while(ch>='0' && ch<='9'){x=x*10-'0'+ch;ch=getchar();} 15 return x*f; 16 } 17 struct com{ 18 double x,y; 19 com operator + (const com &b){return (com){x+b.x,y+b.y};} 20 com operator - (const com &b){return (com){x-b.x,y-b.y};} 21 com operator * (const com &b){return (com){x*b.x-y*b.y,x*b.y+y*b.x};} 22 com operator / (const double v){return (com){x/v,y/v};} 23 }a[mxn<<2],b[mxn<<2]; 24 int N,len,rev[mxn<<2]; 25 void FFT(com *a,int flag){ 26 for(int i=0;i<N;i++)if(i<rev[i])swap(a[i],a[rev[i]]); 27 for(int i=1;i<N;i<<=1){ 28 com wn=(com){cos(pi/i),flag*sin(pi/i)}; 29 int p=i<<1; 30 for(int j=0;j<N;j+=p){ 31 com w=(com){1,0}; 32 for(int k=0;k<i;k++,w=w*wn){ 33 com x=a[j+k],y=w*a[j+k+i]; 34 a[j+k]=x+y; 35 a[j+k+i]=x-y; 36 } 37 } 38 } 39 if(flag==-1) 40 for(int i=0;i<N;i++)a[i].x/=N; 41 return; 42 } 43 int n,w[mxn]; 44 LL f[mxn]; 45 void solve(int l,int r){ 46 if(l==r){(f[l]+=w[l])%=mod;return;} 47 int mid=(l+r)>>1; 48 solve(l,mid); 49 int i,j,m=(r-l+1); 50 for(N=1,len=0;N<=m;N<<=1)++len; 51 for(i=0;i<N;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(len-1)); 52 // 53 for(i=l;i<=mid;i++){a[i-l]=(com){f[i],0};} 54 for(i=mid-l+1;i<N;i++)a[i]=(com){0,0}; 55 for(i=0;i<N;i++)b[i]=(com){w[i+1],0}; 56 // 57 FFT(a,1);FFT(b,1); 58 for(i=0;i<N;i++)a[i]=a[i]*b[i]; 59 FFT(a,-1); 60 for(i=mid+1;i<=r;i++){ 61 (f[i]+=((LL)(a[i-l-1].x+0.5))%mod)%=mod; 62 } 63 solve(mid+1,r); 64 return; 65 } 66 int main(){ 67 int i,j; 68 while(scanf("%d",&n)!=EOF && n){ 69 memset(f,0,sizeof f); 70 for(i=1;i<=n;i++)w[i]=read()%mod;// 71 solve(1,n); 72 printf("%lld ",f[n]%mod); 73 } 74 return 0; 75 }