| Time Limit: 3000MS | Memory Limit: 30000K | |
| Total Submissions: 1020 | Accepted: 407 |
Description
Yoko's math homework today was to calculate areas of polygons in the xy-plane. Vertices are all aligned to grid points (i.e. they have integer coordinates).
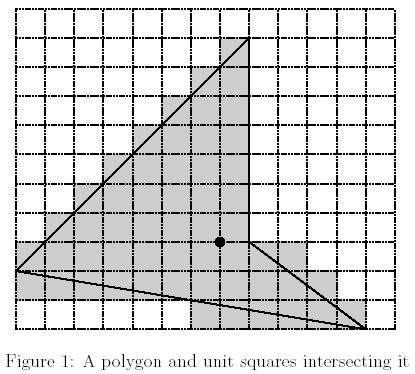
Your job is to help Yoko, not good either at math or at computer programming, get her homework done. A polygon is given by listing the coordinates of its vertices. Your program should approximate its area by counting the number of unit squares (whose vertices are also grid points) intersecting the polygon. Precisely, a unit square "intersects the polygon" if and only if the intersection of the two has non-zero area. In the figure below, dashed horizontal and vertical lines are grid lines, and solid lines are edges of the polygon. Shaded unit squares are considered intersecting the polygon. Your program should output 55 for this polygon (as you see, the number of shaded unit squares is 55).
Your job is to help Yoko, not good either at math or at computer programming, get her homework done. A polygon is given by listing the coordinates of its vertices. Your program should approximate its area by counting the number of unit squares (whose vertices are also grid points) intersecting the polygon. Precisely, a unit square "intersects the polygon" if and only if the intersection of the two has non-zero area. In the figure below, dashed horizontal and vertical lines are grid lines, and solid lines are edges of the polygon. Shaded unit squares are considered intersecting the polygon. Your program should output 55 for this polygon (as you see, the number of shaded unit squares is 55).

Input
The input file describes polygons one after another, followed by a terminating line that only contains a single zero.
A description of a polygon begins with a line containing a single integer, m (>= 3), that gives the number of its vertices. It is followed by m lines, each containing two integers x and y, the coordinates of a vertex. The x and y are separated by a single space. The i-th of these m lines gives the coordinates of the i-th vertex (i = 1,...,m). For each i = 1,...,m-1, the i-th vertex and the (i+1)-th vertex are connected by an edge. The m-th vertex and the first vertex are also connected by an edge (i.e., the curve is closed). Edges intersect only at vertices. No three edges share a single vertex (i.e., the curve is simple). The number of polygons is no more than 100. For each polygon, the number of vertices (m) is no more than 100. All coordinates x and y satisfy -2000 <= x <= 2000 and -2000 <= y <= 2000.
A description of a polygon begins with a line containing a single integer, m (>= 3), that gives the number of its vertices. It is followed by m lines, each containing two integers x and y, the coordinates of a vertex. The x and y are separated by a single space. The i-th of these m lines gives the coordinates of the i-th vertex (i = 1,...,m). For each i = 1,...,m-1, the i-th vertex and the (i+1)-th vertex are connected by an edge. The m-th vertex and the first vertex are also connected by an edge (i.e., the curve is closed). Edges intersect only at vertices. No three edges share a single vertex (i.e., the curve is simple). The number of polygons is no more than 100. For each polygon, the number of vertices (m) is no more than 100. All coordinates x and y satisfy -2000 <= x <= 2000 and -2000 <= y <= 2000.
Output
The output should consist of as many lines as the number of polygons. The k-th output line should print an integer which is the area of the k-th polygon, approximated in the way described above. No other characters, including whitespaces, should be printed.
Sample Input
4 5 -3 1 0 1 7 -7 -1 3 5 5 18 5 5 10 3 -5 -5 -5 -10 -18 -10 5 0 0 20 2 11 1 21 2 2 0 0
Sample Output
55 41 41 23
Source
Japan 2003,Aizu
数学问题 几何 扫描线
看到题面心惊胆战,看到数据范围发现就是个暴力扫描线。
维护一条扫描线从x轴最左边往最右边移动,对于每一列记录原图形上线段和扫描线的交点纵坐标。
将交点坐标用floor和ceil取整,就可以愉快地做线段覆盖了。
注意计算交点时候,要先乘后除。先除后乘会被卡精度。
日常犯蠢WA一串,身败名裂。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 const int mxn=405; 8 int read(){ 9 int x=0,f=1;char ch=getchar(); 10 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 11 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 12 return x*f; 13 } 14 struct point{ 15 double x,y; 16 point(){} 17 point(double _x,double _y):x(_x),y(_y){} 18 }p[mxn]; 19 struct Seg{point s,t;}L[mxn]; 20 double F(const point &a,const point &b,double x){ 21 return a.y+(b.y-a.y)*(x-a.x)/(b.x-a.x); 22 } 23 struct Line{ 24 double L,R; 25 bool operator < (const Line &b)const{ 26 return (L==b.L && R<b.R) || (L<b.L); 27 } 28 }s[mxn<<1]; 29 int sct=0; 30 int ans=0; 31 void solve(){ 32 sort(s+1,s+sct+1); 33 int last=-1e10; 34 for(int i=1;i<sct;i+=2){ 35 int x=floor(min(min(s[i].L,s[i+1].L),min(s[i].R,s[i+1].R))); 36 int y=ceil(max(max(s[i].L,s[i+1].L),max(s[i].R,s[i+1].R))); 37 if(x>=last)ans+=y-x; 38 else if(y>last)ans+=y-last; 39 last=y; 40 } 41 return; 42 } 43 int n; 44 int main(){ 45 int i,j; 46 while(scanf("%d",&n)!=EOF && n){ 47 ans=0; 48 int sx=1e8,mx=-1e8; 49 for(i=1;i<=n;i++){ 50 p[i].x=read();p[i].y=read(); 51 sx=min(sx,(int)p[i].x);mx=max(mx,(int)p[i].x); 52 } 53 p[n+1]=p[1]; 54 for(i=1;i<=n;i++){//segment 55 if(p[i].x<p[i+1].x){L[i].s=p[i];L[i].t=p[i+1];} 56 else{L[i].s=p[i+1];L[i].t=p[i];} 57 } 58 for(i=sx;i<mx;i++){ 59 sct=0; 60 for(j=1;j<=n;j++){ 61 if(L[j].s.x<=i && L[j].t.x>=i+1){ 62 ++sct; 63 s[sct].L=F(L[j].s,L[j].t,i); 64 s[sct].R=F(L[j].s,L[j].t,i+1); 65 if(s[sct].L>s[sct].R)swap(s[sct].L,s[sct].R); 66 } 67 } 68 solve(); 69 } 70 printf("%d ",ans); 71 } 72 return 0; 73 }