看标题不知道大家有没有想起小学做的七桥问题
一笔画问题主要包括欧拉路,欧拉回路,哈密尔顿通路,哈密尔顿回路
欧拉路
定义:无向图 G 中一条从 S 到 T 的路径不重不漏地经过了 G 中的每条边,称这条路径为欧拉路
其实欧拉路就是让你判断能否从一个点到另一个点,每条边只经过一次且经历所有的边的问题,其中对起点终点不做要求,对经过几次相同的点不做要求
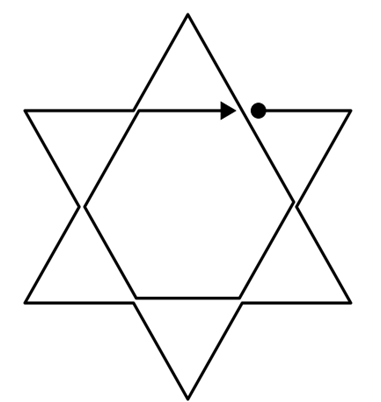 ·
· 
比如这两个图就存在欧拉路(可能有多种走法)
那么怎么判断是否存在欧拉路呢?
全部的点中只有两个点的度数为奇数,其他点的度数为偶数 ---欧拉
证明:
考虑起点,可能会经过多次,但最后一次一定是出去了,但不回来,终点类似
考虑其他点,都是进来一次出去一次
程序实现:
我们把一个度数为奇数的点作为起点,开始dfs,经过一条边删一条边,那么只要有边就会一直dfs下去,如果先遍历到了终点,回溯即可,回溯的时候并把点加入栈里,最后输出整个栈中的元素
看一个板子题
Luogu P2731 [USACO3.3]骑马修栅栏 Riding the Fences
题意还是比较好理解的
坑点就是有多组解时,输出第一位较小的。就是说在满足解的情况下,前面的数尽可能小
因为我们使用的是dfs所以先遍历的元素会较晚被放进栈中,所以我们让先遍历的元素尽可能小就好了,如果是欧拉回路,把起点设为1

1 /* 2 Work by: Suzt_ilymtics 3 */ 4 #include<iostream> 5 #include<cstdio> 6 using namespace std; 7 const int MAXN = 501; 8 int m, wz = 1; 9 int e[MAXN][MAXN], du[MAXN]; 10 int s[2048], sc = 0; 11 12 void dfs(int u){ 13 for(int i = 1; i <= 500; ++i){ 14 if(e[u][i]){ 15 e[u][i]--, e[i][u]--, dfs(i); 16 } 17 } 18 s[++sc] = u; 19 } 20 21 int main() 22 { 23 scanf("%d", &m); 24 for(int i = 1, u, v; i <= m; ++i){ 25 scanf("%d%d", &u, &v); 26 e[u][v]++;e[v][u]++; 27 du[u]++;du[v]++; 28 } 29 int cnt1 = 0, cnt2 = 0; 30 for(int i = 500; i >= 1; --i){ 31 if(du[i] % 2) cnt1++, wz = i; 32 else cnt2++; 33 } 34 dfs(wz); 35 while(sc) 36 printf("%d ", s[sc--]); 37 38 return 0; 39 }
欧拉回路
定义:无向图 G 中一条从 S 到 S 的路径不重不漏地经过了 G 中的每条边,称这条路为欧拉回路
含有欧拉路的图叫欧拉图,不含欧拉路的图叫半欧拉图
同欧拉路的区别就是把终点改成起点而已,其他没什么变化
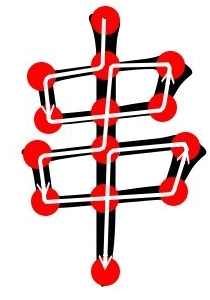
比如这就是两个欧拉回路
怎样的图存在欧拉回路?
全部点的度数为偶数
证明:
起点和终点是同一个点,即出去还要回来,所以为偶,其他点上面已经解释过了
怎么求?
和欧拉路一样。。。
起点随便定,dfs就好
例题:P1341 无序字母对
虽然题目中说是字母,但ASCLL码是个好东西,直接强制转整形存即可(就像上面的骑马修栅栏)
注意处理的几个点:
1、输出顺序(和修栅栏一样处理)
2、如果是欧拉回路,第一个点不一定是a
3、如果既不是欧拉路,也不是欧拉回路那就No Solution

1 /* 2 Work by: Suzt_ilymtics 3 */ 4 #include<iostream> 5 #include<cstdio> 6 using namespace std; 7 const int MAXN = 501; 8 int m, wz1, wz2; 9 char uu, vv; 10 int u, v; 11 int e[MAXN][MAXN], du[MAXN]; 12 int s[2048], sc = 0; 13 14 void dfs(int u){ 15 for(int i = 1; i <= 500; ++i){ 16 if(e[u][i]){ 17 e[u][i]--, e[i][u]--, dfs(i); 18 } 19 } 20 s[++sc] = u; 21 } 22 23 int main() 24 { 25 scanf("%d", &m); 26 for(int i = 1; i <= m; ++i){ 27 cin>>uu>>vv; 28 u = (int) uu; 29 v = (int) vv; 30 // cout<<u<<" "<<v<<endl; 31 e[u][v]++;e[v][u]++; 32 du[u]++;du[v]++; 33 } 34 int cnt1 = 0, cnt2 = 0; 35 for(int i = 500; i >= 1; --i){//样例是个环, 所以没有奇数点 36 if(du[i] % 2) cnt1++, wz1 = i; 37 else cnt2++; 38 if(du[i]) wz2 = i; 39 } 40 if(cnt1 == 2) dfs(wz1); 41 else if(cnt1 == 0) dfs(wz2); 42 else { 43 printf("No Solution"); return 0; 44 } 45 46 while(sc) 47 printf("%c", (char)s[sc--]); 48 49 return 0; 50 }
有向图的欧拉(回)路
上面我们在说的时候都是无向图,那有向图呢?
怎样的有向图存在欧拉路?
有两个点,一个点入度比出度多一,另一个点出度比入度多一,其余的点入度等于出度。
欧拉回路呢?
所有的点的出度等于入度
哈密尔顿通路
定义:无向图 G 中一条从 S 到 T 的路径不重不漏地经过所有的顶点,那么称条路径为哈密尔顿通路。
解释一下就是从一个点出发到另一个点,每个点只经过一次且每个点都要被经过,对边不做要求
去掉下图中的一条边就是哈密尔顿通路
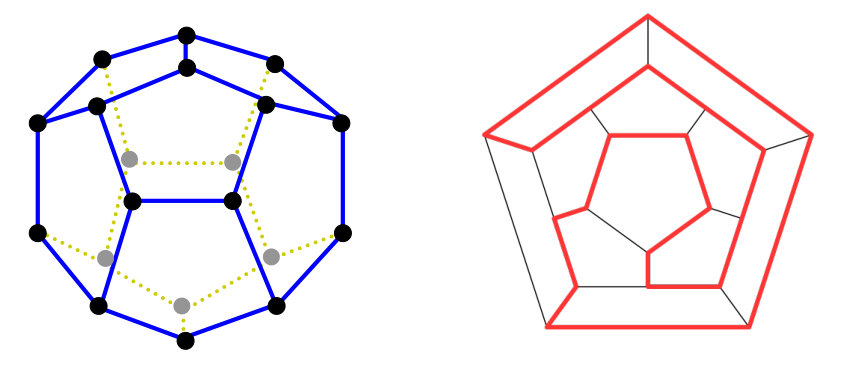
怎么求?
枚举起点和终点,在这之间加一条边,转化为哈密尔顿回路的问题
N阶竞赛图:
含有 N 个顶点的有向图,且每对顶点之间都有一条边。对于 N 阶竞赛图一定存在哈密尔顿通路
证明:
N = 2 时显然是成立的。
设 N = k 时是成立的,考虑证明 N = k + 1 时是成立的,设哈密尔顿路径为$V_1,V_2,…,V_k$
从k到1去找($V_i,V_k+1$)这样一条边,如果找到了那么形成$V_1,V_2,…V_i,V_k+1,V_i+1…,V_k$,这样一条通路。
否则形成$V_k+1,V_1,V_2,…,V_k$,这样一条通路
显然就是模拟上述过程,可能看代码会更清晰一点

1 /* 2 Work by: Suzt_ilymics 3 Knowledge: 竞赛图中的哈密尔顿通路 4 Time: 貌似是O(n^3) 5 */ 6 #include<iostream> 7 #include<cstdio> 8 using namespace std; 9 int n, ans[1010], now; 10 bool e[1010][1010]; 11 12 void ins(int pos, int k){//暴力插入 13 int temp; 14 now++; 15 for(int i = pos; i < now; ++i){ 16 temp = ans[i], ans[i] = k, k = temp; 17 } 18 } 19 20 void hamillton(){ 21 now = 2; ans[1] = 1;//now表示现在前几个元素构成了hamillton通路 22 for(int i = 2; i <= n; ++i){ 23 bool flag = false; 24 for(int j = now - 1; j >= 1; --j){ 25 if(e[ans[j]][i]){//如果从现有的元素中找到一个指出去的hamillton通路 26 flag = true; 27 ins(j+1, i);//就将他插进去 28 break; 29 } 30 } 31 if(!flag) ins(1, i);//如果没找到,就插到最前面 32 } 33 } 34 35 int main() 36 { 37 scanf("%d", &n); 38 for(int i = 1, u, v; i <= (n * (n - 1)) / 2; ++i){ 39 scanf("%d%d", &u, &v); 40 if(u < v) e[u][v] = 1;//我们只记录指出来的边 41 } 42 hamillton(); 43 for(int i = 1; i <= n; ++i){ 44 printf("%d ", ans[i]); 45 } 46 return 0; 47 }
哈密尔顿回路
定义:无向图 G 中一条从 S 到 S 的路径不重不漏的的经过除 S 外所有的顶点并且S 只经过了两次,那么称这条路径为哈密尔顿回路。
解释一下,就是把起点改成终点,其他的同哈密尔顿通路
还是如下图:
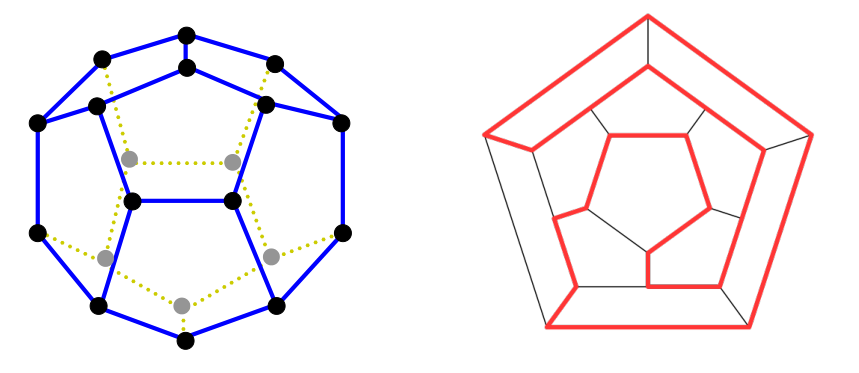
因为这是一个NPC问题(我也不太懂),所以它没有很好的判定定理,这里只给出一些充分条件和必要条件
必要条件:
定理一:
无向图$G { V , E }$ 哈密尔顿图,V1是V的任意非空子集,都有 P(G , V1) <= | V1 | ,其中 P (G , V1)表示图(G , V1)的联通分量数
证明:设 G 中地哈密尔顿回路为C,那么P(G,V1) <= P(C-V1)。因为C 是 G 的一个子图,往图中加边不会增加强连通分量的数量。因此只需要证明 P(C - V1) <= |V1|即可
C是哈密尔顿回路,一定是个环,然后开始删点,在最优的情况下第一次删点使得不再是个环,但是没有增加强联通分量的个数,之后每次删点最多能使得连通分量个数加1,也就是最多有 |V1| 个连通分量,即P(C - V1)<=|V1|。
注意,必要条件只能判断一个图不是哈密尔顿图
 左图满足上述条件,但没有哈密尔顿回路
左图满足上述条件,但没有哈密尔顿回路
推论一:
无向图G{V,E}中存在哈密尔顿通路,V1是V的任意非空子集,都有 P(G - V1) <= |V1| + 1。
根据上面的证明这个也很好理解。
下面这三个图都不存在哈密尔顿通路,第一个删掉5个点后共7个连通分量,第二个删3个共4个,第三个删5个共6个,不满足上述推论,所以一定没有哈密尔顿通路

充分条件:
Dirac定理:(狄拉克,1953)
设 G 是无向简单图, |G| = (n >=3),若 G 中每个节点度数至少为n / 2 ,则 G 有哈密尔顿回路
Ore定理:(奥尔,1960)
设 G 是无向简单图,|G| =(n >= 3),若 G 中任意不相邻的两个点 u,v都满足 d(u) + d(v) >= n,则 G 有哈密尔顿回路。
Ore定理的推论:
…,|G| >= 2,…d(u) +d(v) >= n -1,则 G 是哈密尔顿图
最后感谢yu__xuan学姐的课件支持!
