LG 题解 P7345 【DSOI 2021】吟唱的金色花海

目录

• 吐槽几句
• Solution
• Code

题目传送

吐槽几句

私以为鄙人之题解略易之与其他两篇题解。

他们都写的太长了，那么多图根本看不下去，还是我的比较清晰，代码也十分好写。

Solution

主要思想就是二分。

首先题目给你了位置 ((x_0, y_0)) 和一个时间 (t)。

因为从某个起点 ((sx, sy)) 扩展 (t) 次后，((x_0,y_0)) 一定在它的边界上。

所以我们可以搞出这么一张图。

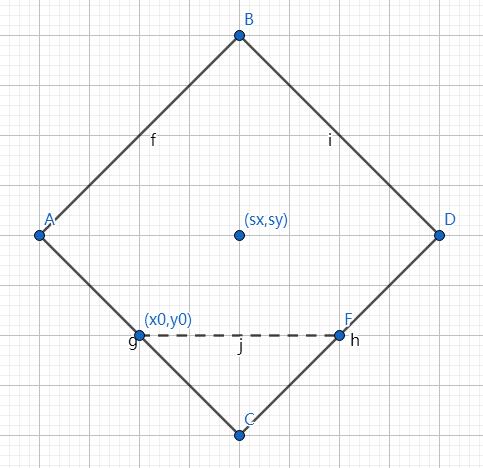
可能有的人看到这个图就瞬间明白了。下面再详细说一下。

根据这个图不难发现，我们只要找到 ((x_0,y_0)) 的一个（关于 BD）的对称点 (F)，然后它到中点的距离 (l) 可以求出，又因为我们知道了 ((x_0,y_0)) 和 ((sx,sy)) 的曼哈顿距离为 (t)，那我们就可以直接表示出 ((sx,sy))。

那么这个点 (F) 怎么求？想想那个 (MAX) 值为什么带了一个 (log)，就是让我们用二分啊。

因此这个 (F) 的特征就是最远的被染成金色的郁金香，我们可以二分 ((x_0,y_0)) 这个点向右走几步才能到达这个 (F)。

但是最远的时候是 (AD = 2t)，好像比需要的次数多 (1)。我们继续观察发现 ((x_0,y_0)) 与 (F) 的距离一定为偶数，所以二分的范围设为 ([1,t]) 即可。

需要注意我们还要确定的一个信息是延伸的方向，这个可以通过分别询问它的右边和下边是否是金色郁金香得到。

所以总的询问次数为 (log t + 2 le MAX)，可以通过。

实现细节看代码吧。

Code

/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int T, t, sx, sy, k;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int main()
{
    T = read();
    while(T--) {
        t = read(), sx = read(), sy = read(), k = read();
        if(t == 0) {
            printf("1 %d %d
", sx, sy)， fflush(stdout);
            continue;
        }
        int fx1, fx2, x; // 1 表示上左，2 表示下右 
        printf("0 %d %d
", sx + 1, sy)， fflush(stdout);
        x = read();
        if(x) fx1 = 1; else fx1 = -1;
        printf("0 %d %d
", sx, sy + 1)， fflush(stdout);
        x = read();
        if(x) fx2 = 1; else fx2 = -1; // 用 1/-1 方便后面的计算 
        int l = 1, r = t, ans = 0;
        while(l <= r) {
            int mid = (l + r) >> 1;
            printf("0 %d %d
", sx, sy + 2 * fx2 * mid)， fflush(stdout);
            x = read();
            if(x) ans = mid, l = mid + 1;
            else r = mid - 1;
        }
        int ex = sx, ey = sy + 2 * fx2 * ans; // 求得的 F 点 
        int Mid = (sy + ey) / 2;
        int ty = Mid, tx = sx + fx1 * (t - abs(Mid - ey)); // 直接求出终点 
        printf("1 %d %d
", tx, ty)， fflush(stdout);
    }
    return 0;
}