Prim:适合边稠密的图
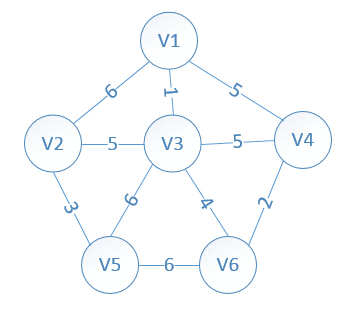
设置2个数据结构:MST lowcost
我们假设V1是起始点,进行初始化(lowcost[]==-1 代表 无通路 lowcost[i]==0代表 顶点 i 加入到MST 中):
V1 加入MST 比较 其余定点到 MST 内所有顶点的权值(即:其余顶点到V1)
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=-1,lowcost[6]=-1,明显看出,以V3为终点的边的权值最小=1,
V3 加入MST 比较 其余定点到 MST 内所有顶点的权值(即:其余顶点到V1,V3)
需要更新lowcost数组:
lowcost[2]=5,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
V6 加入MST 比较 其余定点到 MST 内所有顶点的权值(即:其余顶点到V1,V3,V6)
.。。。。。。。
直到所有点在MST内
dijkstra算法:适合边稀疏的图
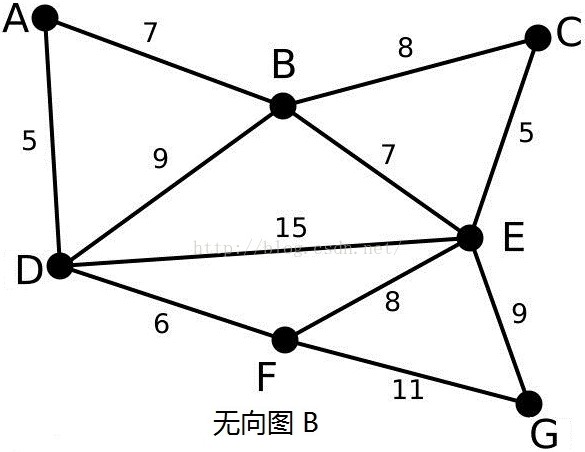
1. 把每个顶点放到集合 V 中
2. 找到图内权值最小的边<A,D>放到集合 E 中;在集合 V 内 标记 顶点A D,
边<A ,B>,<B,D>,<E,D>,<F,D>进行下一次的比较
3. 重复操作 2 直到集合 V 内所有顶点都被标记;按照 此时集合 E 内的边连接各个顶点 即可得到最小生成树