题目:
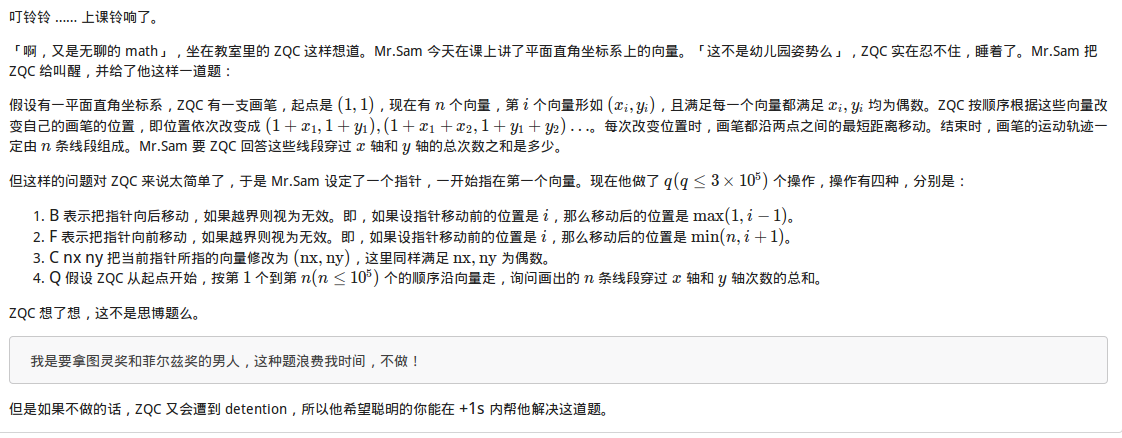
题解:
比较容易发现 : (x,y) 的贡献是独立的。
所以可以分开考虑。
假设我们考虑 (x).向量在 (x) 方向的投影依次是 : ({a_1,a_2, ... ,a_n})
那么在点 (i) 时候的 (x) 坐标即 : (1 + sum_{k=1}^ia_i),设 (s_i = sum_{k=1}^ia_i)
那么贡献即 : (sum_{i=1}^[(1+s_{i-1})*(1+s_i) < 0])
也就是 : (sum_{i=1}^n [max{s_i,s_{i-1}}>0 space space && space space min{s_i,s_{i-1}} < 0])
考虑容斥原理,我们可以得到 :
[n - sum_{i=1}^n[max{s_i,s_{i-1}}<0] - sum_{i=1}^n[min{s_i,s_{i-1}}>0]
]
还有 :
(sum_{i=1}^n [max{s_i,s_{i-1}}<0 space space && space space min{s_i,s_{i-1}} > 0]) (?)
不存在的
所以用 Splay 支持单点修改,区间加上一个数和统计小于/大于零的数的个数。
分别维护即可。
后来又去写才发现自己想简单了。
按照序列序插入做和按照权值插入做都不能简单的直接应用到全局。
正确的姿势是维护一个偏移量,表示插入到Treap中的点和实际上的点偏差了多少。
所以我们可以只将操作指针右侧的点全部插入到Treap中,并且在外面记录所有在Treap中的元素与实际的相差了多少。
怎么处理每个元素实际上的偏差并不是全局的偏差?
插入的时候让这个元素向反方向偏移一下再插入,然后就可以保证所有Trie中的元素偏移量都一样了。
对于所有指针左边的点,我们知道我们修改的时候不会对左边的东西造成任何影响。
所以可以直接维护终坐标和在这段时间内跨越坐标轴的次数。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef pair<int,int> pa;
inline void read(int &x){
x=0;static char ch;static bool flag;flag = false;
while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
#define mk(x,y) make_pair(x,y)
#define fst first
#define snd second
const int maxn = 100010;
struct Treap{
struct Node{
Node *ch[2];
int w,siz,fix;
void update(){
siz = ch[0]->siz + ch[1]->siz + 1;
}
}*root,mem[maxn],*it,*null;
Node *ws[maxn];int top;
inline void init(){
it = mem;null = it ++ ;
null->ch[0] = null->ch[1] = null;
null->siz = 0;null->fix = 0x3f3f3f3f;
root = null;
}
inline Node* newNode(int x){
Node *p = top ? ws[top--] : it ++ ;
p->ch[0] = p->ch[1] = null;
p->siz = 1;p->fix = rand();
p->w = x;return p;
}
inline void rotate(Node* &p,int k){
Node *x = p->ch[k^1];
p->ch[k^1] = x->ch[k];
x->ch[k] = p;
p->update();x->update();
p = x;return ;
}
void insert(Node* &p,int x){
if(p == null){
p = newNode(x);
return ;
}insert(p->ch[x >= p->w],x);
if(p->ch[x>=p->w]->fix < p->fix)
rotate(p,x<p->w);
p->update();
}
void erase(Node* &p,int x){
if(p->w == x){
if(p->ch[0] != null && p->ch[1] != null){
int k = p->ch[0]->fix < p->ch[1]->fix;
rotate(p,k);
erase(p->ch[k],x);
}else{
Node *y = p->ch[0] != null ? p->ch[0] : p->ch[1];
ws[++top] = p;p = y;
}
}else erase(p->ch[x >= p->w],x);
if(p != null) p->update();
}
inline void insert(int x){insert(root,x);}
inline void erase(int x){erase(root,x);}
inline int les(int x){
Node *p = root;
int res = 0;
while(p != null){
if(p->w > x) p = p->ch[0];
else res += p->ch[0]->siz + 1,p = p->ch[1];
}return res;
}
inline int gre(int x){
Node *p = root;
int res = 0;
while(p != null){
if(p->w < x) p = p->ch[1];
else res += p->ch[1]->siz + 1,p = p->ch[0];
}return res;
}
Treap(){init();}
}zsx[2],zsy[2];
pa a[maxn];
int X,Y,dx,dy,pot,n,ansx,ansy;
inline void move_right(){
if(pot == n) return ;++ pot;
zsx[0].erase(min(X-dx,X+a[pot].fst-dx));
zsy[0].erase(min(Y-dy,Y+a[pot].snd-dy));
zsx[1].erase(max(X-dx,X+a[pot].fst-dx));
zsy[1].erase(max(Y-dy,Y+a[pot].snd-dy));
if(X*(X+a[pot].fst) < 0) ++ ansx;
if(Y*(Y+a[pot].snd) < 0) ++ ansy;
X += a[pot].fst;Y += a[pot].snd;
}
inline void move_left(){
if(pot == 1) return ;
X -= a[pot].fst;Y -= a[pot].snd;
if(X*(X+a[pot].fst) < 0) -- ansx;
if(Y*(Y+a[pot].snd) < 0) -- ansy;
zsx[0].insert(min(X-dx,X+a[pot].fst-dx));
zsy[0].insert(min(Y-dy,Y+a[pot].snd-dy));
zsx[1].insert(max(X-dx,X+a[pot].fst-dx));
zsy[1].insert(max(Y-dy,Y+a[pot].snd-dy));
-- pot;
}
inline void modify(){
int x,y;read(x);read(y);
if(X*(X-a[pot].fst) < 0) -- ansx;
if(Y*(Y-a[pot].snd) < 0) -- ansy;
X += x - a[pot].fst;
Y += y - a[pot].snd;
dx += x - a[pot].fst;
dy += y - a[pot].snd;
a[pot] = mk(x,y);
if(X*(X-x) < 0) ++ ansx;
if(Y*(Y-y) < 0) ++ ansy;
}
inline int query(){
int res = n - pot - zsx[0].gre(-dx) - zsx[1].les(-dx) +
n - pot - zsy[0].gre(-dy) - zsy[1].les(-dy);
return res + ansx + ansy;
}
int main(){
srand(2619520);
int q;read(n);
X = Y = 1;
rep(i,1,n){
read(a[i].fst);read(a[i].snd);
zsx[0].insert(min(X,X+a[i].fst));
zsy[0].insert(min(Y,Y+a[i].snd));
zsx[1].insert(max(X,X+a[i].fst));
zsy[1].insert(max(Y,Y+a[i].snd));
X += a[i].fst;Y += a[i].snd;
}X = Y = 1;
move_right();read(q);
char ch;
while(q--){
while(ch=getchar(),ch<'!');
if(ch == 'B') move_left();
else if(ch == 'F') move_right();
else if(ch == 'C') modify();
else printf("%d
",query());
}
return 0;
}