#510. 「LibreOJ NOI Round #1」动态几何问题

---

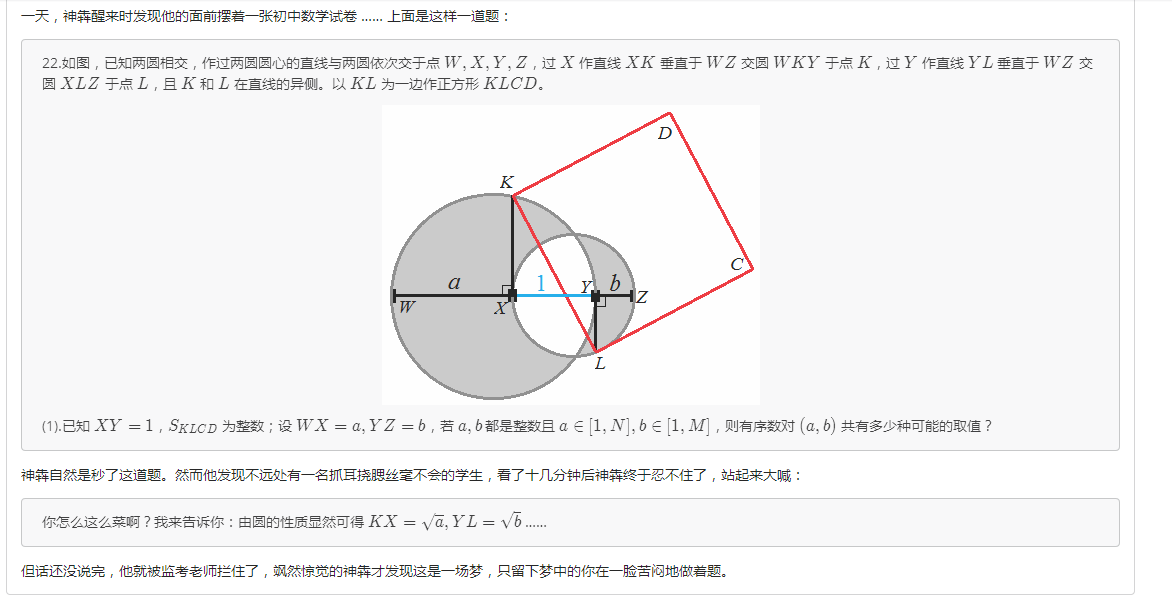
题目:

题解:

几何部分,先证明一下 (KX = sqrt{a},YL = sqrt{b})
设左侧的圆心为 (O) ,连接 (OK) ,我们有 (OK = r).
然后有 (r = frac{a+1}{2},OX = r - a)
勾股定理有 : (KX^2 = OK^2 + OX^2) 解得 : (KX = sqrt{a}).
同理 : (YL = sqrt{b}).
然后我们将 (YL) 向左平移直到 (b) 与 (X) 重合,设此时点 (L) 所在处为 (N).
那么有 : (KN^2 + NL^2) 是整数.
整理可得 : (sqrt{ab}) 是整数.

那么现在的问题就是问有多少有序数对 ((a,b)) 满足 (a in [1,n],b in [1,m] 且 sqrt{ab} 是整数)
对于 (a) 这个数字，我们考虑把它拆开 : 令 (a = a_1^2*a_2)
其中 (a_2) 不含平方因子.
对于 (b_2) 同样的拆成 (b = b_1^2*b_2)
那么我们发现原来的式子变成了 (a_1b_1sqrt{a_2b_2})
因为两个不含平方因子的数的乘积变成一个完全平方数，所以易得 (a_2 = b_2) , 设为 (d).
所以我们可以枚举 (1space .. n) 的 (d) ，只要我们保证 (d) 不含平方因子即可.
那么对于一个确定的 (d) ,由于我们知道 (d*a_1^2 leq n)所以有 (a_1^2 leq lfloor frac{n}{d} floor)
那么我们知道对于 (n) 以内的完全平方数一共有 (lfloor sqrt{n} floor) 个。
那么我们就知道对于一个确定的 (d) ,有 (lfloor sqrt{lfloor frac{n}{d} floor} floor) 个满足条件的 (a)。
那么我们发现计算式实际上就是 :

[sum_{i=1}^{min(n,m)}mu(i)^2 lfloor sqrt{lfloor frac{n}{d} floor} floor lfloor sqrt{lfloor frac{m}{d} floor} floor ]

然后我们考虑如何计算 (mu(i)^2).
我们通过意义来考虑，这实际上就是对是质因子平方倍数的数逐个筛去。
考虑容斥原理，然后用 (mu(i)) 做容斥系数。
我们发现有 : (sum_{i=1}^nmu(i)^2 = sum_{i=1}^{sqrt{n}}mu(i)lfloor frac{n}{i^2} floor)
我们可以提前线性筛出前 (sqrt{n}) 的 (mu) ,然后对于后面的 (sum) 式我们跳块求就好了.
可以证明 : (lfloor frac{n}{i^2} floor) 的不同值的数目不超过 (O(n^{frac{1}{3}})).

然后计算主计算式的时候后面的两部分也跳块就好了。

常数优越即 (AC) ,否则 (95).

#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(ll &x){
	x=0;static char ch;static bool flag;flag = false;
	while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
	while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
const int maxn = 124000000;
int pri[maxn/10],f[maxn],cnt,sqrn;
short mu[maxn];bool vis[maxn];
inline void liner(int n){
	mu[1] = f[1] = 1;
	rep(i,2,n){
		if(!vis[i]){
			pri[++cnt] = i;
			mu[i] = -1;
		}
		rep(j,1,cnt){
			ll x = 1LL*i*pri[j];
			if(x > n) break;
			vis[x] = true;
			if(i % pri[j] == 0) break;
			mu[x] = -mu[i];
		}
		f[i] = mu[i]*mu[i];
		mu[i] += mu[i-1];
		f[i] += f[i-1];
	}
}
map<ll,ll>g;
inline ll mu_2(ll n){
	if(n <= sqrn) return f[n];
	if(g.count(n)) return g[n];
	ll res = 0,i = 1;
	for(;i*i*i<=n;++i) res += n/(i*i)*(mu[i] - mu[i-1]);
	for(ll j,v;i*i <= n;i = j+1){
		j = sqrt(n / (v = (n / (i*i))) );
		res += (mu[j] - mu[i-1])*v;
	}return g[n] = res;
}
int main(){
	ll n,m;read(n);read(m);
	if(n > m) swap(n,m);
	liner(sqrn = sqrt(n));
	ll ans = 0,la = 0,tmp;
	for(ll i = 1,j,v1,v2;i <= n; i = j+1){
		v1 = sqrt(n / i);v2 = sqrt(m / i);
		j = min(n / (v1*v1),m / (v2*v2));
		ans += ((tmp = mu_2(j)) - la)*v1*v2;
		la = tmp;
	}printf("%lld
",ans);
	return 0;
}