核函数的作用就是隐含着一个从低维空间到高维空间的映射，而这个映射可以把低维空间中线性不可分的两类点变成线性可分的。
什么是线性不可分什么又是线性可分呢？
线性不可分简单来说就是你一个数据集不可以通过一个线性分类器（直线、平面）来实现分类。这样子的数据集在实际应用中是很常见的，例如：人脸图像、文本文档等，通过一刀切的方式你会发现除非这个刀是一个不规则的形状，不然很难分。
在二维空间中，要分开两个线性可分的点集合，我们需要找到一条分类直线即可 ，这就是线性可分
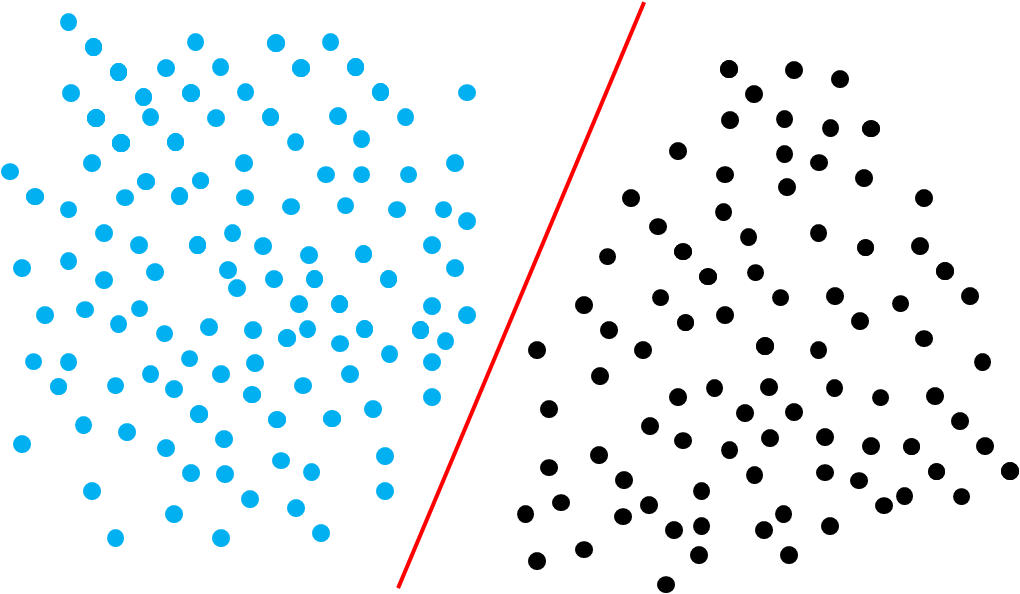
在n维空间中，要分开两个线性可分的点集合，我们需要找到一个超平面。
核函数可以把低维的变成高位
下面这张图位于第一、二象限内。我们关注红色的门，以及“北京四合院”这几个字下面的紫色的字母。我们把红色的门上的点看成是“+”数据，紫色字母上的点看成是“-”数据，它们的横、纵坐标是两个特征。显然，在这个二维空间内，“+”“-”两类数据不是线性可分的。
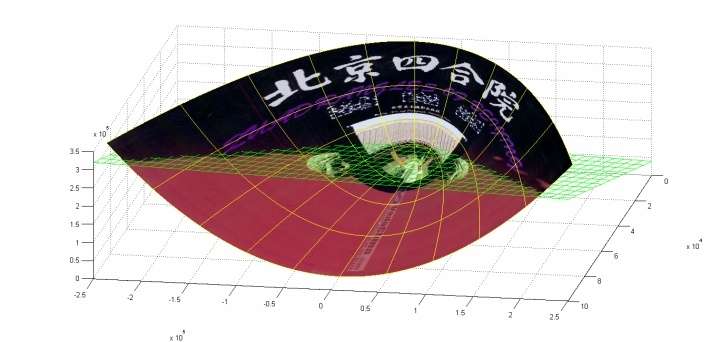
注意到绿色的平面可以完美地分割红色和紫色，也就是说，两类数据在三维空间中变成线性可分的了。
而三维中的这个判决边界，再映射回二维空间中是这样的：
这是一条双曲线，它不是线性的。
所以我对核函数的理解就是把一个本来不是很明显的有需求的东西变成一个明显的满足需求的东西的一个工具。多变少。
核函数和映射没有关系。核函数只是用来计算映射到高维空间之后的内积的一种简便方法。
现实生活中有很多非线性非常强的特征 而核方法能够捕捉它们