逻辑回归是一个分类的问题,结果要么是0要么是1
书本中提到一个例子就是判断肿瘤是否是良性还是恶性的,但其实在我看来,0和1是组成一切的单元基,正如我们目前使用的电脑中能看到一切都能转换为0和1,判断房子的价格也可以,可以先判断房子是否有卧室等各种条件,如果有就可以对应的增加一定的价值,最后推出房子的价格
接着书中引入了一个s型函数,它其实只是一个合理化的选择,针对不同的模型其实可以用自己来定义个喜欢的类似s的函数。它的作用只是将一些属性转化为对于0和1有用的区间,如果我们喜欢可以直接把1000除以10000,得到0.1。只是这样看起来不太合理经此而已。
另外一个问题是书本中的图都是平面的或者立体的,它的维度停留在3维以下,但其实如果面对很高很高维度的问题的时候,例如房子是否能卖出去,这种问题的时候,我觉得可以提取维度,把一些属性通过一定的方式合并成为一个维度,这样可能更加有利于画图理解。
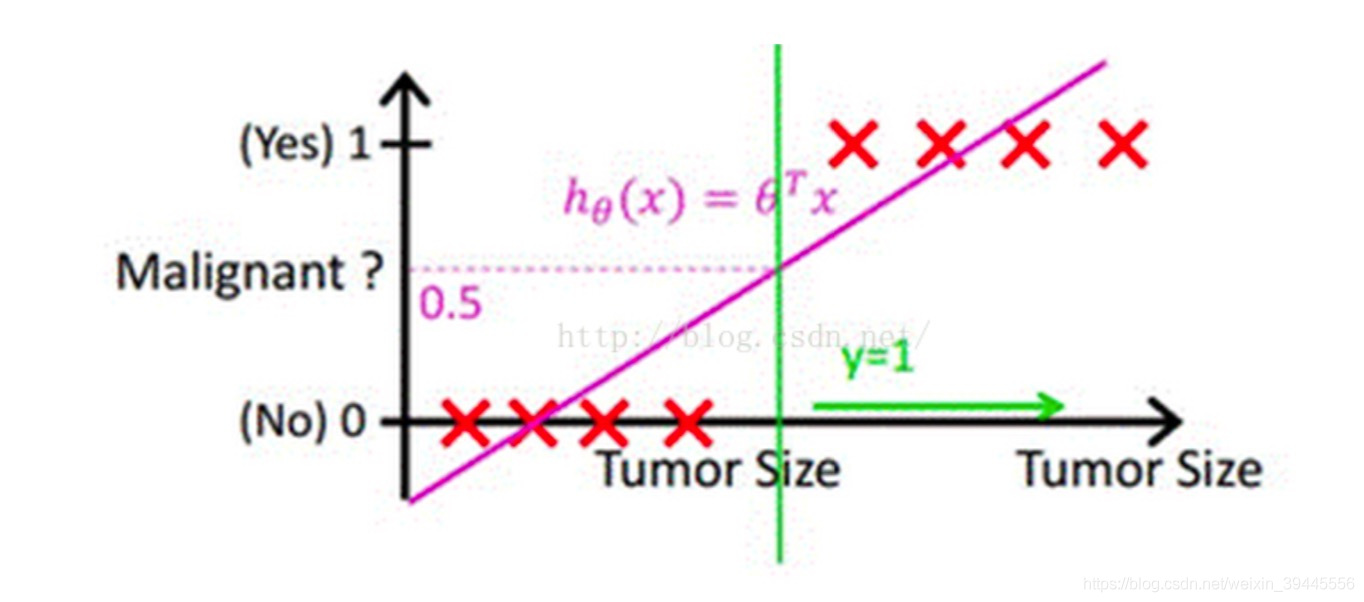
像这种图你很容易找到一个模型是适应他,或者说你一看图心里面就知道怎么做
但是如果是一个很难表示出来的图呢?(1X是点,2X是线,3X则是一个面了,那么4X呢?)其实这些做法的本质只是将一些属性关联起来,并给以一个权重。最后让输出的结果在0~1之间。
这样看起来就很和线性回归相似了
接下来就是要解决一个评定模型好或者不好了,这边依然是使用一个叫代价函数的东西,但是这边的hθ是和线性中一样的,他是分母为变量,书上说它是一个非凸函数,我的理解是因为

θ是一个[055,6,4,8,4,5,5,6]类似这样的,乘上x([1,0.1,888,6666666....])最后输出的结果是一个负无穷到正无穷的值,经过s函数的优化之后才成为0~1。而其实他的变量变化并不是线性的。因为0.7可以被看作是1,0.4可以被看作0。
所以需要让0.7等于0.7,0.4等于0.4,或者让他0.7=7,0.4=4。所以要让代价函数是一个凸函数。
书中引入的是一个log,其实意思应该和我想的是一样的,保持输出结果的真正含义,0.7就是0.7,不能因为经过了s函数就变成了1。也就是说解决这个问题可以在训练的时候不加入s函数,让它同线性问题一样,自然的进行,在需要预测的时候再加入s函数。
接下来就是和线性回归一样了,一个权重对应一个变化,for i in all,一个个迭代更新。