归并排序 冯诺依曼发明的一个算法。分治为其中的核心思想。这个排序的时间复杂度为O(nlogn)
归并排序的流程图:
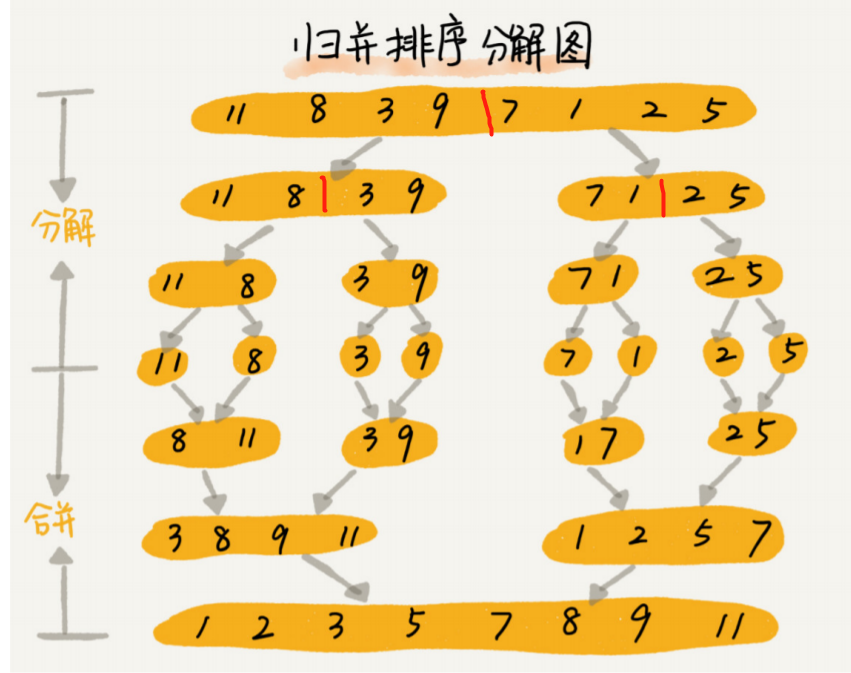
整体的流程图如下:

这个算法的特点:
平均时间复杂度:O(nlogn)
最佳时间复杂度:O(n)
最差时间复杂度:O(nlogn)
空间复杂度:O(n)
排序方式:In-place
稳定性:稳定
不管元素在什么情况下都要做这些步骤,所以花销的时间是不变的,所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为:O( nlogn ),因为都需要进行拆分。
public static void merge_sort(int[] arr) {
int len = arr.length;
int[] result = new int[len];
int block, start;
for(block = 1; block < len*2; block *= 2) {
for(start = 0; start <len; start += 2 * block) {
int low = start;
int mid = (start + block) < len ? (start + block) : len;
int high = (start + 2 * block) < len ? (start + 2 * block) : len;
//两个块的起始下标及结束下标
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
//开始对两个block进行归并排序
while (start1 < end1 && start2 < end2) {
result[low++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
}
while(start1 < end1) {
result[low++] = arr[start1++];
}
while(start2 < end2) {
result[low++] = arr[start2++];
}
}
int[] temp = arr;
arr = result;
result = temp;
}
result = arr;
}
递归的写法的难点就是找到节奏,还有一个写时候的细节就是奇数情况下如何进行思考。