堆排序（选择排序）-八大排序汇总（2）

二叉堆的定义

二叉堆是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆。下图展示一个最小堆：

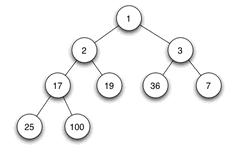
堆的存储

一般都用数组来表示堆，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。

堆的操作——插入删除

下面先给出《数据结构C++语言描述》中最小堆的建立插入删除的图解。

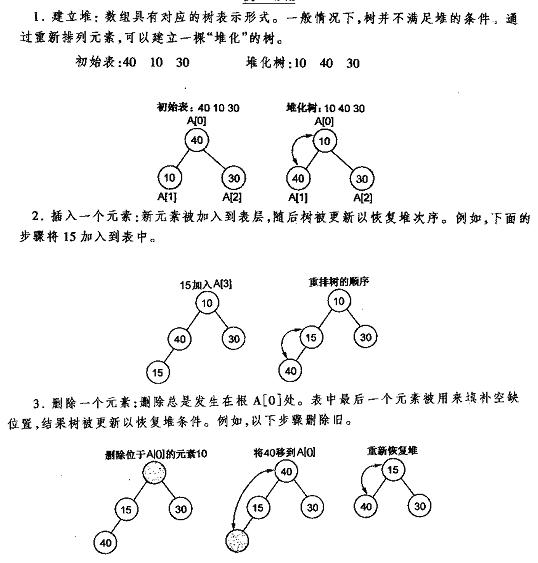
堆的插入

每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。

//  新加入i结点  其父结点为(i - 1) / 2
void MinHeapFixup(int a[], int i)
{
    int j, temp;
    
    temp = a[i];
    j = (i - 1) / 2;      //父结点
    while (j >= 0 && i != 0)
    {
        if (a[j] <= temp)
            break;
        
        a[i] = a[j];     //把较大的子结点往下移动,替换它的子结点
        i = j;
        j = (i - 1) / 2;
    }
    a[i] = temp;
}

更简短的表达为：

void MinHeapFixup(int a[], int i)
{
    for (int j = (i - 1) / 2; (j >= 0 && i != 0)&& a[i] > a[j]; i = j, j = (i - 1) / 2)
        Swap(a[i], a[j]);
}

插入时：

//在最小堆中加入新的数据nNum
void MinHeapAddNumber(int a[], int n, int nNum)
{
    a[n] = nNum;
    MinHeapFixup(a, n);
}

堆的删除

按定义，堆中每次都只能删除第0个数据。为了便于重建堆，实际的操作是将最后一个数据的值赋给根结点，然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的，如果父结点比这个最小的子结点还小说明不需要调整了，反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。下面给出代码：

//  从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
    int j, temp;

    temp = a[i];
    j = 2 * i + 1;
    while (j < n)
    {
        if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
            j++;

        if (a[j] >= temp)
            break;

        a[i] = a[j];     //把较小的子结点往上移动,替换它的父结点
        i = j;
        j = 2 * i + 1;
    }
    a[i] = temp;
}
//在最小堆中删除数
void MinHeapDeleteNumber(int a[], int n)
{
    Swap(a[0], a[n - 1]);
    MinHeapFixdown(a, 0, n - 1);
}

堆化数组

有了堆的插入和删除后，再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧，不用！先看一个数组，如下图：

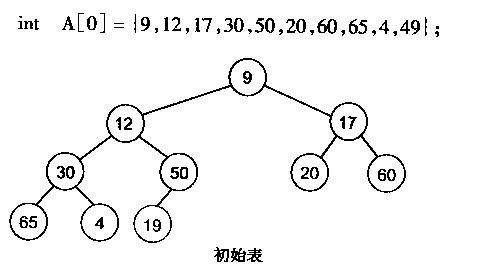
很明显，对叶子结点来说，可以认为它已经是一个合法的堆了即20，60， 65， 4， 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30，A[2] = 17，A[1] = 12，A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤：

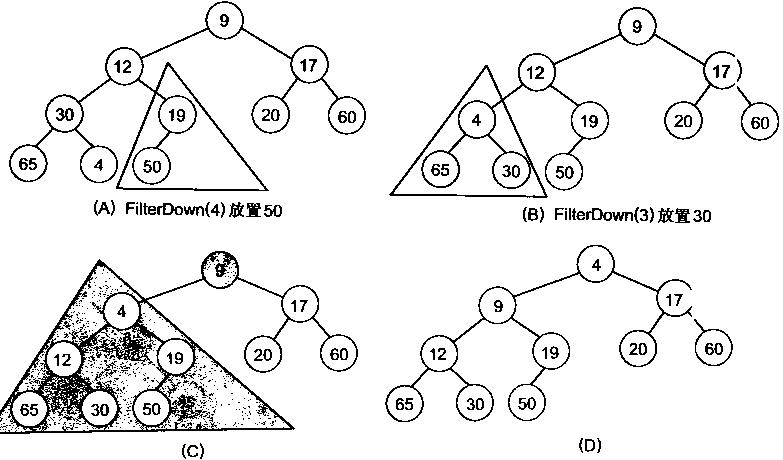
写出堆化数组的代码：

//建立最小堆
void MakeMinHeap(int a[], int n)
{
    for (int i = n / 2 - 1; i >= 0; i--)
        MinHeapFixdown(a, i, n);
}

至此，堆的操作就全部完成了(注1)，再来看下如何用堆这种数据结构来进行排序。

堆排序

首先可以看到堆建好之后堆中第0个数据是堆中最小的数据。取出这个数据再执行下堆的删除操作。这样堆中第0个数据又是堆中最小的数据，重复上述步骤直至堆中只有一个数据时就直接取出这个数据。

由于堆也是用数组模拟的，故堆化数组后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。有点类似于直接选择排序。

void MinheapsortTodescendarray(int a[], int n)
{
    for (int i = n - 1; i >= 1; i--)
    {
        Swap(a[i], a[0]);
        MinHeapFixdown(a, 0, i);
    }
}

注意使用最小堆排序后是递减数组，要得到递增数组，可以使用最大堆。

基本思想

① 先将初始文件R[1..n]建成一个大根堆，此堆为初始的无序区

② 再将关键字最大的记录R[1]（即堆顶）和无序区的最后一个记录R[n]交换，由此得到新的无序区R[1..n-1]和有序区R[n]，且满足R[1..n-1].keys≤R[n].key

③由于交换后新的根R[1]可能违反堆性质，故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换，由此得到新的无序区R[1..n-2]和有序区R[n-1..n]，且仍满足关系R[1..n-2].keys≤R[n-1..n].keys，同样要将R[1..n-2]调整为堆。

……

直到无序区只有一个元素为止。

基本操作（大根堆）

①建堆，建堆是不断调整堆的过程，从len/2处开始调整，一直到第一个节点。建堆的过程是线性的过程，从len/2到0处一直调用调整堆的过程，相当于o(h1)+o(h2)…+o(hlen/2) 其中h表示节点的深度，len/2表示节点的个数，这是一个求和的过程，结果是线性的O(n)。

②调整堆：调整堆在构建堆的过程中会用到，而且在堆排序过程中也会用到。利用的思想是比较节点i和它的孩子节点left(i),right(i)，选出三者最大(或者最小)者，如果最大（小）值不是节点i而是它的一个孩子节点，那边交互节点i和该节点，然后再调用调整堆过程，这是一个递归的过程。调整堆的过程时间复杂度与堆的深度有关系，是lgn的操作，因为是沿着深度方向进行调整的。

③堆排序：堆排序是利用上面的两个过程来进行的。首先是根据元素构建堆。然后将堆的根节点取出(一般是与最后一个节点进行交换)，将前面len-1个节点继续进行堆调整的过程，然后再将根节点取出，这样一直到所有节点都取出。

稳定性

堆排序是不稳定的排序方法

时间复杂度：

调整堆的时间复杂度是lgn，调用了n-1次，所以堆排序过程的时间复杂度是O(nlgn)。

空间复杂度

堆排序是就地排序，辅助空间为O(1）

比较

用小根堆排序与利用大根堆类似，只不过其排序结果是递减有序的。堆排序和直接选择排序相反：在任何时刻堆排序中无序区总是在有序区之前，且有序区是在原向量的尾部由后往前逐步扩大至整个向量为止

注意

大根堆输出的是降序排列的数组，小根堆输出的是升序排列的数组。

代码

#include "stdafx.h"
#include <iostream>
using namespace std;

inline void Swap(int &a, int &b)
{
    int c = a;
    a = b;
    b = c;
}

inline void print(int a[], int n)
{
    for (int i = 0; i < n; i++)
    {
        if (i != n - 1)
        {
            cout << a[i] << ",";
        }
        else
            cout << a[i];
    }
    cout << endl;
}

//  从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2
void MinHeapFixdown(int a[], int i, int n)
{
    int j, temp;
    temp = a[i];
    j = 2 * i + 1;
    while (j < n)
    {
        if (j + 1 < n && a[j + 1] < a[j]) //在左右孩子中找最小的
            j++;
        if (a[j] >= temp)
            break;
        a[i] = a[j];     //把较小的子结点往上移动,替换它的父结点
        i = j;
        j = 2 * i + 1;
    }
    a[i] = temp;
}

//建立最小堆
void MakeMinHeap(int a[], int n)
{
    for (int i = n / 2 - 1; i >= 0; i--)
        MinHeapFixdown(a, i, n);
    print(a,10);
}

//最小堆排序
void MinheapsortTodescendarray(int a[], int n)
{
    for (int i = n - 1; i >= 1; i--)
    {
        Swap(a[i], a[0]);
        MinHeapFixdown(a, 0, i);
    }
    print(a, 10);
}

// 堆排序
void HeapSort(int a[],int n)
{
    MakeMinHeap(a, n);
    MinheapsortTodescendarray(a, n);
}

int _tmain(int argc, _TCHAR* argv[])
{
    int a[20] = {43,123,42,12,65,44,88,37,93,32};
    HeapSort(a, 10);
    system("pause");
    return 0;
}

比如数组a[]={6,5,4,3,2,1,0}

          6

　　　5  4

　　3  2 1 0

第一轮：i = n/2-1 = 2， a[2]=4，子节点为1和0,与较小的交换,i--

          6

　　  5    0

      3  2 1  4

第二轮：i = i-1 = 1, a[1]=5,子节点为3和2，与较小的交换

           6

        2     0

      3   5  1  4

第三轮：i = i-1 =0,a[0]=6,子节点为2和0，与较小的交换

            0

        2      6

      3   5   1  4

j = 2i+1=1,a[j]=6,子节点1和4，与较小的交换

            0

　　  2       1

     3    5   6   4

这时完成堆的构建,接下来进行堆的排序

第一轮：交换a[0]和a[i-1]

         4

      2      1

    3   5  6  0

从a[0]开始，与较小子节点交换

         1

      2     4

    3   5  6  0

第二轮：a[0]和a[i-2]交换

         6

      2      4

    3   5   1  0

恢复堆，从a[0]开始，与较小子节点交换

        2

     6     4

  3    5   1  0

继续

         2

     3       4

   6   5   1   0

第三轮：a[0]与a[i-3]交换

　　　 5

     3       4

   6   2   1  0

恢复堆，从a[0]开始，与较小节点交换

          3

      5      4

   6    2  1   0

第四轮：a[0]与a[i-4]交换

          6

       5    4

     3  2  1  0

恢复堆，从a[0]开始，与较小节点交换

         4

     5      6

   3  2   1  0

第五轮：a[0]与a[i-5]交换

        6

     5    4 

   3  2  1  0

恢复堆，从a[0]开始，与较小节点交换

        5

    6      4

  3   2  1   0

第六轮：a[0]与a[i-6]交换

　　   6

      5    4

    3  2 1  0

从而完成堆的排序

参考：http://blog.csdn.net/morewindows/article/details/6709644