2018.10.25 正睿停课训练 Day9
期望得分:100+60+20
实际得分:100+0+0
Dijkstra模板题爆零了。我还有救吗
A 数独(思路 DP)
先是想到,限制的是1,但其实在数独里1和2,3,...,9别的数没啥特殊的地方啊,可以忽略其它数的种类?
好,上面这句话没什么用。
考虑到每种合法的填1方案(不考虑其它数,先只填1),对数独的解数的贡献是一样的。
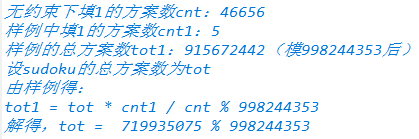
所以我们求 (当前填1合法方案数/无限制填1合法方案数) 这个比例,再乘以无限制的数独总解数就行了。
当前填1合法方案数可以DP,状压一下,三行三行转移,非常轻松。直接DFS也随便过。
数独总解数大概可以各种剪枝+优化(对称性)在本机跑出来。反正我选择百度。
搜索求解的数量(orz wph):

或者面向样例得到解的数量(orz wzh)
//49ms 504kb
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 100000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define mod 998244353
#define lb(x) (x&-(x))
#define Mod(x) x>=mod&&(x-=mod)
typedef long long LL;
const int N=12,M=(1<<9)+2;
int bit[M];
bool ban[N][N];
char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline LL Read()
{
LL now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',now%=mod,c=gc());
return now;
}
inline int FP(int x,int k)
{
int t=1;
for(; k; k>>=1,x=1ll*x*x%mod)
if(k&1) t=1ll*t*x%mod;
return t;
}
inline bool Check(int a,int b)
{
if(a<3) return b>=3;
if(a>5) return b<=5;
return b<=2||b>=6;
}
int Calc()
{
static int f[M];
memset(f,0,sizeof f);
f[0]=1;
int all=(1<<9)-1;
for(int s=0; s<all; ++s)
{
int cnt=bit[s];
if(cnt%3) continue;
for(int a=0; a<9; ++a)
if(!(s>>a&1)&&!ban[cnt+1][a+1])
for(int b=0; b<9; ++b)
if(!(s>>b&1)&&!ban[cnt+2][b+1]&&Check(a,b))
for(int c=0; c<9; ++c)
{
if(s>>c&1||ban[cnt+3][c+1]||!Check(a,c)||!Check(b,c)) continue;
int ss=s|(1<<a)|(1<<b)|(1<<c);
f[ss]+=f[s], Mod(f[ss]);
}
}
return f[all];
}
int main()
{
const int Sum=719935075;//Read(); //6670903752021072936960
const int tot=46656,inv=549081465;// int tot=Calc(),inv=FP(tot,mod-2);
for(int i=1; i<M; ++i) bit[i]=bit[i^lb(i)]+1;
for(int T=read(); T--; )
{
for(int i=1; i<=9; ++i)
{
register char c=gc(); for(;c!='0'&&c!='1';c=gc());
ban[i][1]=c=='1';
for(int j=2; j<=9; ++j) ban[i][j]=gc()=='1';
}
int now=Calc();
printf("%d
",(int)(1ll*Sum*now%mod*inv%mod));
}
return 0;
}
B 红绿灯(最短路Dijkstra)
不管一条边怎么样,我们到达一个点时肯定是越早越好啊(不会更差)。
所以直接Dijkstra就行了。边权就模拟一下。
//2762ms 54532kb
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
#define mp std::make_pair
#define pr std::pair<LL,int>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef int LL;//longlong?
const int N=5e5+6,M=2e6+7;
int Enum,H[N],nxt[M],to[M],len[M],K[M],L[M],R[M];
char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline void AE(int r,int l,int k,int d,int v,int u)
{
to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
}
inline int Calc(int now,int d,int k,int l,int r)
{
int tm=0;
if(now>r) tm+=k-now+l;
else if(now<l) tm+=l-now;
else if(r-now+1>=d) return d;
else d-=r-now+1, tm+=k-now+l;
now=(d-1)/(r-l+1), tm+=now*k, d-=now*(r-l+1);//(d-1)/len not d/len!
return tm+d;
}
void Dijkstra(int n)
{
static LL dis[N];
static bool vis[N];
static std::priority_queue<pr> q;
memset(dis,0x3f,sizeof dis);
dis[1]=0, q.push(mp(0,1));
while(!q.empty())
{
int x=q.top().second; q.pop();
if(vis[x]) continue;
vis[x]=1; LL ds=dis[x];
for(int i=H[x],v,tm; i; i=nxt[i])
if(tm=Calc(ds%K[i],len[i],K[i],L[i],R[i]),dis[v=to[i]]>ds+tm)
q.push(mp(-(dis[v]=ds+tm),v));
}
for(int i=1; i<=n; ++i) printf("%d
",dis[i]);
}
int main()
{
Enum=1; int n=read(),m=read();
for(int i=1; i<=m; ++i) AE(read(),read(),read(),read(),read(),read());
Dijkstra(n);
return 0;
}
C 轰炸(计算几何 圆并)
求圆并,然后找覆盖(k)次的部分?
好不NOIP啊,咕了。
咕
考试代码
B
迷之全RE懒得调。
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
#define Add(x,y) (x+y>=20?x+y-20:x+y)
typedef long long LL;
const int N=5e5+6,M=2e6+7;
const LL INF=0x3f3f3f3f3f3f3f3f;
int Enum,H[N],nxt[M],to[M],len[M],K[M],L[M],R[M],f[M>>1][20];
char IN[MAXIN],*SS=IN,*TT=IN;
struct Node
{
LL ds; int x,tm;
bool operator <(const Node &a)const
{
return ds>a.ds;
}
};
inline int read()
{
int now=0;register char c=gc();
for(;!isdigit(c);c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now;
}
inline void AE(int r,int l,int k,int d,int v,int u)
{
to[++Enum]=v, nxt[Enum]=H[u], H[u]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
to[++Enum]=u, nxt[Enum]=H[v], H[v]=Enum, len[Enum]=d, K[Enum]=k, L[Enum]=l, R[Enum]=r;
for(int i=0; i<k; ++i)
{
int tmp=i,tm=0,dd=d;
if(tmp>r) tm+=l+k-tmp;
else if(tmp<l) tm+=l-tmp;
else if(tmp!=l)
{
if(r-tmp+1>=dd) {f[Enum>>1][i]=dd; continue;}
else dd-=r-tmp+1, tm+=k-tmp+l;
}
tmp=dd/(r-l+1), tm+=tmp*k, dd-=tmp*(r-l+1);
f[Enum>>1][i]=tm+dd;
}
}
void Dijkstra(int n)
{
static bool vis[N][20];
static LL dis[N][20];
static std::priority_queue<Node> q;
memset(dis,0x3f,sizeof dis);
dis[1][0]=0, q.push((Node){0,1,0});
while(!q.empty())
{
Node tmp=q.top(); q.pop();
LL ds=tmp.ds; int x=tmp.x, tm=tmp.tm;
if(vis[x][tm]) continue;
vis[x][tm]=1;
for(int i=H[x],v,use,tmp; i; i=nxt[i])
{
v=to[i], use=f[i>>1][tm%K[i]], tmp=Add(tm,use);
if(dis[v][tmp]<=ds+use) continue;
q.push((Node){dis[v][tmp]=ds+use,v,tmp});
}
}
for(int i=1; i<=n; ++i)
{
LL ans=INF;
for(int j=0; j<20; ++j) ans=std::min(ans,dis[i][j]);
printf("%lld
",ans);
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
Enum=1; int n=read(),m=read();
for(int i=1; i<=m; ++i) AE(read(),read(),read(),read(),read(),read());
Dijkstra(n);
return 0;
}
C
为啥输出0.0000没分啊 明明有理有据啊
#include <cstdio>
#include <cctype>
#include <algorithm>
#define gc() getchar()
typedef double db;
const int N=105;
int n,K,Lim;
struct Point
{
int x,y,a;
}p[N];
inline int read()
{
int now=0,f=1;register char c=gc();
for(;!isdigit(c);c=='-'&&(f=-1),c=gc());
for(;isdigit(c);now=now*10+c-'0',c=gc());
return now*f;
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
for(int T=read(); T--; )
{
n=read(),K=read(),Lim=read();
for(int i=1; i<=n; ++i) p[i]=(Point){read(),read(),read()};
if(K==1||1) printf("0.0000
");
// else if(!Lim && K==n) Subtask3::Main();
// else if(!Lim) Subtask1::Main();
}
return 0;
}