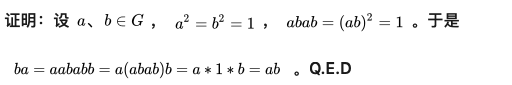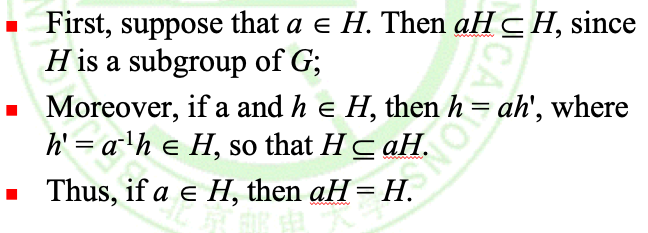10.3群，群直积，商群

群，群直积，商群

群(Groups)

如果独异点(G, *)中的每个元素均存在逆元(必定是唯一的)，那么它便升级为群

集合S + 二元运算(自带封闭性) -> ((G, *))，如果((G, *))满足结合律，那么((G, *))升级为半群 -> ((G, *))存在单位元e(必定是唯一的)，那么((G, *))升级为独异点 -> ((G, *))中每个元素存在逆元(必定是唯一的)，那么((G, *))升级为群

阿贝尔群(Abelian)

群G中任意两个元素a，b∈G，均满足阿贝尔律(交换律):ab = ba，那么群G升级为阿贝尔群

如:证明(G, *)是阿贝尔群

1. 证明*对于G是一个二元运算(证明封闭性)
2. 证明结合律
3. 找出单位元
4. 找出逆元
5. 证明交换律
   
   
   

定理1:

逆元存在必唯一(显然)

定理2:

群G具有消去律(Witt律)，包括左消去律和右消去律

定理3:

群G中满足:

• ((a^{-1})^{-1} = a.)
• ((ab)^{-1} = b^{-1}a^{-1})

定理4:

如果G是群，a，b是群G中的元素，那么:

方程(ax = b)只有G中的唯一解
方程(ya = b)只有G中的唯一解

有限群(Finte Group)

群G中元素如果是有限的，则称为有限群，其中G的元素称为G的阶(order)，记为|G|
显然，有限群能通过乘法表表示，或者说能用乘法表表示的群都是有限群

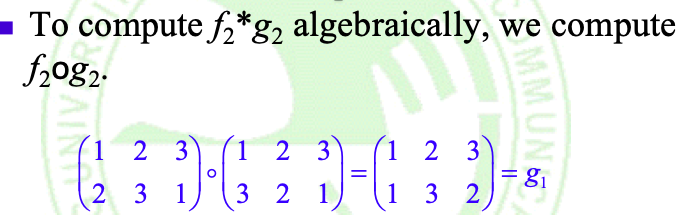
一个重要的群--n次对称群

置换:

通过轮换概念，我们可以知道置换也是群(但没必要)

对称群(symmetric group on n letters)

对称群是指含置换群为子类的一类具体的有限群

对于集合X上的双射: f: X -> X(也就是置换)

当X为有限集合时，置换的复合运算和(二元运算)部分置换操作(元素)构成了对称群，如:

下给出(S_3):

Note:n次对称群的阶为n!

子群(Subgroup)

令H是群G的一个子集，如果H满足群定义，那么H就是G的子群

(H_1 = {e}, H_2 = G)显然也是群，我们称这两个群为G的平凡子群(trivial subgroup)

G的生成群是除平凡子群外最简单的生成群(显然)

定理5:

设有群((G, *))和群((G', *')),并且有同态映射f:G -> G'，那么:

(a). 如果e是G的幺元，e'是G'的幺元，那么f(e) = e'
(b). 如果a∈G,那么(f(a^{-1}) = (f(a))^{-1})
(c). 如果H是G的子群，那么f(H) = {f(h)|h∈H}也是G'的子群

Note:同构映射(isomorphism)会保持根据二元运算定义的所有性质(可以运用此性质来反证两个群不是同构)

如群(S_3)和(Z_6)都是阶为6的群，但前者不是Abelian，而后者是，故二者不同构

克莱因四元群(Klein 4 group)

表示:Klein = {e, a, b, ab};
克莱因群的所有元素都2阶的，克莱因四元群是最小的非循环群。然而，它又是一个阿贝尔群

循环群(cyclic group)

定义:循环群。由一个元素反复运算生成的群(G = {a^n | n ∈ Z })称为循环群，简记为(<a>)，a称为这个循环群的生成元。

Note:

1. 循环群都是阿贝尔群,并且循环群的任意子群也是阿贝尔群
2. 循环群G中的任意元素都是G或G的子群A的生成元。
   
3. 群G的元素a的阶，是指由元素a生成的G的生成子群的阶，有:若群G中每一个非幺元素的阶均为2，则G是Abel群
   
4. Lagrange定理:设G为有限群，则G中每个元素g的阶均是|G|的因子;若G有子群，则任意子群A的阶都是|G|的因子。
5. p(素数)阶群G均是Abel群，并且同构于(Z_p)。
   
6. 可见，4阶群都是Abel群

群直积和商群(Products and Quotients of Groups)

定理1:群直积

由群(G_1和群G_2)的乘积得到的群是群直积，且定义为:

((a_1, b_1)(a_2, b_2) = (a_1a_2, b_1b_2))

证明和半群直积证明类似

设群(G_1和群G_2)都是mod2加法群(Z_2)(假设我们令0和1来表示等价类[0]和[1])，那么其乘积群G的乘法表如下:

如果我们通过如下定义函数，可以得到乘积群G和V/(Z_4)(唯二阶为4的群)同构:

NOTE

更一般的，我们可以得到如下:

定理2:商群

和商半群类似，通过定义在群G上的同余关系R和二元运算 口，我们能得到商半群(G/R, 口)， 其中二元运算 口 被定义为:

• [a] 口 [b] = [a*b]

只需证明其有逆元即可

推论1:

显然函数(f_R(a) = [a]:G -> G/R)是一个群同态

推论2:

同态基本定理对群是同样适用的

陪集(coset)

定义:设H是群G的一个子集，a∈G，则集合aH(Ha)称为由a所确定的H在G中的左配集(右陪集)，简称为H关于a的左陪集(右陪集)，元素a称为陪集aH（Ha）的代表元素。
如果对于任何a∈G，均有aH = Ha，那么子群H称为G的正规子群

Waring:Ha = aH并不代表对于所有的h∈H，ha=ah均成立
意思是存在h，h'∈H,使得ha = ah'

如果H是G的子群，那么如果元素a∈H，就有:aH = H

证明:

EXP(求全部元素关于子群H的左陪集):

Note:1.由这个例子，我们可以清晰的看到:对于任意a，b∈G,要么aH = bH，要么aH ∩ bH = ∅ (右陪集同理) ==》 通过子群H，我们就像同余关系一样对G中的元素进行了划分，那么我们可以以此为基础来构造商集
2.观察例子，我们能发现:任意元素x∈G,x一定∈xH,其实这是一个普适规律(可以拿来快速求陪集？)

定理3:

设R是群G上的同余关系，H = [e]显然是群G的一个子群，那么:

对于任意a∈G，均有:[a] = aH = Ha,即H是G的正规子群

通过定理3和推论1，我们可以通过正规子群N = [e]的所有陪集来进行构建商集，其中，二元运算定义为:

(aN)(bN) = [a] 口 [b] = [ab] = abN

同时有函数(f_R: G -> G/R)，定义为:

(f_R(a) = aN)

显然，(f_R)是从G到G/R的同态，我们也经常写成G/N

定理4:

设G的正规子群N，设定义在G上的关系R:

• a R b 当且仅当 (a^{-1}b)∈ N

那么有:

(a). R是G上的同余关系
(b). N是在R关系中的等价类[e]

可见，群G上的同余关系，正规子群H和G -> G/R(或G')的同态映射是等价的

推论2:

设同态映射f:G -> G'，那么f的核(kernel)，记为ker(f)，定义为:ker(f) = {a ∈ G|f(a) = e'}，那么:

1. ker(f)是G的正规子群
2. 商群G/ker(f)和G'同构

EXP:

(f: Z -> Z_n)定义为:f(m) = [r], 其中r = m%n, 那么ker(f) = nZ