题面
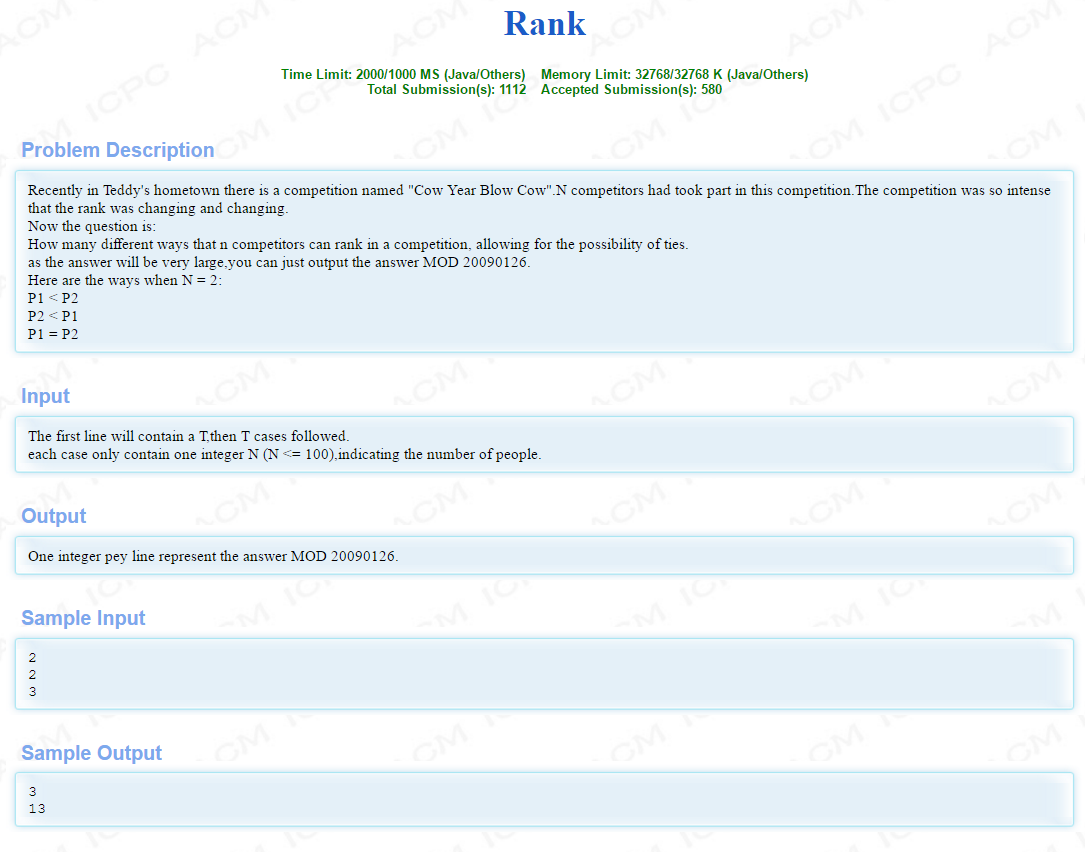
题目链接
题目大意
有 n 位选手参加比赛,每个选手有一个排名
排名可能出现并列的情况,问一共有多少种排名情况
解题思路
第二类Stirling
先把排名当做集合,排名为 1 的人数即放入集合 1 的人数
再把集合等效化,即把集合 1 和集合 2 看作是完全相同的集合
那么此时题目就可以转换为将 n 个物品放入若干个完全相同的集合的方案数
可得递推式 dp[i][j] 表示前 i 个物品用了 j 个完全相同的集合的方案数
其中 dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] * j :
①、前 i - 1 个物品构成了 j - 1 个集合,第 i 个物品构成第 j 个集合
②、前 i - 1 个物品构成了 j 个集合,则第 i 个物品可以放入 1 ~ j 个集合
那么 ans = ∑ dp[n][i]
然而这只是集合等效化后的答案,实际上当我们使用的 i 个集合应该是完全不同的
所以为了恢复等效化我们还需要乘上 i 的全排列即 i!
那么现在 ans = ∑ dp[n][i] * i!
AC_Code
#include<bits/stdc++.h> #define int long long using namespace std; const int N = 1e3 + 10 , mod = 20090126; int dp[N][N] , fac[N]; void init() { fac[0] = 1 , dp[1][1] = 1 , dp[0][0] = 1; for(int i = 1 ; i <= 100 ; i ++) { fac[i] = fac[i - 1] * i % mod; for(int j = 1 ; j <= i ; j ++) { dp[i][j] = dp[i - 1][j] * j + dp[i - 1][j - 1]; dp[i][j] %= mod; } } } signed main() { init(); int t ; cin >> t ; while(t --) { int n , ans = 0; cin >> n ; for(int i = 1 ; i <= n ; i ++) ans += dp[n][i] * fac[i] , ans %= mod; cout << ans << ' '; } return 0; }