Java数据结构和算法初探

//Data structure and algorithm

 一、数据结构和算法

 在任何语言中都是通用的,是一独立的学科,除了数据结构就是算法

 常用的数据结构:

 数组(Aray),( Stack),队列( Queue),二叉树、链表( Linked List)、哈希表、散列表(Hash)等算法

 冒泡排序( bubble sort)、选择排序( selection sort),二分法查找等

 数据结构和算法用得好,程序执行效率就高

 

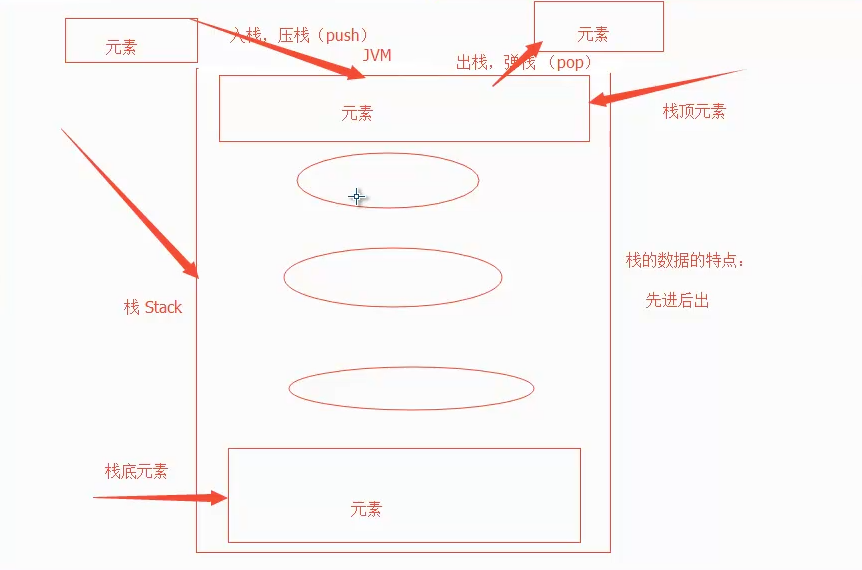
 二、Java中栈

 

栈按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在桟顶,需要读数据的时候从顶开始弹出数据(最后一个数据被第一个读出来)。

是允许在同一端进行插入和删除操作的特殊銭性表。允许进行插入和删除操作的端称为栈顶(top),另一端为钱底( botton);底固定,而栈顶浮动中元素个数为零时称为空。

插入一股称为进栈(PUSH),删除则称为退栈(POP)。栈也称为先进后出。

栈可以用来在函数调用的时侯存储断点,做递归时要用到栈!

 

三、使用图形，画出一个程序的执行流程

方法的执行原理：

方法在调用的时候，才会给该方法在内存中分配空间;如果方法只声明，不调用不会分配空间

方法调用的时候在"栈"中分配空间，（JVM内存中有一块内存是 栈内存）

方法调用其实是"压栈"，方法结束其实就是"弹栈"

只有结束符号才能"弹栈"

 

public class Algorithm {

    public static void main(String[] args) {
      int i = 100;
      m1(i);
    }

    public static void m1(int i){
        m2(i);
    }

    public static void m2(int i){
       m3(i);
    }
    public static void m3(int i){

        System.out.println("m3中的方法中的i = " + i);
    }
    //层层传递
    public static void m4(int i){
        System.out.println("m3中的方法中的i = " + i);
    }

}

四、递归

/*

 关于方法的递归调用

    1.方法的递归调用就是方法自身调用自身(自己调自己)

    2.以下程序因为递归没有结束条件，所以 一直在压栈，没有弹栈，导致栈内存溢出!

    3.所以递归必须要有结束条件

 */

 

public class Recursion {
    public static void main(String[] args){
      array(1);

    }
    public static void array(int i){
        System.out.println("Array 被弹出来了");
      array(i);
    }
    /*
    Exception in thread "main" java.lang.StackOverflowError
    at Recursion.array(Recursion.java:7)
    at Recursion.array(Recursion.java:7)
     */
}

案例一、计算1-N的求和【不使用递归，怎么做】

 

public class Recursion2 {

    public static void main(String[] agrs){
       int value = sum(6);
       System.out.println("value = " + value);
    }
    //该方法需要完成1-N的求和
    //1+2+3+...+N
    public static int sum(int n){
        int sum = 0;
        for (int i = 0; i <= n ; i ++){
            //sum =  sum + i;
            sum += i;
        }
        return sum;
    }
    //value = 21

    //递归操作
    public static int sum1(int n){
         if (n == 1){
             return 1;
         }else  {
             return  n + sum1(n-1);
         }
    }
    //value = 21

}

案例二、计算N的阶乘

public class Recursion3 {

    public static void main(String[] args){
     int n = 5;

    System.out.println("N的阶乘 = " + sum2(n));//N的阶乘 = 120
    }
    //1.不使用递归
    public static int sum(int n){
        int result = 1;
        for (int i = 1 ; i <= n ; i++){
            result = result * i;
        }
        return result;
    }
    //2.使用递归
    public static int sum2(int n ){
        if (n == 1){
            return  1;
        }else  {
            return n * sum2(n-1);
        }
    }

}