视频、图形图像处理之Opencv技术记录（六）、均衡直方图

参考资料：https://docs.opencv.org/3.4.2/d4/d1b/tutorial_histogram_equalization.html

目标

在本教程中，您将学习：

• 什么是图像直方图以及为什么它有用
• 通过使用OpenCV函数cv :: equalizeHist来均衡图像的直方图

理论

什么是图像直方图？

• 它是图像强度分布的图形表示。
• 它量化了所考虑的每个强度值的像素数。

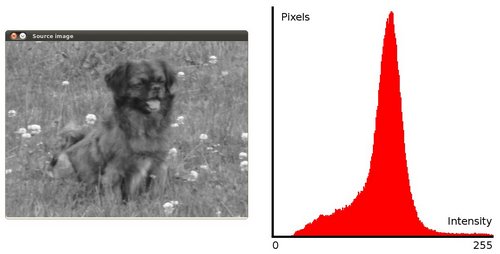
什么是直方图均衡？

• 这是一种改善图像对比度的方法，以便拉伸强度范围（另请参阅相应的维基百科条目）。
• 为了更清楚，从上面的图像中，您可以看到像素似乎聚集在可用的强度范围的中间。直方图均衡的作用是延伸此范围。请看下图：绿色圆圈表示人口密集的强度。应用均衡后，我们得到一个直方图，如中间的数字。生成的图像显示在右侧的图片中。

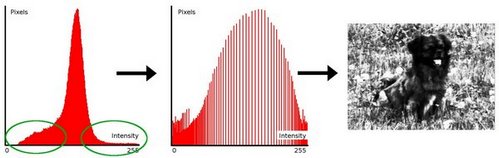
它是如何工作的？

• 均衡意味着将一个分布（给定的直方图）映射到另一个分布（更宽和更均匀的强度值分布），因此强度值分布在整个范围内。

• 要实现均衡效果，重映射应该是累积分布函数（cdf）（更多细节，请参阅学习OpenCV）。对于直方图，其累积分布是：

  

  要将其用作重新映射函数，我们必须对进行归一化，使得最大值为255（或图像强度的最大值）。从上面的例子中，累积函数是：

  

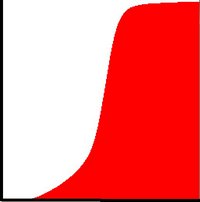
• 最后，我们使用简单的重新映射程序来获得均衡图像的强度值：

  

码 

C ++

• 这个程序做了什么？
  • 加载图像
  • 将原始图像转换为灰度
  • 使用OpenCV函数cv :: equalizeHist均衡直方图
  • 在窗口中显示源图像和均衡图像。

• 可下载的代码：点击这里
• 代码一目了然：

  #include "opencv2/imgcodecs.hpp"
  #include "opencv2/highgui.hpp"
  #include "opencv2/imgproc.hpp"
  #include <iostream>
  using namespace cv;
  using namespace std;
  int main( int argc, char** argv )
  {
      CommandLineParser parser( argc, argv, "{@input | ../data/lena.jpg | input image}" );
      Mat src = imread( parser.get<String>( "@input" ), IMREAD_COLOR );
      if( src.empty() )
      {
          cout << "Could not open or find the image!
  " << endl;
          cout << "Usage: " << argv[0] << " <Input image>" << endl;
          return -1;
      }
      cvtColor( src, src, COLOR_BGR2GRAY );
      Mat dst;
      equalizeHist( src, dst );
      imshow( "Source image", src );
      imshow( "Equalized Image", dst );
      waitKey();
      return 0;
  }

说明 

C ++

• 加载源图像：

    CommandLineParser parser( argc, argv, "{@input | ../data/lena.jpg | input image}" );
    Mat src = imread( parser.get<String>( "@input" ), IMREAD_COLOR );
    if( src.empty() )
    {
        cout << "Could not open or find the image!
" << endl;
        cout << "Usage: " << argv[0] << " <Input image>" << endl;
        return -1;
    }

• 将其转换为灰度：

cvtColor( src, src, COLOR_BGR2GRAY );

• 使用函数cv :: equalizeHist应用直方图均衡：

    Mat dst;
    equalizeHist( src, dst );

由于可以很容易地看到，唯一的参数是原始图像和输出（均衡）图像。

• 显示两个图像（原始图像和均衡图像）：

    imshow( "Source image", src );
    imshow( "Equalized Image", dst );

• 等到用户存在该程序

    waitKey();

结果

1. 为了更好地理解均衡的结果，让我们介绍一个对比度不大的图像，例如：

   

   顺便说一下，这个直方图：

   

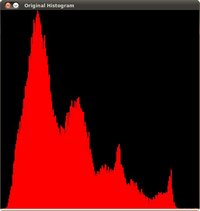
   请注意，像素聚集在直方图的中心周围。

2. 在我们的程序中应用均衡后，我们得到了这个结果：

   

   这个形象肯定有更多的对比。看看它的新直方图如下：

   

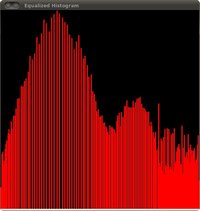
   请注意像素数在强度范围内的分布情况。