文章:Clustering Convolutional Kernels to Compress Deep Neural Networks
链接:http://openaccess.thecvf.com/content_ECCV_2018/papers/Sanghyun_Son_Clustering_Kernels_for_ECCV_2018_paper.pdf

这篇文章主要是研究模型的压缩和加速。其他的文章大多数都只研究网络结构中的冗余参数或影响不大的结构,用剪枝的方法来压缩模型。作者从另一个方面研究,将相似的卷积统一表示,极大程度压缩了所需储存内存,并与剪枝的方法不冲突(可同时使用)。
贡献:
1.提出了一种新的方法,将k-means聚类应用于2d核上,以压缩和加速cnn。这是第一个考虑内核冗余空间模式的网络压缩方法。
2.提出的变换不变聚类方法扩展了具有几何变换的核心点的有效数目。
3.实验表明,提出的的方法普遍适用于各种cnn架构和数据集。特别是,我们的压缩后的resnet在lsvrc12图像分类上比原始模型在10倍以上的压缩比上达到了更高的精确度。
一、用两个参数表示一个卷积核(压缩)
文中选择聚类的卷积核为3*3;这在大多数现有模型中出现的最多。VGG16有1,634,496 多个3×3 kernels 占了所有参数量的99.9%。ResNet-56 和DenseNet-12-40 分别有94,256 和101,160 kernels,也占了参数量的绝大部分。
聚类的为2维卷积核, 。Cout为卷积输出通道,Cin为卷积输入通道,h,w为卷积图像大小。每个卷积核的计算可以写为
。Cout为卷积输出通道,Cin为卷积输入通道,h,w为卷积图像大小。每个卷积核的计算可以写为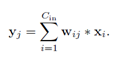 。其中i为输入通道,j为输出通道。用k-means将wij聚为k类,表达式为
。其中i为输入通道,j为输出通道。用k-means将wij聚为k类,表达式为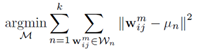 ,其中un为正常的求均值,
,其中un为正常的求均值, ,与传统的k-means没有任何区别。
,与传统的k-means没有任何区别。
由于内核权重的分布可以在不同的卷积层之间变化,我们利用卷积的基本概念,对所有的核进行归一化处理。具体地说,我们把形状相似但规范不同的内核放在一起处理,因为它们在过滤中表现出相似的行为。因此,我们使用归一化的内核,而不是直接计算内核与其原值之间的距离。K-means 聚类表达写为: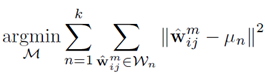 ,其中
,其中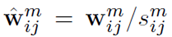 为归一化的卷积核。
为归一化的卷积核。 为放缩的比例参数。
为放缩的比例参数。 为3*3卷积核的中心元素。
为3*3卷积核的中心元素。
举个例子,对于一个卷积核wij,可以近似的用sij*ulij表示。其中s表示放缩比例,u表示其所属的聚类中心,l为所属的中心在所有聚类中心中的编号。这个时候,一个3*3的卷积核,我们可以用sij和lij两个参数近似表示。
二、一些基于共享参数的计算小技巧(加速)
正常计算卷积的式子为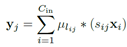 ,对于一个卷积层而言,需要计算2*w*h*Cin*Cout个乘法。
,对于一个卷积层而言,需要计算2*w*h*Cin*Cout个乘法。
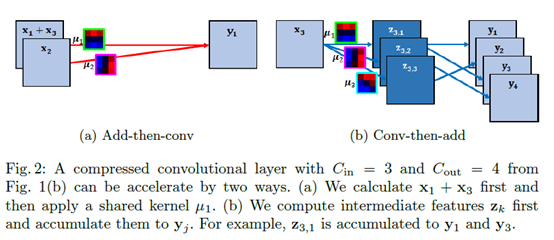
先说(a)先加再卷积,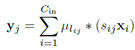

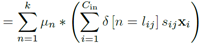 ,对于同一个输出而言,我们的聚类中心设为k个,即这里用到的卷积核不会超过k个,不妨即为v个。则对于不同的输入,如果乘以的卷积核相同,我们可以先将这些输入相加,最后再算卷积乘法。即对一个输出计算v个乘法,当然,每个输出的用到的聚类中心v可能不同,这一层卷积的乘法总数为所有输出对应的v相加。
,对于同一个输出而言,我们的聚类中心设为k个,即这里用到的卷积核不会超过k个,不妨即为v个。则对于不同的输入,如果乘以的卷积核相同,我们可以先将这些输入相加,最后再算卷积乘法。即对一个输出计算v个乘法,当然,每个输出的用到的聚类中心v可能不同,这一层卷积的乘法总数为所有输出对应的v相加。
再说(b)先卷积再相加,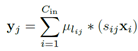
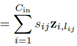 ,
,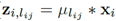 。因为是同一个输入,它的正则化系数(放缩比例)一定相同,即可以将s提出来最后乘,假设这个输入总共用到λ个聚类中心。这时对于这个输入,只需要算λ乘法。
。因为是同一个输入,它的正则化系数(放缩比例)一定相同,即可以将s提出来最后乘,假设这个输入总共用到λ个聚类中心。这时对于这个输入,只需要算λ乘法。
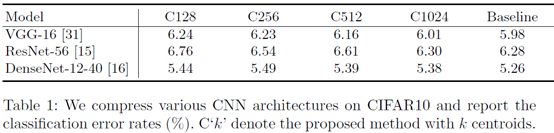
作者使用下面三个模型在CIFAR10上进行了实验,仅对3*3的卷积核进行聚类近似表示,C128代表聚类中心数目为128.分类效果没有明显下降。注:网络进行了一些小修改,例如VGG16的三个全连接变为一个。
然后分析了压缩比例和提升速度

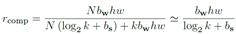 ,N为网络中3*3核的数目,bw为一个权重占内存大小(32b),h*w为图大小,k为聚类中心数目,bs为正则化参数(放缩比例)占内存大小。所以说,上式分子为传统需要内存,储存每个权重的参数。而分母则为文中优化后的占内存,前半部分为这N个核的所属聚类中心编号和放缩参数的内存,后半部分为聚类中心的内存。由于k远远小于N,近似等于。。
,N为网络中3*3核的数目,bw为一个权重占内存大小(32b),h*w为图大小,k为聚类中心数目,bs为正则化参数(放缩比例)占内存大小。所以说,上式分子为传统需要内存,储存每个权重的参数。而分母则为文中优化后的占内存,前半部分为这N个核的所属聚类中心编号和放缩参数的内存,后半部分为聚类中心的内存。由于k远远小于N,近似等于。。
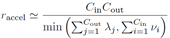 加速的话上面已经分析了加速算法(a)add-then-conv和(b)conv-then-add,v和λ就是用到的聚类中心的个数。由于这两个算法不能同时使用,所以取最小值。约等于是因为加法计算也是要时间的。
加速的话上面已经分析了加速算法(a)add-then-conv和(b)conv-then-add,v和λ就是用到的聚类中心的个数。由于这两个算法不能同时使用,所以取最小值。约等于是因为加法计算也是要时间的。
三、变换不变聚类法(TIC)
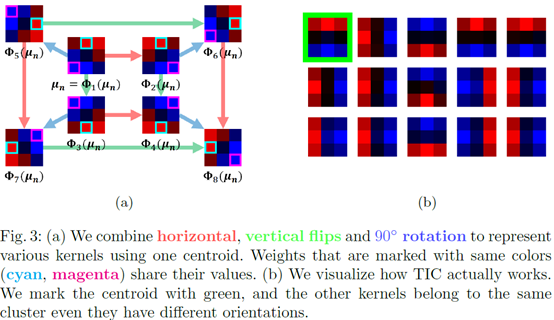
对一个聚类中心,它的水平翻转,竖直翻转,旋转90°。这八种上图做所示算作一个聚类中心。。注意:不是在原来的聚类结果上再聚一次类,而是在原有的聚类结果上进行修正,即考虑了变换的情况下,对原来的没有聚类过的数据上进行变换不变聚类。这时,聚类的表达式就变成了下面这个样子。

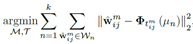
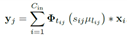
四、实验结果
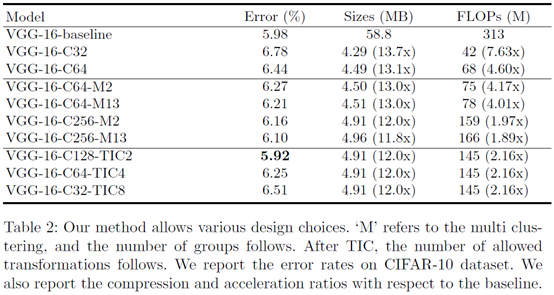
C32代表聚类中心为32,C64代表聚类中心为64。M2表示模型分为两部分,前10层共用一组聚类中心,后3层共用另一组聚类中心。M13代表13层卷积层每层都用一组聚类中心。TIC则是变换不变聚类的缩写,2,4,8分别表示只有竖直翻折,只有竖直水平翻折,翻折并旋转。注:有可能出现所有核数目没有预设的聚类中心个数多的情况,这时两者取最小。
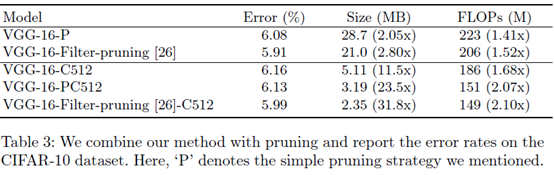
文章的方法和剪枝的方法不冲突,可以同时使用,使得压缩和计算效果更好。P代表最常见的剪枝,基于L1去除一半的卷积核。原文:P is simple thresholding which removing 50% of the spatial kernels from each layer based on their L1 norms;filter-pruning则是一篇文章(Pruning filters for efficient convnets. In: International Conference on Learning Representations (2017))提出的剪枝方法,我没去看就不解说了。
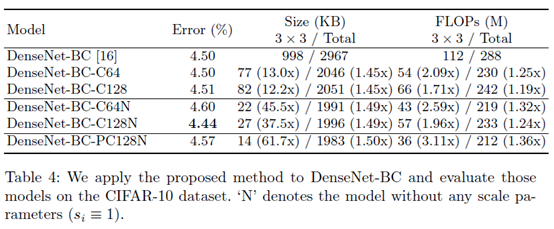
这是在最近很火的有瓶颈结构的网络上做的实验,因为1*1的卷积占了大部分,压缩的整体效果没有在VGG16上明显。但是错误率并没有明显上升,表明瓶颈对正常网络的影响在这种压缩表示中没有消失。
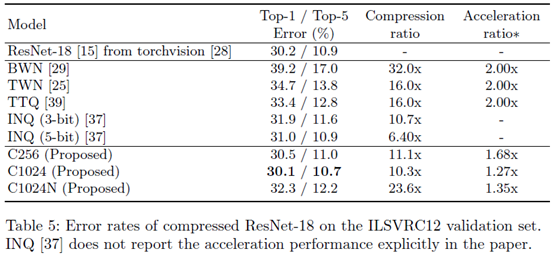
最后是对其他压缩算法的比较。由于大家的硬件软件的配置不一样,这些东西并不好比较,作者也只比较了一部分。
五、其他:
这篇文章和大多数压缩的想法不太一样,用了索引和聚类的方式近似的表示出所有需要储存的参数来进行压缩。和大多数文章中采用的去除冗余的卷积结构的做法可以同时使用。但是文章只描述了3*3的卷积,提到了对7*7卷积做了相似的事情。但是对1*1卷积暂时没有好的处理方式。