美元对人民币汇率的大数据分析与预测

一、实验说明

文献参考：http://www.dataguru.cn/article-11339-1.html（lstm详细介绍）

https://blog.csdn.net/u011974639/article/details/77856388#?tdsourcetag=s_pcqq_aiomsg（TensorFlow及lstm代码参考）

附：本文数据不便放出，需要做实验可以自己在excel中编辑数据，数据在“二、开发准备”中有样本参考。

1.1实验内容

通过现有的数据，建立数学模型，预测出未来一个月的汇率变化趋势。本文采用美元对人民币的汇率数据，时间是1990年1月1日到2018月8月21日。利用Tensorflow搭建模型并完成预测，数学模型用Lstm（长短期记忆）人工神经网络，Lstm是RNN（循环神经网络）的一种变形，是在RNN的基础上施加了若干个门来控制，使其在长时间步的传递过程中减少信息失效的可能。

1.2实验知识点

1.2.1本次实验中将学习和实践以下知识点：

1. Python基本知识
2. Python基础库如numpy，panda，matplotlib
3. TensorFlow模块的使用
4. Lstm神经网络

1.2.2Lstm神经网络

要理解Lstm，首先需要了解循环神经网络（RNN），循环神经网络可以将信息持久化。

 

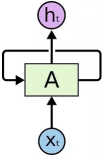
这个相对于原始的神经网络，就是加了一个环，也就是X是输入，h为输出，A为隐藏层，如果将环展开：

 

循环神经网络的一个核心思想是将以前的信息连接到当前的任务中来，但是，如果前面的信息与当前信息距离增大，RNN对于连接这些信息显得无能为力。而Lstm是一种特殊的RNN，能学习长期依赖关系。一般的RNN，其模块非常简单，只有一个tanh层。

 

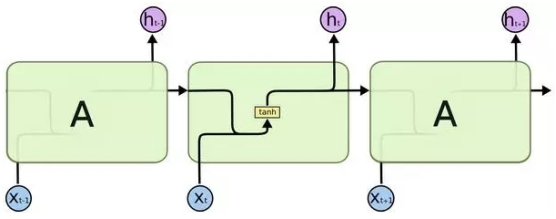
Lstm也是这种结构，但其模块的结构不同，如下所示。

 

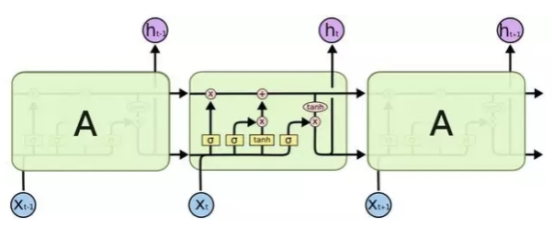
Lstm的核心是元胞状态，Lstm通过门的结构来控制元胞状态添加或者删除信息，门是一种选择性让信息通过的方法，也就是Lstm不同于RNN的地方。Lstm也有多种版本，但核心部分都是一样的，本文中不再详细展开讨论Lstm的每个部分。

1.3实验环境

1. 运行环境window7
2. 开发环境python3.6
3. 调试环境jupyter notebook

1.4适合人群

1. 具有python基础知识、神经网络基础知识
2. TensorFlow学习
3. Lstm神经网络学习

二、开发准备

安装Anaconda，Anaconda包含有非常齐全的基础库，因此非常便于使用，并且安装非常简单，只要下载解压，按照提示直接安装完毕即可。安装完成可以查看python是否可用以及python的版本。命令行输入python即可。

 

输入pip list查看库列表，部分截图如下

 

通过查看可以发现还需要安装TensorFlow库

 

实验所需文件部分数据如下所示

 

三、项目文件结构

 

四、实验内容及步骤

4.1导入实验所需要的库

import numpy as np

import tensorflow as tf

from tensorflow.contrib import rnn

import matplotlib.pyplot as plt

from tensorflow.contrib.learn.python.learn.estimators.estimator import SKCompat

from matplotlib import style

import pandas as pd

4.2数据预处理

导入数据并查看前五行数据

data = pd.read_excel('美元-人民币.xlsx',header = 0, sheetname='Sheet1')

data.head()

 

获取时间及收盘价，这里收盘价可以用其他价格替换，本文预测收盘价。

time = data.iloc[:,0].tolist()

data = data.iloc[:,4].tolist()

观察原数据基本特征。

style.use('ggplot')

plt.figure(figsize=(16,9))

plt.rcParams['font.sans-serif'] = 'SimHei' ##设置字体为SimHei显示中文

plt.rcParams['axes.unicode_minus'] = False ##设置正常显示符号

plt.title('原始数据')

plt.plot(time,data)

plt.show()

 

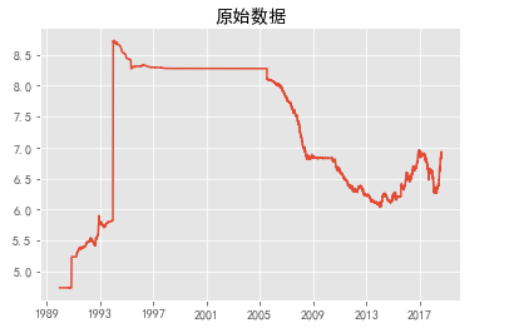
从图中可以知道原始数据值在4到9的范围，连续数据值的预测需要输出为tanh的输出，即RNN最终经由tanh激活后输出的值位于[-1,1]内，因此需要将原始数据进行缩放，方法主要有两种，极差规格化和标准化。在这里先定义缩放的函数，本文使用标准化。

def data_processing(raw_data,scale=True):

    if scale == True:

        return (raw_data-np.mean(raw_data))/np.std(raw_data)#标准化

    else:

        return (raw_data-np.min(raw_data))/(np.max(raw_data)-np.min(raw_data))#极差规格化

4.3设置基本参数

设置隐层层数，因为数据集较简单，设置一层即可，神经元个数设为32，时间步设为12，训练轮数设为2000，训练批尺寸也就是每一轮抽取的样本数量为64。

'''设置隐层神经元个数'''

HIDDEN_SIZE = 32

'''设置隐层层数'''

NUM_LAYERS = 1

'''设置一个时间步中折叠的递归步数'''

TIMESTEPS = 12

'''设置训练轮数'''

TRAINING_STEPS = 2000

'''设置训练批尺寸'''

BATCH_SIZE = 64

4.4样本生成函数

为了将原始的单变量时序数据处理成lstm可以接受的数据类型（有x输入和有y标签），需要将原始数据做进一步处理，将原始数据从第一个开始，依次采样长度为12的连续序列作为x输入，第13个数据作为y标签。

def generate_data(seq):

    X = []#初始化输入序列X

    Y= []#初始化输出序列Y

    '''生成连贯的时间序列类型样本集，每一个X内的一行对应指定步长的输入序列，Y内的每一行对应比X滞后一期的目标数值'''

    for i in range(len(seq) - TIMESTEPS - 1):

        X.append([seq[i:i + TIMESTEPS]])#从输入序列第一期出发，等步长连续不间断采样

        Y.append([seq[i + TIMESTEPS]])#对应每个X序列的滞后一期序列值

    return np.array(X, dtype=np.float32), np.array(Y, dtype=np.float32)

4.5构建lstm模型主体

'''定义LSTM cell组件，该组件将在训练过程中被不断更新参数'''

def LstmCell():

    lstm_cell = rnn.BasicLSTMCell(HIDDEN_SIZE, state_is_tuple=True)#

    return lstm_cell

'''定义LSTM模型'''

def lstm_model(X, y):

    '''以前面定义的LSTM cell为基础定义多层堆叠的LSTM，这里只有1层'''

    cell = rnn.MultiRNNCell([LstmCell() for _ in range(NUM_LAYERS)])

    '''将已经堆叠起的LSTM单元转化成动态的可在训练过程中更新的LSTM单元'''

    output, _ = tf.nn.dynamic_rnn(cell, X, dtype=tf.float32)

    '''根据预定义的每层神经元个数来生成隐层每个单元'''

    output = tf.reshape(output, [-1, HIDDEN_SIZE])

    '''通过无激活函数的全连接层计算线性回归，并将数据压缩成一维数组结构'''

    predictions = tf.contrib.layers.fully_connected(output, 1, None)

    '''统一预测值与真实值的形状'''

    labels = tf.reshape(y, [-1])

    predictions = tf.reshape(predictions, [-1])

    '''定义损失函数，这里为正常的均方误差'''

    loss = tf.losses.mean_squared_error(predictions, labels)

    '''定义优化器各参数'''

    train_op = tf.contrib.layers.optimize_loss(loss,tf.contrib.framework.get_global_step(),

                                      optimizer='Adagrad',learning_rate=0.6)

    '''返回预测值、损失函数及优化器'''

    return predictions, loss, train_op

'''载入tf中仿sklearn训练方式的模块'''

learn = tf.contrib.learn

五、实验数据记录和处理

5.1模型保存

'''初始化LSTM模型，并保存到工作目录下以方便进行增量学习'''

regressor = SKCompat(learn.Estimator(model_fn=lstm_model, model_dir='Models/model_1'))

5.2数据处理

调用前面定义好的缩放函数处理原始数据，这里先用7000个数据作为训练样本，这7000个训练数据做处理将得到6989个数据，因为每12步取一组x，第13步取为y，假设希望剩余的447个数据在测试时都预测出来，则我们需要取第6989个数据到最后一个数据，用来转换为测试样本。

'''对原数据进行尺度缩放'''

data = data_processing(data)

'''将7000个数据来作为训练样本'''

train_X, train_y = generate_data(data[0:7000])

'''将剩余数据作为测试样本'''

test_X, test_y = generate_data(data[6989:-1])

5.3训练数据

以仿sklearn的形式训练模型，这里指定了训练批尺寸和训练轮数。

regressor.fit(train_X, train_y, batch_size=BATCH_SIZE, steps=TRAINING_STEPS)

训练结果如下：

 

六、实验结果与分析

6.1预测测试样本

用训练好的模型来计算处理过的测试集，可以得到对应预测值，预测出来的数据为标准化之后的，并非原始数据，画出对比图如下。

'''利用已训练好的LSTM模型，来生成对应测试集的所有预测值'''

predicted = np.array([pred for pred in regressor.predict(test_X)])

'''绘制反标准化之前的真实值与预测值对比图'''

plt.plot(predicted, label='预测值')

plt.plot(test_y, label='真实值')

plt.title('反标准化之前')

plt.legend()

plt.show()

 

为了能看到真实数值，再定义一个反标准化函数。

'''自定义反标准化函数'''

def scale_inv(raw_data,scale=True):

    '''读入原始数据并转为list'''

    data = pd.read_excel('美元-人民币.xlsx',header = 0, sheetname='Sheet1')

    data = data.iloc[:, 4].tolist()

    if scale == True:

        return raw_data*np.std(data)+np.mean(data)

    else:

        return raw_data*(np.max(data)-np.min(data))+np.min(data)

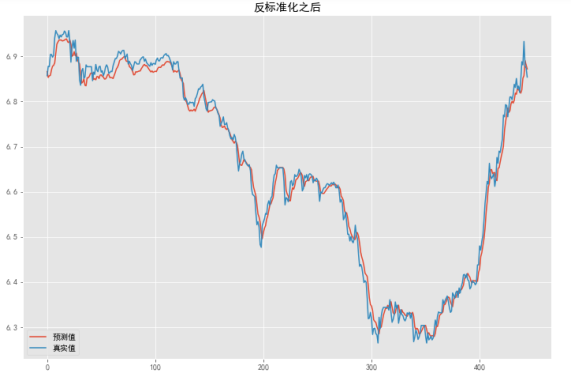
调用反标准化函数即可得到原始值，并画图观察。

sp = scale_inv(predicted)

sy = scale_inv(test_y)

'''绘制反标准化之后的真实值与预测值对比图'''

plt.figure(figsize=(12,8))

plt.plot(sp, label='预测值')

plt.plot(sy, label='真实值')

plt.title('反标准化之后')

plt.legend()

plt.show()

将预测值与前面的值连起来画图，并与原始图做对比。

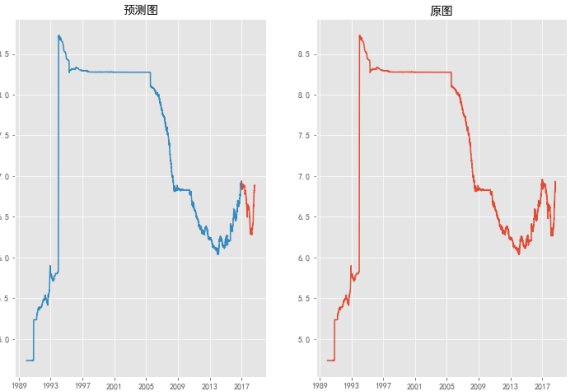
p = plt.figure(figsize=(16,9))

ax = p.add_subplot(1,2,1)

plt.plot(time[7001:-1],sp)

plt.plot(time[0:7000],scale_inv(data[0:7000]))

plt.title('预测图')

ax = p.add_subplot(1,2,2)

plt.plot(time,scale_inv(data))

plt.title('原图')

plt.show()

 

6.3计算准确率

设预测数据与原数据误差小于0.05，则算准确，由此可以按照下面方式得到准确率。

acc_num = 0

for i in range(len(sy)):

    if (abs(sp[i]-st[i])) < 0.05:

        acc_num += 1

print('准确率为：',acc_num/len(sp))

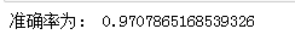
6.3预测未来20天的值

按照前面的思路，可以使用12个数据预测后一天的值，如果需要预测20天的值，可以用前面已知的12天数据预测下一天的值，这个值又放入数据中作为已知值来继续预测下一天的值，打印出预测结果。

day=20

l=len(data)

for i in range(day):

    P=[]

    P.append([data[l-TIMESTEPS-1+i:l-1+i]])

    P=np.array(P, dtype=np.float32)

    pre=regressor.predict(P)

    data=np.append(data,pre)

pre=data[len(data)-day:len(data)+1]

print(pre)

 

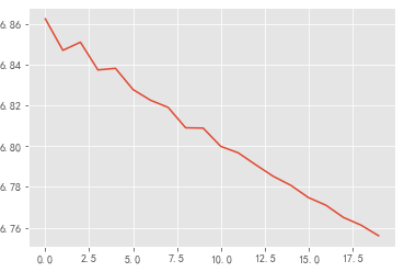
同样这个值是标准化的值，可以打印出反标准化的值和画出预测图。

#反标准化的值

print(scale_inv(pre))

#预测图

p = plt.figure()

plt.plot(scale_inv(pre))

plt.show()

 

七、问题与讨论

7.1分析结果

用训练好的模型，应用在测试集时，得到的预测结果还是令人满意的，预测出的数据误差都是小于0.1的，在0.05的误差范围内，准确率也达到97%。

对于预测未来20天的值，从预测图可以看到，数值呈下降的趋势且下降幅度较快，预测的结果其实是不准确的，原因也比较明显，在前面的测试集中，虽然是预测447个数据，但是每一次的预测都是用已知的真实值来计算的，也就是说，预测出来的值并不会加入模型中继续训练，也不会用预测出来的值作为输入参数。这预测的447个需要预测的值，本身已经在输入中了。

预测未来20天值，第一个还算是比较准确的，按照前面的做过的测试，准确率应该是达到百分九十七的，后面的数据预测时，输入是用预测出来的数据补充的，所以可能会不太准确。

7.2不足与改进

1、预测未来多天的值不准确

关于这个，可以尝试测试的时候采用预测的方法来测试，也就是输入的值用预测的值来补充，并看测试的准确率，显然这个不是很合理。另一个方法是可以在生成样本时候，y标签不要设置为1个数值，可以设置y为滞后5天或10天或其他的数据。这样预测时，即可以直接预测未来x天的数据。

2、单变量输入

在本文中，只取收盘价作为输入，在实际中，也是不合理的，因为影响汇率的因素有很多，可以尝试加入其他变量，预测结果可能会更好。