POJ 2365 Rope

题目链接：

http://poj.org/problem?id=2365

Description

Plotters have barberically hammered N nails into an innocent plane shape, so that one can see now only heads. Moreover, pursuing their mean object, they have hammered all the nails into the vertices of a convex polygon. After that they...it is awful... have roped off the nails, so that the shape felt upset (the rope was very thin). They've done it as it is shown in the figure. 
 
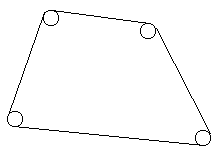
Your task is to find out a length of the rope.

Input

There two numbers in the first line of the standard input: N — a number of nails (1 <= N <= 100), and a real number R — a radius of heads of nails. All the heads have the same radius. Further there are N lines, each of them contains a pair of real coordinates (separated by a space) of centers of nails. An absolute value of the coordinates doesn't exceed 100. The nails are described in a clockwise order starting from an arbitrary nail. Heads of different nails don't adjoin.

Output

The standard output should contain in its only line a real number with two digits precision (after a decimal point) — a length of the rope.

Sample Input

4 1
0.0 0.0
2.0 0.0
2.0 2.0
0.0 2.0

Sample Output

14.28

 Hint:

题意：

给你几个顶点，给你一个圆的半径，要求你求一下以这几个点围成的多边形的周长。

题解：

简单题，简单的数学问题。

代码：

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm> 
using namespace std;
#define pi 4.0*atan(1.0)
const int maxn = 100+10;
double x[maxn],y[maxn];
double dis(double x1,double y1,double x2,double y2)
{
    return sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
}
int main()
{
    int n;
    double r;
    scanf("%d%lf",&n,&r);
    for(int i=0;i<n;i++)
        scanf("%lf%lf",&x[i],&y[i]);
    double sum=0;
    for(int i=1;i<n;i++)
        sum+=dis(x[i-1],y[i-1],x[i],y[i]);
    sum+=dis(x[0],y[0],x[n-1],y[n-1]);
    sum+=2*pi*r;
    printf("%.2lf
",sum);
}