树上差分,顾名思义,就是在树上进行差分,以起到优化复杂度的目的。主要作用是对树上的路径进行修改和查询操作,在修改多、查询少的情况下复杂度比较优秀。实际上,树上差分能够实现的操作,用线段树、树剖、$LCT$等等也可以实现,但它的优势在于实现简单,可以避免在考场上出现写题五分钟、调试两小时的情况 当然大佬可以忽略这点
差分
在讲解树上差分之前,先讲一下差分的思想。
差分,可以当做前缀和的逆运算。既然是逆运算,运算方法自然就是相反的了。定义差分数组$diff$,则运算法则为:(设原数列为$a$)
$$diff_i=a_i-a_{i-1}$$
作个比较:
| 原数列 | 9 | 4 | 7 | 5 | 9 |
|---|---|---|---|---|---|
| 前缀和 | 9 | 13 | 20 | 25 | 34 |
| 差分数组 | 9 | -5 | 3 | -2 | 4 |
| 前缀和的差分数组 | 9 | 4 | 7 | 5 | 9 |
| 差分数组的前缀和 | 9 | 4 | 7 | 5 | 9 |
显然,原数列的前缀和的差分数组还是原数列,原数列的差分数组的前缀和也是原数列,这就是差分被称为前缀和的逆运算的原因,也是差分可以用来优化操作的原因。实际上,差分优化和前缀和优化原理类似,只是实现相反。前缀和优化常常对前缀和数组作差,差分优化也常常对差分数组求前缀和。
这样,差分的概念就很清晰了。接下来开始进入正题。
树上差分
树上差分有什么作用?举个例子,如果题目要求对树上的一段路径进行操作,并询问某个点或某条边被经过的次数,树上差分就可以派上用场了。这就是树上差分的基本操作。
树上差分,就是利用差分的性质,对路径上的重要节点进行修改(而不是暴力全改),作为其差分数组的值,最后在求值时,利用$dfs$遍历求出差分数组的前缀和,就可以达到降低复杂度的目的。
树上差分时需要求$LCA$,不会的可以点击食用。
点差分
设将两点$u,v$之间路径上的所有点权增加$x$,$o=LCA(u,v)$,$o$的父亲节点为$p$,则操作如下:
diff[u]+=x,diff[v]+=x,diff[o]-=x,diff[p]-=x;
怎么样,是不是很简单!原理也很简单,举个例子:
设原树如下,现要将$2,3$之间路径上的所有点的权值增加$3$,设原权值均为$0$。
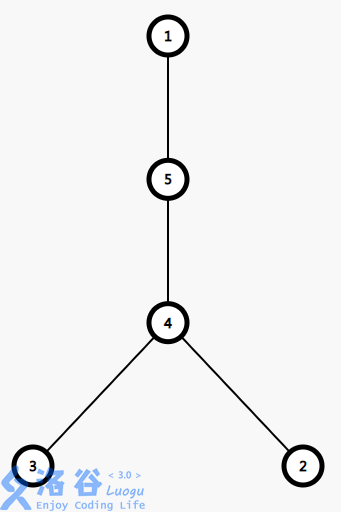
则操作后有:
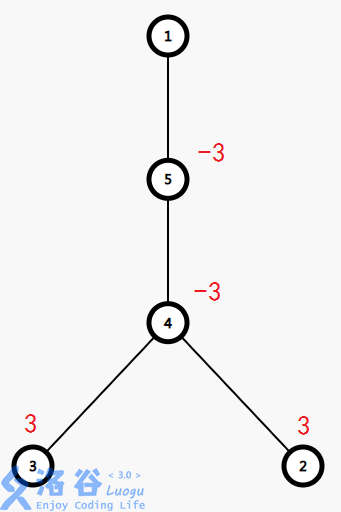
这样,只要$dfs$一遍,遍历时统计以每个节点为根的树的节点的权值和,就是当前节点的最终权值! 是不是很厉害
就是差分的思想,这里就不多说了。
边差分
思想一样,讲一下操作。
设将两点$u,v$之间路径上的所有边权增加$x$,$o=LCA(u,v)$,以每条边两端深度较大的节点存储该边的差分数组,则操作如下:
diff[u]+=x,diff[v]+=x,diff[o]-=2*x;
再举个例子,还是上面那个图 绝对不是我懒
则操作后有:
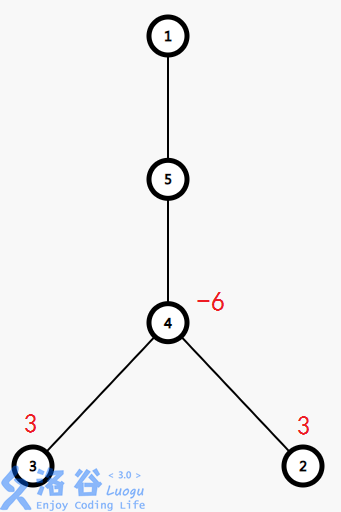
同样地,只要$dfs$一遍,遍历时统计以每个节点为根的树的节点的权值和,就是当前节点到父亲节点的边的最终权值了!
是不是很厉害
至于为什么点差分和边差分的操作不一样,很简单,请读者自己思考。
树上差分主要还是学习思想吧!
习题:
差分
综合应用题:P1083
树上差分
简单模板题:P3128
综合应用题:P2680
参考资料:
2019.7.16 于厦门外国语学校石狮分校