ST算法是求解RMQ问题的好方法,可以在0(NlogN)的预处理后实现O(1)的查询。该算法是在倍增的思想基础上实现的,比较基础,理解起来也不难。
补充几个要点:
- RMQ问题:即区间最值问题,给出一个序列a,要求求出区间[l,r]内的最大值。
- 倍增:(来自lyd的蓝书)

- log2(x)函数:返回$log_2x$,效率较高,需调用cmath库。
- 左移运算符(<<):a<<b表示$a*2^b$,效率较高,比乘法运算快。
为了实现O(1)的查询,要先预处理出每个区间的最大值。按照倍增的思想,选取2的非负整数次幂作为区间的边界,然后通过这些区间进行最值的计算。因此不妨用$f_{i,j}$表示区间[i,i+$2^j$-1]的最大值。这样就很明显了,算法过程用递推来实现。
预处理:
显然,区间[i,i+$2^{j-1}$-1]和[i+$2^{j-1}$,i+$2^j$-1]一定覆盖了区间[i,i+$2^j$-1],如下图: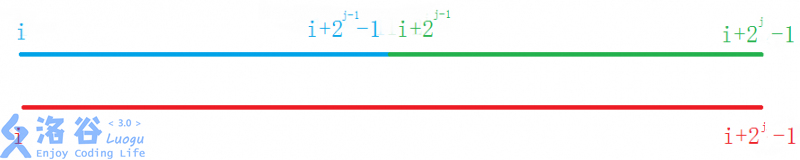
因此,区间[i,i+$2^j$-1]内的最大值就是区间[i,i+$2^{j-1}$-1]和[i+$2^{j-1}$,i+$2^j$-1]内的最大值中更大的一个。可以得出递推式:
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
显然,递推边界为$f_{i,0}==a_i$,这个很容易证明。
在预处理的循环过程中,要注意循环边界,以免越界。
预处理代码:
void pre()
{
int t=log2(n);
for(int j=1;j<=t;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
查询:
先计算出一个满足$2^t<r-l+1<2^{t+1}$的t值,即小于区间长度的2的最高次幂。
显然,区间[l,l+$2^{t}$-1]和[r-$2^t$+1,r]一定覆盖了区间[l,r],如下图:
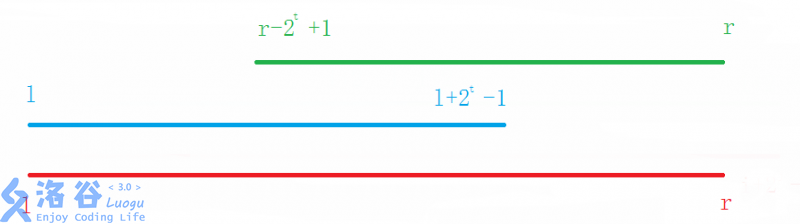
这个很好证明:因为两个子区间长度均为$2^t$,而区间[l,r]长度小于等于$2^{t+1}$,即$2*2^t$,所以区间[l,l+$2^{t}$-1]和[r-$2^t$+1,r]一定覆盖了区间[l,r]。
因此,区间[l,r]内的最大值就是区间[r-$2^t$+1,r]和[l,l+$2^{t}$-1]内的最大值中更大的一个。可以得出递推式:
ans[l][r]=max(f[l][t],f[r-(1<<t)+1][t]);
在代码实现过程中,可以不定义ans数组,直接输出答案即可。
查询代码:
int calm(int l,int r)
{
int t=log2(r-l+1);
return max(f[l][t],f[r-(1<<t)+1][t]);
}
关于f数组的大小,从上面的讲解中应该很好推出:设序列长度为N,则定义f[N][$log_2N$]。数组的大小应该在这个基础上稍大一些,防止出现一些玄学问题。
完整代码:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int N=2e5;
int cn,quel,quer,n,m,f[N][20];
void pre()
{
int t=log2(n);
for(int j=1;j<=t;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}//预处理
int calm(int l,int r)
{
int t=log2(r-l+1);
return max(f[l][t],f[r-(1<<t)+1][t]);
}//查询
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
scanf("%d",&cn);
f[i][0]=cn;
}//输入
pre();
while(m--)
{
scanf("%d%d",&quel,&quer);
printf("%d
",calm(quel,quer));
}//在线查询并输出
return 0;
}
习题:
2019.4.6 于厦门外国语学校石狮分校