目录
题目完成进度
树链剖分通常用于解决一类维护静态树上路径信息的问题,例如,给定一棵点带权的树,接下来每次操作会修改某条路径上所有点的权值(修改为同一个值或是同加上一个值等),以及询问某条路径上所有点的权值和。
当这棵树是一条链时,这个问题实际上就是一个序列上区间修改、区间询问的问题,可以用线段树等数据结构解决。
而对于其他情况,由于树的形态是不变的,因此树链剖分的策略是将这些点按照某种方式组织起来,剖分成若干条链,每条链就相当于一个序列。这样,操作的路径可以拆分为某几条链,也就是若干个完整序列或是某个序列上的一段区间,此时可以利用线段树等处理序列上区间操作的数据结构解决问题。
树链剖分的核心是如何恰当地将树剖分为若干条链。当链的划分方式确定后,我们只要将它们看做是一个个序列,将所有序列按顺序拼接起来,每条链就成为了一段区间,而序列上的区间问题是我们所熟悉和擅长解决的(并没有擅长QAQ)
下面以点带权的树为例,结合路径权值修改、路径询问权值和等问题,介绍常用的剖分方法——重链剖分
我们将树中的边分为两种:轻边和重边。下图中加粗的为重边,其余为轻边
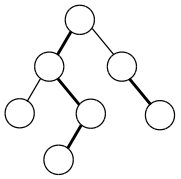
接下来我就详细讲讲究竟如何把一棵树剖分成链QWQ
1.从根结点出发(如果是无根树就任意指定一点为根),记size[u]为以结点u为跟的子树的结点个数(包括u本身)
2.找到u的所有儿子中size值最大的一个结点记为v,则(u,v)为重边,v称为u的重儿子,u到其他儿子的边为轻边。如果存在儿子结点的size值相等的情况,则随便选一个size值最大的儿子为重儿子即可
懂了吗?
这里补充几个轻重边的性质
1.如果(u,v)为轻边,则size[v]≤size[u]/2
证明:反证法。
设size[v]>size[u]/2,则size[v]必定比其他儿子的size值要大,即v一定为u的重儿子且(u,v)为重边,这与前提条件(u,v)为轻边不符
2.从根到某一结点v的路径上的轻边个数不多于log2n(n为整棵树的总结点个数)
证明:v为叶子结点时轻边数量最多。
而由上一个性质可知,每经过一条轻边,子树的结点个数至少比原来少一半,所以至多经过log2n条轻边就到达叶子节点
3.我们称某条路径为重路径(重链),当且仅当它全部由重边组成(特殊的,一个点也算一条重路径)。那么对于每个点到根结点的路径上都有不超过log2n条轻边和log2n条重路径
证明:显然每条重路径的起点和终点都是由轻边构成,而由上一个性质可知,每个点到根结点的轻边个数最多为log2n,所以重路径数量也最多为log2n
同时我们也容易发现,一个点在且只在一条重路径上,而且每条重路径一定是一条从根结点方向向叶子结点方向延伸的深度递增的路径(因为一个非叶子结点有且只有一个重儿子)
那么具体要怎么实现剖分的操作呢?
轻、重边剖分的过程可以用两次dfs实现,有时为了防止递归过深而导致栈溢出,也可以用bfs实现
剖分过程中要计算以下7个值
1.fa[x]:x在树中的父亲
2.dep[x]:x在树中的深度
3.size[x]:x的子树结点数(包括它自己)
4.son[x]:x的重儿子,即(x,son[x])为重边
5.top[x]:x所在重路径的顶部结点(深度最小)
6.seg[x]:x在线段树中的位置(下标)
7.rev[x]:线段树中第x个位置对应的树中结点编号,即seg[rev[x]]=x
第一遍dfs时可以计算出前4个值,第二遍dfs时可以计算出后3个值
而计算seg时,同一条重路径上的点需要按顺序排在连续的一段位置,也就是一段区间
maya这里我不太懂,回头再来看看吧QAQ
好了现在剖分完了,我们就要开始执行操作了QwQ
假设我们要处理路径(u,v),我们可以分别处理u,v两个点到其LCA的路径。根据性质3,路径最多可以被分解成log2n条的轻边和log2n条的重路径,那么现在我们只考虑如何维护这两种对象,即如何维护重路径和轻边
1.对于重路径,它们此时相当于一个序列,因此我们只需要用线段树来维护
2.对于轻边,我们可以直接跳过,访问下一条重路径,因为轻边的端点一定在某两条重路径上
这两种操作的时间复杂度分别为O(log2n)和O(logn),因此总复杂度为O(log2n)
将一条路径(u,v)拆分为若干条重路径的过程,实际上就是一个寻找LCA的过程
在这里我们不需要暴力的做法,因为我们已经完成了树链剖分,可以直接利用树链剖分求出LCA。
1.假定现在top[u]≠top[v],那么它们LCA可能在其中一条的重路径上,也可能在其他的重路径上,因为LCA显然不可能在top深度较大的那条重路径上,所以我们先处理top深度较大的结点。首先我们找出u,v中top深度较大的结点,假设是u,则可以直接跳到fa[top[u]]处,且跳过的这一段,在线段树中是一段区间,若我们按照深度从小到大来存储这些结点,这段区间为[seg[top[u]],seg[u]]。
2.当top[u]=top[v]时,说明他们走到了同一条重路径上,这时他们之间的路径也是序列上的一段区间,且此时u,v中深度较小的那个结点是原路径的LCA
这样我们就可以将给出的任意路径拆分成若干条重路径,也就是若干个区间,并用线段树等数据结构处理操作QWQ
呐先放一个模板的链接在这里啦^_^
1.预处理剖分
void dfs1(int u,int f){ int e,v; size[u]=1; fa[u]=f; dep[u]=dep[f]+1; for(e=first[u];e;e=next[e]){//链式前向星存边 v=go[e]; if(v!=f){ dfs1(v,u); size[u]+=size[v];//计算size if(size[v]>size[son[u]]) son[u]=v;//求重儿子 } } return; } void dfs2(int u,int f){ int e,v; if(son[u]){//先走重儿子,使重路径在线段树中的位置连续 seg[son[u]]=++seg[0];//seg存储在线段树中的下标 top[son[u]]=top[u];//如果(u,v)为重边,那么u和v在同一条重路径上 rev[seg[0]]=son[u]; dfs2(son[u],u); } for(e=first[u];e;e=next[e]){ v=go[e]; if(!top[v]){//若v是没有遍历过的点,即不是u的重儿子或父亲 seg[v]=++seg[0];//计算下标,即在线段树中继续往后加 rev[seg[0]]=v; top[v]=v;//因为不是重儿子,所以自己是重链的端点 dfs2(v,u); } } }
2.构建线段树
void build(int k,int l,int r){//k为编号,l、r分别为左右界 int mid=(l+r)>>1; if(l==r){ Max[k]=sum[k]=num[rev[l]]; //Max记录区间最大,sum记录区间和,num记录原树上结点的权值 return; } build(k<<1,l,mid); build((k<<1)+1,mid+1,r); sum[k]=sum[k<<1]+sum[(k<<1)+1]; Max[k]=max(Max[k<<1],Max[(k<<1)+1]); return; }
3.查询(u,v)路径信息
void down(int k,int l,int r){ sum[k]+=tag[k]*(r-l+1); Max[k]+=tag[k]; tag[k<<1]=tag[(k<<1)+1]=tag[k]; tag[k]=0; return; } void query(int k,int l,int r,int L,int R){//区间询问 //k为编号,l、r为线段树上这一段的左右界,L、R为询问区间的左右界 if(L>r||R<l) return; if(L<=l&&r<=R){ if(tag[k]) down(k,l,r);//标记下放 Summ+=sum[k];//Summ记录总和 Maxx=max(Maxx,Max[k]);//Maxx记录最大值 return; } int mid=(l+r)>>1,res=0; if(mid>=L) query(k<<1,l,mid,L,R); if(mid<R) query((k<<1)+1,mid+1,r,L,R); return; } void ask(int u,int v){//路径询问 int fu=top[u],fv=top[v]; while(fu!=fv){ if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv);//选择深度较大的往上跳 query(1,1,seg[0],seg[fu],seg[u]); u=fa[fu],fu=top[x];//继续往上条 } if(dep[u]>dep[v]) swap(u,v);//此时已在同一条重链上,深度较小的为LCA query(1,1,seg[0],seg[u],seg[v]); return; }
4.修改(u,v)路径信息
void Change(int k,int l,int r,int L,int R,int Val){ if(L>r||R<l) return; if(L<=l&&r<=R){ sum[k]+=Val*(l-r+1); Max[k]+=Val; tag[k<<1]=tag[(k<<1)+1]=Val;//打标记 return; } int mid=(l+r)>>1,res=0; if(mid>=L) Change(k<<1,l,mid,L,R); if(mid<R) Change((k<<1)+1,mid+1,r,L,R); return; } void change(u,v,Val){//路径修改基本跟查询相同 int fu=top[u],fv=top[v]; while(fu!=fv){ if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); query(1,1,seg[0],seg[fu],seg[u]); u=fa[fu],fu=top[x]; } if(dep[u]>dep[v]) swap(u,v); Change(1,1,seg[0],seg[u],seg[v],Val); return; }
5.单点修改信息
void change_point(int k,int l,int r,int Val,int pos){ //k为编号,l、r为线段树左右界,pos需要修改的点的位置 if(pos>r||pos<l) return; if(l==r&&r==pos){ sum[k]=Val;//Val为需要修改而成的值 Max[k]=Val; return; } int mid=(l+r)>>1; if(mid>=pos) change(k<<1,l,mid,Val,pos); if(mid+1<=pos) change((k<<1)+1,mid+1,r,Val,pos); sum[k]=sum[k<<1]+sum[(k<<1)+1]; Max[k]=max(Max[k<<1],Max[(k<<1)+1]); }
7.查询以u为根结点的子树的信息
void ask_tree(int u){ query(1,1,seg[0],seg[u],seg[u]+size[u]-1); return; }
8.修改以u为根结点的子树的信息
void change_tree(int u){ Change(1,1,seg[0],seg[u],seg[u]+size[u]-1,Val); //因为预处理是dfs,所以每棵子树的结点在线段树上的编号都是连续的 return; }
9.完整树链剖分模板
咕咕咕咕