基本概念
数据项:是描述客观事物的符号,是计算机可以直接操作的对象,是能被计算机识别,并能输入给计算机处理的符号集合
数据元素:是组成数据的、有一定意义的基本单位,在计算机中通常作为整体处理,也被称之为记录
数据项:一个数据元素可以由若干个数据项组成,数据项是数据元素不可分割的最小单位
数据对象:是性质相同的数据元素的集合,是数据的子集
数据结构:是相互之间存在一种或者多种特定关系的数据元素集合
逻辑结构和物理结构
逻辑结构:是指数据对象中数据元素之间的相互关系,分为以下几种
- 集合结构:数据元素除了同属于一个集合以外,他们之间没有任何其他的关系,
- 线性结构:数据元素之间是一对一的关系(例如一个保存序号的数组)
- 树形结构:数据元素之间存在一种一对多的层次关系(例如文件目录树)
- 图形结构:数据元素是多对多的关系
物理结构:指在内存中的存储顺序
- 顺序存储结构:把数据放在连续的存储单元里,其数据之间的关系和物理关系是一致的(例如 int nNum[3] = {1,2,3};这类数据)
- 链式存储结构:是把数据元素放到任意存储单元里,这组存储单元可以是连续的,也可以不是连续的
算法的事件复杂度
用来衡量算法的优劣
大O阶方法:
1、常数阶
2、线性阶
3、对数阶
4、平方阶
所耗费的时间按复杂度从小到大依次是:
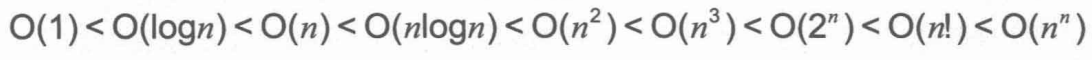
顺序线性表(向量)
基本概念:零个或者多个数据元素的有限序列称为线性表,例如一个字符串就是一个线性表,一个结构体数组也是一个线性表。
- 抽象数据类型
ADT 线性表(List)
Data
除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an除外每个元素有且只有一个后继元素,数据元素之间的关系是一对一的关系
- 存储结构
线性表的顺序存储
1)线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素
2)一般情况下,当我们使用一维数组或者一段连续的缓存来存储一个线性表时,我们称之维线性表的顺序存储结构
3)另外,数据空间的总长度不等于线性表的长度,线性表数据空间的长度指的是此空间可以保存的数据元素的个数,而线性表的长度则指的是线性表实际存贮的数据元素个数
线性表的链式存储:
由于顺序存储结构在执行插入和删除的操作时都需要移动大量的数据,数据量越大,这种存储方式消耗的系统资源就越多,于是就诞生了链式存储结构
1)若线性表需要频繁查找,并且很少做插入域删除操作,则更适合顺序存储结构
2)若线性表中的元素个数变化较大,或根本就不知道有多大时,最好采用链表结构,这样可以无需考虑存储空间的大小问题。
插入和删除元素的区别
顺序线性表的插入和删除:
- 在顺序存储结构下,线性表在插入新数据前需要将其插入点后面的数据依次后移一个单位,以空出位置给新的数据插入
- 在顺序存储结构下,线性表在删除数据后需要将其删除点后面的数据依次前移一个单位,以补足删除后空出的位置
链式线性表的插入和删除:
- 当我们想在链表中插入一个新的数据的时候,只需要申请一段内存空间,然后将其前一个元素的指针指向自己,再将自己的指针指向下一个元素即可,无需操作其他元素
- 当我们想在链表中删除一个节点时,只需要将前一个节点指向后一个节点,并释放掉自己即可。
顺序结构与链式结构的优缺点
顺序存储:将数据元素放于一个连续的存储空间之中,实现顺序存去或者(按下标)直接存取。它的存取效率高,存取速度快。但是它的空间大小一经定义,在程序整个运行期间不会发生改变,因此,不易扩充。同时在删除和插入时,为了保持原有的次序,平均需要移动将近一半元素,修改效率不高。
链式存储:存储的空间一般在程序运行过程中动态分配和释放,且只要存储器中还有空间,就不会产生存储溢出的问题。同时在插入和删除时不需要保持数据元素原来的物理顺序,只需要保持原来的逻辑顺序,因此不必移动数据,只需修改它们的链接指针,效率较高。但存取表中的数据元素时,只能顺序查找后再访问,因此存储效率不高。
链表
-
基本概念
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列节点(链表中每一个元素称之为一个节点)组成,节点可以在运行时动态生成。
每个节点包括两个部份,一个是存储数据区域的数据域,另一个是存储下一个节点地址的指针域
循环链表是另一种形式的的链式存储结构。它的特点是表中最后一个节点的指针域指向头节点,整个链表形成一个环
-
最简单链表---单链表的定义
链表中最简单的一种是单向链表,它包含两个域,一个是数据域和一个指针域。这个链接指向列表中的下一个节点,而最后一个节点则指向一个空值
单向链表通常由一个头指针(head),用于指向链表头
单向链表有一个尾节点,该节点的指针部份指向一个空节点(NULL)
-
单链表的基本操作
对链表的基本操作有:
-
创建链表是指从无到有地建立起一个链表,即往空链接表中依次插入若干节点,并保持节点之间的前驱和后继关系
-
检索操作是指,按给定的几点索引号或检索条件,查找某个节点,如果找到指定的节点,则称为检索成功,否则检索失败
-
插入操作是指,在节点之间插入一个新的节点,使线性表的长度增1
-
删除操作是指,删除节点ki,使线性表的长度减1
-
打印输出
-
单链表模板形式的类定义域实现
#pragma once
#define LI_SUCCESS 0
#define LI_WRONG_LOC 1
#define LI_EMPTY 2
template <class T_LK>
class CLinkList
{
public:
CLinkList();
~CLinkList();
public:
typedef struct _NODE
{
T_LK Data;
_NODE* pNext;
}NODE, *PNODE;
public:
/*****判断链表是否为空*****/
bool IsEmpty();
// 返回链表长度
int Length();
// 清空链表
void Clear();
// 获取索引处元素的内容
bool GetEle(
int Index, // 参数0:索引值
T_LK &Data // 获取值的变量
);
// 获取内容为Data的第一个元素的位置
int GetLoc(
T_LK Data // 参数0:获取值的变量
);
// 在链表的某一个位置插入一个节点
bool ListInsert(
int nLoc, // 参数0:要插入的位置
T_LK nData, // 参数1:要插入的数据
int& nError // 参数2:用于获得一个错误码
);
// 在链表的某一个位置删除一个数据,并返回被删除数据
bool DeleteData(
int nLoc, // 参数0:要删除的位置
T_LK &nData, // 参数1:要删除的数据
int& nError // 参数2:用于获得一个错误码
);
private:
PNODE m_pHead;
int m_nLenth;
};
template<class T_LK>
CLinkList<T_LK>::CLinkList():m_pHead(nullptr), m_nLenth(0) {}
template<class T_LK>
CLinkList<T_LK>::~CLinkList(){}
template<class T_LK>
bool CLinkList<T_LK>::IsEmpty()
{
return (m_nLenth == 0) ? true : false;
}
template<class T_LK>
int CLinkList<T_LK>::Length()
{
return m_nLenth;
}
// 清空链表
template<class T_LK>
void CLinkList<T_LK>::Clear()
{
// 判断是否为空
if (m_pHead == nullptr || m_nLenth == 0)
{
return;
}
// 不为空时,开始清空链表
PNODE Temp = m_pHead;
while (Temp->pNext)
{
m_pHead = Temp->pNext;
delete Temp;
Temp = m_pHead;
}
// 删除最后一个节点,并将链表长度置为0
delete m_pHead;
m_pHead = nullptr;
m_nLenth = 0;
}
// 获取索引处元素的内容
template<class T_LK>
bool CLinkList<T_LK>::GetEle(int Index, T_LK & Data)
{
// 1. 判断链表是否为空
if (m_pHead == nullptr || m_nLenth == 0)
{
return false;
}
// 2. 判断索引是否超出范围
if (Index > m_nLenth || Index == 0)
{
return false;
}
// 3. 循环开始查找索引点
PNODE pTemp = m_pHead;
for (int i = 0; i < Index; ++i)
{
pTemp = pTemp->pNext;
}
// 4. 将元素赋值传出元素
memcpy_s(&Data, sizeof(T_LK), &pTemp->Data, sizeof(T_LK));
return true;
}
// 获取内容为Data的第一个元素的位置
template<class T_LK>
int CLinkList<T_LK>::GetLoc(T_LK Data)
{
// 1.判断链表是否为空
if (m_pHead == nullptr || m_nLenth == 0)
{
return -1;
}
// 2. 循环匹配链表内容,匹配到返回i的值
PNODE pTemp = m_pHead;
for (int i = 1; i <= m_nLenth; ++i)
{
if (!memcmp(&Data, &pTemp->Data, sizeof(T_LK)))
{
return i;
}
pTemp = pTemp.pNext;
}
// 没有找到 返回-1
return -1;
}
// 在链表的某一个位置插入一个节点
template<class T_LK>
bool CLinkList<T_LK>::ListInsert(int nLoc, T_LK nData, int & nError)
{
// 1. 判断插入的位置是否正确
if (nLoc > m_nLenth)
{
nError = LI_WRONG_LOC;
return false;
}
// 2. 判断一下头节点是否为空,为空的话,直接在头节点插入数据
if (m_pHead = nullptr)
{
m_pHead = new NODE;
m_pHead->pNext = nullptr;
m_pHead->Data = nData;
nError = LI_SUCCESS;
m_nLenth++;
return true;
}
// 3. 找到插入的位置
// 3.1 找到插入位置的前一个结点
PNODE Pre = m_pHead;
PNODE PTemp = new NODE;
PTemp->Data = nData;
PTemp->pNext = nullptr;
// 3.2 判断是否是向头节点以前插入,处理特殊情况
if (nLoc == 0)
{
PTemp->pNext = m_pHead;
m_pHead = PTemp;
nError = LI_SUCCESS;
m_nLenth++;
return true;
}
// 3.3 正常情况的插入
for (int i = 0; i < nLoc; i++)
{
Pre = Pre->pNext;
}
// 4. 执行插入的操作
PTemp->pNext = Pre->pNext;
Pre->pNext = PTemp;
// 5. 插入成功 长度自增并返回
nError = LI_SUCCESS;
m_nLenth++;
return true;
}
// 在链表的某一个位置删除一个数据,并返回被删除数据
template<class T_LK>
bool CLinkList<T_LK>::DeleteData(int nLoc, T_LK & nData, int & nError)
{
// 1. 判断链表是不是空
if (m_pHead == nullptr)
{
nError = LI_EMPTY;
return false;
}
// 2. 判断删除的位置是不是错误的
if (nLoc > m_nLenth)
{
nError = LI_EMPTY;
return false;
}
// 3. 找到要删除的位置
// 3.1 要删除的是头节点
if (nLoc == 0)
{
// 给传出的数据赋值
nData = m_pHead->Data;
// 用一个临时变量存储要被释放的头节点
PNODE pTemp = m_pHead;
// 头节点指针指向下一个节点
m_pHead = m_pHead->pNext;
// 释放被删除的节点
delete pTemp;
// 处理后面的事情
pTemp = nullptr;
m_nLenth--;
nError = LI_SUCCESS;
return true;
}
// 3.2 正常的情况下,需要循环找到被删除节点的前一个节点
PNODE pPre = m_pHead;
PNODE pTemp = nullptr;
for (int i = 0; i < nLoc - 1; i++)
{
pPre = pPre->pNext;
}
// 4 开始删除
// 将要删除的节点的地址存储到临时变量中
pTemp = pPre->pNext;
// 为传出的数据赋值
nData = pTemp->Data;
// 将被删除的前一个节点和被删除的后一个节点连起来
pPre->pNext = pPre->pNext->pNext;
delete pTemp;
pTemp = nullptr;
// 5. 删除成功,填写错误码,长度自减并返回
m_nLenth--;
nError = LI_SUCCESS;
return true;
}