图的存储方式

图的存储方式：

　　　　　一、邻阶矩阵：　　

　　　　　　这个名字看起来高大上， 其实他就是数值。

　　　　　　我们所学的图就是 点与点之间的关系， 所以 数组的纵向表示起点， 横向表示终点， 两个点之间相连，就标记为1， 否则标记为0.

　　　　　　NPNBB（no picture no bi bi  没有图片别bb）↓

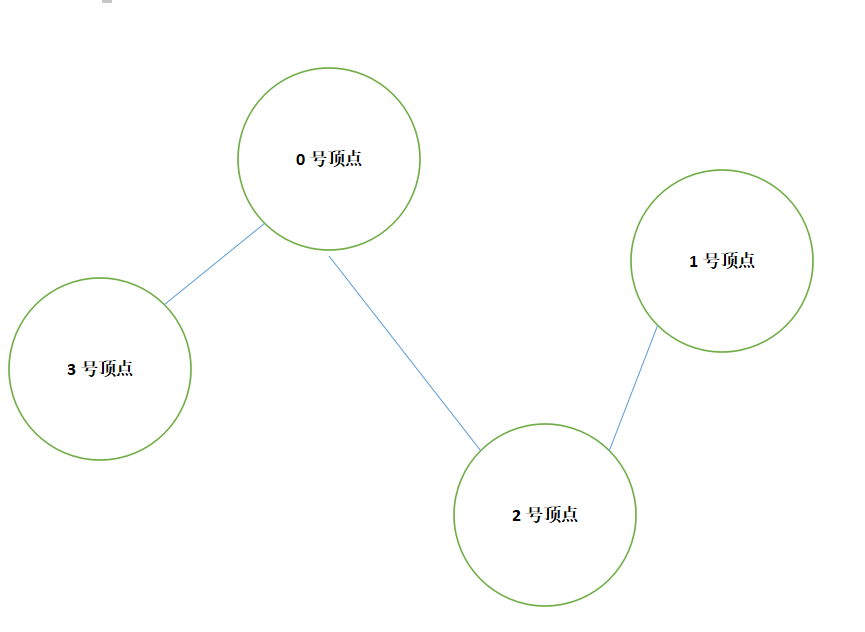
　　　　此图为无向图， 连线有  0 　　3， 0　　2，1　　2.

　　　　因为有4个顶点， 所以4*4的二维数组 map[4][4]。

 　　　　①首先初始化都为零 

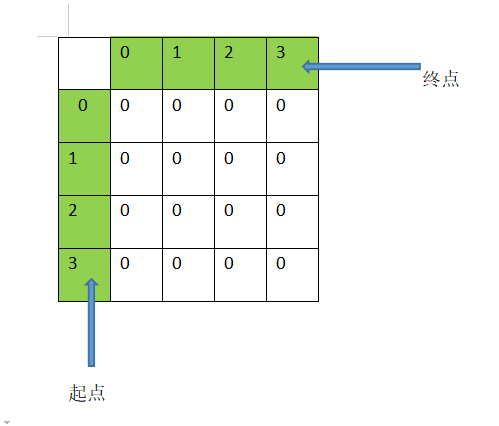
　　　　②如果连接相应的map[i][j]标记为1（无向图 map[j][i] 也要标记 1）。

————邻接矩阵的优点就是操作简单， 然而都顶点较多时， 邻接矩阵就会太占内存。

　　　　并且邻接矩阵的时间复杂度是O（n^2+e），（e条边）， 所以在创建图时很耗时间。

　　　　二、邻接表

　　　　　　邻接表， 是通过链表来实现的， 在顶点数量多时， 邻接表相对会有优势。

　　　　　　1、首先邻接表组成：

　　　　　　①表头（也可叫他：顶点表）。

　　　　　　

struct VerNode//表头
{
    int data;//（如果表头， 是数组这里用不到， 是链表，这里储存顶点的下标）      
    struct EdgeNode *first;//指向第一个表边。  
}

　　

　　　　　　②表边（或者边表）。

　　　　　　

struct EdgeNode//表边
{
      int  data；//储存终点的下标
      struct  EdgeNode *next;//指向下一个表边    
}

　　　　什么是表头， 顾名思义， 就是一条线的顶点， 表边就是用来储存终点的。

　　　　表头可以用数组开辟（这样查找等操作方便）， 也可以用单项链表。

　　　　2、操作。

　　　　　　还是之前那个图，0　　3相连（这里以0　　3 为）

　　　　　　

scanf("%d %d", &i, &j);//输入边
struct EdgeNode *E;//定义一个表边指针
E = (struct EdgeNode *)malloc(sizeof(struct node));//申请空间
E->data = j;//储存边的终点
//连接操作
E->next = V[i].first;//指向表边、头的first
V[i].first = E;//表头再指向新的表边

　　　　　　　邻接表在创建图时， 时间复杂度是（n+e）。（n个顶点（因为顶点都要初始化）， e条边）

三、边集数组

　　边集数组是图的另一种存储方式， 简单的说就是一个数组储存着边的起点，终点和权值。

struct Edge//边数组
{
     int f;//边的起点
     int t;//边的终点
     int w;//权值
}

int v【100】；//顶点数组

　

  　　按照开始给的图用边集数组表示就是这样

　　　

 四、前向星

　　前向星是一个特殊的边集数组， 其特殊性在于他在边集数组的基础上，按照起点进行了一次排序， 优点（相同的起点的边， 就可以邻在一起）。

五、利用c++中vector的 特点（动态数组）来存图；

　　　　

struct Edge//边表
{
     int v;//终点
     int w;//权值  
}；

vector<Edge>G[N];//N表示顶点的数量；

其实， vector 很想 邻接表， 相比邻接表（Edge结构体是边表， vector 是一个 Edge类型 的二维动态数组， 相当于 ）， 他写起来比邻接表更方便。

这种方法很多人叫他（vector + 前向星）。