9大背包第二弹 | 完全背包

---

 学习链接：01背包问题和完全背包问题、背包问题九讲笔记_完全背包

本文测试数据以及参考学习链接：经典背包问题 01背包+完全背包+多重背包

---

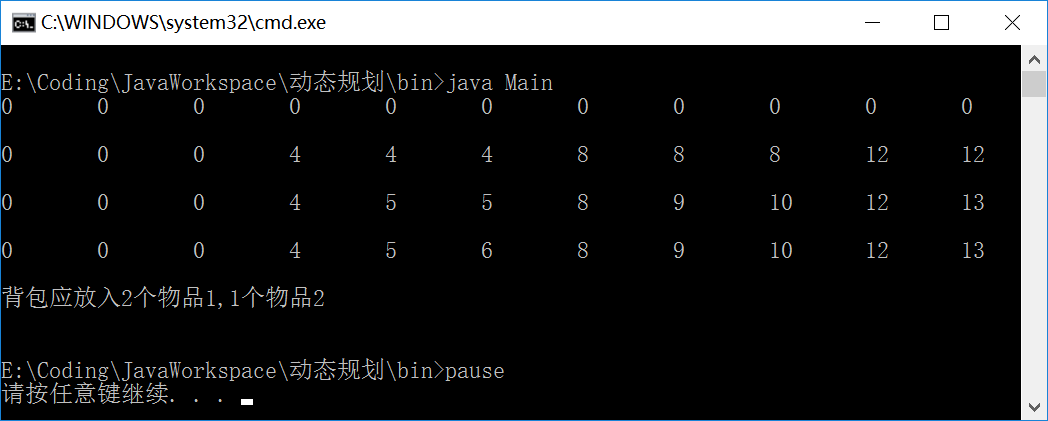
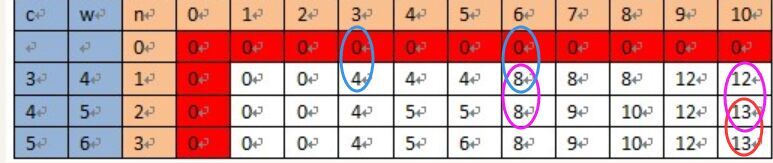
测试数据：

 int[]w={3,4,5};//物品重量
int[]v={4,5,6};//物品价值
背包总重量：10
求解矩阵：

---

用求解矩阵反求解向量x[]

---

java代码：

import java.util.*;

public class Main {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
/*        double []w={2,2,6,5,4};
        double []v={6,3,5,4,6};
        double weight=10;
        _01package problem=new _01package(w,v,weight);*/
        int[]w={3,4,5};//物品重量
        int[]v={4,5,6};//物品价值
        int weight=10;
        Complete_package problem=new Complete_package(w,v,weight);
        problem.solve();
        System.out.println(problem);
    }
}

class Complete_package{//完全背包
    int[][] matrix;//求解矩阵
    int []v;//价值向量
    int []w;//重量向量
    int []x;//规划结果
    int N;
    int weight;//背包上限
    Complete_package(int[]w,int[]v,int weight){
        this.w=w;
        this.v=v;
        this.weight=weight;
        N=w.length;
        x=new int[N];
        matrix=new int[N+1][weight+1];//构造求解矩阵
        int i;
        for(i=0;i<N+1;i++){
            matrix[i][0]=0;//第一列为0
        }
        for(i=0;i<weight+1;i++){
            matrix[0][i]=0;//第一行为0
        }
    }
    void solve(){
        int i,j,k;
        for(i=1;i<N+1;i++){//对于所有物品
            for(j=1;j<weight+1;j++){//背包的容量在不多增长
                if(w[i-1]<=j){//如果物品能放入背包
                    int max=matrix[i-1][j];//不放入物品的情况
                    //强行放入物品
                    int count=weight/w[i-1];
                    for(k=1;k<=count+1;k++){
                        if(j-k*w[i-1]<0)break;
                        max=Math.max(matrix[i-1][j-k*w[i-1]]+k*v[i-1],
                                                max);
                    }
                    matrix[i][j]=max;
                }else{
                    matrix[i][j]=matrix[i-1][j];
                }
            }
        }
        traceBack();
    }
    void traceBack(){
        int i,j;
        j=weight;
        for(i=0;i<N;i++){
            x[i]=0;//对解向量进行初始化
        }
        for(i=N;i>0;i--){//对物品从下向上遍历
            int tmp=matrix[i][j];
            int tmp1=matrix[i-1][j];
            //若不等，则循环
            while(matrix[i][j]!=matrix[i-1][j]){//直到放入物品前后背包的价值不再变化
                j-=w[i-1];
                x[i-1]++;
            }
        }
    }
    public String toString(){
        int row = matrix.length;//行数
        int col =matrix[0].length;//列数
        String str=new String("");
        int i,j;
        for(i=0;i<row;i++){
            for(j=0;j<col;j++){
                str+=Integer.toString(matrix[i][j]);
                str+="	";
            }
            str+="

";
        }
        str+="背包应放入";
        for(i=0;i<N;i++){
            if (x[i]!=0) {
                str+=x[i]+"个物品"+(i+1)+",";
            }
        }
        str=str.substring(0, str.length()-1);
        str+="
";
        return str;
    }
}

---

输出：