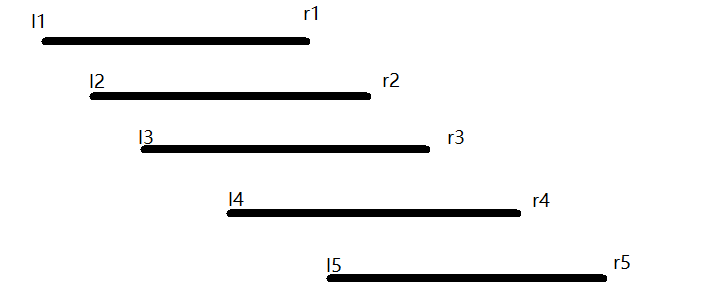【HEOI 2018】制胡窜

转载请注明出处:http://www.cnblogs.com/TSHugh/p/8779709.html

YJQ的题解把思路介绍得很明白,只不过有些细节说得还是太笼统了(不过正经的题解就应该这个样子吧).
我的思路和YJQ有一些不同.
首先:

考虑反过来,求三个串都不包含询问串的方案数,这样需要的讨论会少很多.不难发现,三个串都不包含询问串的方案,就是询问串每个出现位置里(这里的位置指的是整个串,不是右端点),都至少含有一个断点的方案数.(本段落来自YJQ题解)

然后:

可以发现割的话一定是把原来的一群线段分为两波(其中某一波可以为0),假设左边的那刀为第一刀,右边的那刀为第二刀,第一波均由第一刀砍断,第二波均由第二刀砍断.
考虑如何通过划分两波线段来计算方案数.
设共匹配了m条线段,且这些线段按照位置依次排列,位置最靠前的线段为1,位置最靠后的线段为m.
考虑第一刀的位置.第一刀的位置显然是1往左,或者1上,因为如果是1往右的话是一定是切不断1的.
先看第一刀的位置在1往左的时候.这个时候第二刀必须切在所有线段的交上.这个可以很容易的判断和计算.

再来看第一刀的位置在1上的时候.先看一下上面那张图(图片来自YJQ题解),图中的1被下面线段的左端点分为了几部分——[l1,l2)、[l2,l3)、[l3,l4)、[l4,r1].不妨把1被分为的部分分为最后一段和不是最后一段两种.
先看不是最后一段的部分.每一段的贡献是|[l[i],l[i+1])|*|i+1与m的交|.写成公式就是∑(r[i+1]-r[i])*(r[i+1]-l[m]),括号拆开,所求即∑(r[i+1]-r[i])*r[i+1]与∑(r[i+1]-r[i]).(本段内容整理自YJQ题解)
再来看最后一段.考虑这一段的贡献,如果这一段是所有线段的交,那么贡献就可以用等差数列求前缀和求得,如果不是的话贡献就是|[l[i],r[1]]|*|i+1与m的交|.

(以上思路中的公式可能需要一定的微调,具体公式请读者在懂得思路后自行推断.)
以上就是我这道题思路的全部了.实现的话我用的是SAM和替罪羊启发式合并,竟然比线段树合并快……

#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long LL;
const int A=20;
const int N=100010;
const int M=300010;
const int Inf=0x3f3f3f3f;
const double alpha=0.75;
int n,m;
LL ans[M];
char s[N];
struct Q{
  int to,next,id;
}q[M];
int mine[N<<1],qt;
inline void add(int x,int y,int z){
  q[++qt].to=y,q[qt].next=mine[x],mine[x]=qt,q[qt].id=z;
}
struct V{
  int to,next;
}c[N<<1];
int head[N<<1],t;
inline void add(int x,int y){
  c[++t].to=y,c[t].next=head[x],head[x]=t;
}
struct ScapeGoat_Tree{
  ScapeGoat_Tree *ch[2];
  int size;
  int key,max,min;
  LL sum1,val1;
  int sum2,val2;
  inline void pushup(){
    size=ch[0]->size+ch[1]->size+1;
    sum1=ch[0]->sum1+ch[1]->sum1+val1;
    sum2=ch[0]->sum2+ch[1]->sum2+val2;
    max=min=key;
    max=std::max(max,ch[0]->max);
    max=std::max(max,ch[1]->max);
    min=std::min(min,ch[0]->min);
    min=std::min(min,ch[1]->min);
  }
  inline bool isbad(){
    return size*alpha+5<ch[0]->size||size*alpha+5<ch[1]->size;
  }
  inline void* operator new(size_t);
}*root[N<<1],*null,*C,*mempool,*list[N];
inline void* ScapeGoat_Tree::operator new(size_t){
  if(C==mempool){
    C=new ScapeGoat_Tree[(1<<15)+10];
    mempool=C+(1<<15)+10;
  }
  return C++;
}
int len;
inline void travel(ScapeGoat_Tree *p){
  if(p==null)return;
  travel(p->ch[0]);
  list[++len]=p;
  travel(p->ch[1]);
}
inline ScapeGoat_Tree *divide(int l,int r){
  if(l>r)return null;
  int mid=(l+r)>>1;
  list[mid]->ch[0]=divide(l,mid-1);
  list[mid]->ch[1]=divide(mid+1,r);
  list[mid]->pushup();
  return list[mid];
}
inline void rebuild(ScapeGoat_Tree *&p){
  if(p==null)return;
  len=0;
  travel(p);
  p=divide(1,len);
}
inline ScapeGoat_Tree **insert(ScapeGoat_Tree *&p,int key,LL val1,int val2){
  if(p==null){
    p=new ScapeGoat_Tree;
    p->ch[0]=p->ch[1]=null;
    p->size=1;
    p->key=p->max=p->min=key;
    p->sum1=p->val1=val1;
    p->sum2=p->val2=val2;
    return &null;
  }
  ScapeGoat_Tree **ret=insert(p->ch[key>p->key],key,val1,val2);
  p->pushup();
  if(p->isbad())ret=&p;
  return ret;
}
inline void Insert(ScapeGoat_Tree *&p,int key,LL val1,int val2){
  rebuild(*insert(p,key,val1,val2));
}
inline void update(ScapeGoat_Tree *p,int key){
  if(p==null)return;
  if(p->key<=key)update(p->ch[1],key);
  else{
    if(p->ch[0]->size==0||p->ch[0]->max<=key){
      p->val1=(LL)p->key*(p->key-key);
      p->val2=p->key-key;
    }else update(p->ch[0],key);
  }
  p->pushup();
}
inline int upper_bound(ScapeGoat_Tree *p,int key){
  if(p==null)return 0;
  if(p->key<=key)return upper_bound(p->ch[1],key);
  else{
    if(p->ch[0]->size==0||p->ch[0]->max<=key)return p->key;
    else return upper_bound(p->ch[0],key);
  }
}
inline int lower_bound(ScapeGoat_Tree *p,int key){
  if(p==null)return 0;
  if(p->key>=key)return lower_bound(p->ch[0],key);
  else{
    if(p->ch[1]->size==0||p->ch[1]->min>=key)return p->key;
    else return lower_bound(p->ch[1],key);
  }
}
inline void Insert(ScapeGoat_Tree *&p,int key){
  update(p,key);
  int pr=lower_bound(p,key);
  Insert(p,key,pr?(LL)(key-pr)*key:0,pr?key-pr:0);
}
inline void query(ScapeGoat_Tree *p,int key,LL &sum,int &size){
  if(p==null)return;
  if(p->key<=key){
    sum+=p->ch[0]->sum1+p->val1;
    size+=p->ch[0]->sum2+p->val2;
    query(p->ch[1],key,sum,size);
  }else
    query(p->ch[0],key,sum,size);
}
inline LL query(ScapeGoat_Tree *p,int len){
  int r1=p->min,rn=p->max,ln=rn-len+1;
  LL sum1=0,sum2=0,ret=0;
  int size1=0,size2=0;
  query(p,r1+len-2,sum1,size1);
  query(p,ln,sum2,size2);
  if(size1<=size2)ret=0;
  else ret=sum1-sum2-(LL)(size1-size2)*ln;
  if(ln<r1)ret+=(LL)(r1-len)*(r1-ln);
  int prv=lower_bound(p,r1+len-1),nxt=upper_bound(p,prv);
  if(!nxt)ret+=(LL)((n-ln-1)+(n-r1))*(r1-ln)>>1;
  else ret+=(LL)(r1-(prv-len+1))*std::max(nxt-ln,0);
  return ret;
}
inline void dfs(ScapeGoat_Tree *p,ScapeGoat_Tree *&to){
  if(p==null)return;
  Insert(to,p->key);
  dfs(p->ch[0],to);
  dfs(p->ch[1],to);
}
int rt,sz,trans[N<<1][10],link[N<<1],max[N<<1],f[N<<1][A],pos[N];
#define newnode(a) (max[++sz]=(a),sz)
inline int insert(int x,int last){
  int w=last,nw=newnode(max[w]+1),h,nh;
  while(w&&!trans[w][x])trans[w][x]=nw,w=link[w];
  if(!w)
    link[nw]=rt;
  else{
    h=trans[w][x];
    if(max[h]==max[w]+1)
      link[nw]=h;
    else{
      nh=newnode(max[w]+1);
      memcpy(trans[nh],trans[h],40);
      while(w&&trans[w][x]==h)trans[w][x]=nh,w=link[w];
      link[nh]=link[h],link[nw]=link[h]=nh;
    }
  }
  return nw;
}
inline void dfs(int x,int fa){
  int i;
  f[x][0]=fa;
  root[x]=null;
  for(i=1;i<A;++i)
    f[x][i]=f[f[x][i-1]][i-1];
  for(i=head[x];i;i=c[i].next)
    dfs(c[i].to,x);
}
inline int ipos(int x,int len){
  int i;
  for(i=A-1;i>=0;--i)
    if(max[f[x][i]]>=len)
      x=f[x][i];
  return x;
}
inline void dfs(int x){
  int i,j,v;
  for(i=head[x];i;i=c[i].next){
    v=c[i].to;
    dfs(v);
    if(root[x]->size<root[v]->size)
      std::swap(root[v],root[x]);
    dfs(root[v],root[x]);
  }
  for(i=mine[x];i;i=q[i].next)
    ans[q[i].id]=query(root[x],q[i].to);
}
int main(){
  rt=newnode(0);
  null=new ScapeGoat_Tree;
  memset(null,0,sizeof(*null));
  null->ch[0]=null->ch[1]=null;
  null->min=Inf,null->max=-Inf;
  scanf("%d%d",&n,&m);
  scanf("%s",s+1);
  int i,last=rt,l,r,x;
  for(i=1;i<=n;++i)
    last=pos[i]=insert(s[i]-'0',last);
  for(i=2;i<=sz;++i)
    add(link[i],i);
  dfs(1,0);
  for(i=1;i<=n;++i)
    Insert(root[pos[i]],i);
  for(i=1;i<=m;++i){
    scanf("%d%d",&l,&r);
    x=ipos(pos[r],r-l+1);
    add(x,r-l+1,i);
  }
  dfs(1);
  LL sum=(LL)(n-2)*(n-1)>>1;
  for(i=1;i<=m;++i)
    printf("%lld
",sum-ans[i]);
  return 0;
}