先来学习P神放点P
本文是看了黄源河的论文后才写的
如果本人有哪些地方写得不对的,希望各位大佬改正ORZ
学习C++的大佬应该都会优先队列(原谅我的菜,我连priority_queue都不会拼)
左偏树说到底就是一个升级版的堆
因为左偏树拥有所有堆拥有的功能比如说插入一个节点,取出堆顶和删除堆顶
我们的左偏树的优秀到底体现在哪呢?
左偏树可以合并两个堆!!!
如果我们用普通的做法合并两个堆是需要O(N)的时间
那么如果合并操作非常多
那么堆就不在实用了
左偏树的定义及其性质
先来规定左偏树的一些概念
外节点:一个没有右儿子的节点成为外节点
dist[u]:表示在它的儿子中,离它最近的外节点与它的距离
如果u本身就是一个外节点,那么dist[u]=0
如果u节点不存在(也就是空节点),那么dist[u]=-1
左偏树的性质有哪些呢
性质1:节点的键值小于等于它的左右儿子的键值(这是由堆的性质推导出来的,当然这里也可以是大于等于,那么这就是大根堆了)
根据性质1,我们可以轻而易举地证明从左偏树中取最小(最大)值的时间复杂度是O(1)的
性质2:对于一个节点,设它的左儿子为Left,右儿子为Right,那么有dist[Left] >=dist[Right] 这条性质也被成为左偏性质
如果一个节点它只有右儿子,却没有左儿子,这种情况是不存在的
因为dist[Left]=-1,而dist[Right]=0
不符合左偏树的性质,所以我们也可以通过这个性质看出来,在一棵左偏树中,不存在只有右儿子的节点
所以左偏树的命名也由此而来,因为所有的儿子都在往左偏靠拢
性质3:dist[u]=dist[right(u)] + 1
这个是需要证明的,但是论文里并没有提到它的证明
所以我参考了阿波罗大佬的
好吧,其实这很简单
其实我们根据定义,可以发现dist[u]=min(dist[left(u)],dist[right(u)]) + 1
但是根据左偏树的性质,我们可以发现,dist[left(u)] >= dist[right(u)]
所以dist[u]=dist[right(u)] + 1
哇~So easy
这也可以间接证明为什么空节点的dist要定为-1
这里有一个引理:如果一棵左偏树的根的距离是已知的,那么当这棵树节点最少时,一定是一棵完全二叉树
我们假定这棵树的距离为K
当对于所有的u都满足dist[left(u)] = dist[right(u)] 时,这棵树的深度最小为K
所以这棵树节点最少就是2K+1 - 1
性质4:存在一个N个节点的左偏树,它的距离最大为log2(N+1) -1
这个定理由上面的引理可以推出
N >= 2K+1 - 1
N + 1 >= 2K+1
两边同时log2
就变成了log2(N+1) >= K + 1
所以 K <= log2(N+1) -1
左偏树的操作
我们先假定我们原来的堆是一个小根堆
讲完了左偏树的性质
我们来看看如何使它是如何升级为优先队列2.0的吧
首先我们要讲到的是左偏树中,最最最最关键的Merge操作
这个操作是左偏树中最基础的操作
Merge顾名思义,就是合并两个堆,这也是左偏树的升级之处
我们定义Merge(A,B)是一个函数,A,B是两棵左偏树(???),返回值是一棵合并好了的左偏树
这个函数的边界情况非常地好考虑,就是A,B中的任意一棵树为空,那么我们就应该返回不为空的那棵子树
我们的目的就是将B合并到A的右儿子的位置上,所以A的根节点的键值是需要<=B的根节点的键值的
否则的话,我们将A,B两棵树交换位置
我们接下去就递归调用Merge(right(A),B)
我们会发现对于Merge好了的一棵左偏树,我们就会怀疑这棵树是否还满足左偏树的性质——dist[left(u)] >= dist[right(u)]
如果不符合,我们交换A的左右子树
最后由于整棵树已经彻底改变了模样~~~
所以我们就需要更新A的距离了
dist[A]=dist[right(A)] + 1
代码流程大致这样
如果我们需要把一个新节点B加入到A中,我们把这个操作叫做Insert(A,B)
其实我们大可将B看做Merge中的一棵树
因此Insert(A,B)与Merge(A,B)是一样的

如果我们需要取最小值并且删除它的话,我们定义这个函数为DeleteMin(A)
首先我们需要先求出A这棵树中的根的键值,就是Key[root(A)]
然后我们直接将根删除,剩下的两棵子树,我们就可以直接进行Merge操作了

以上就是最基础的左偏树了
最后来吹嘘一下左偏树的好
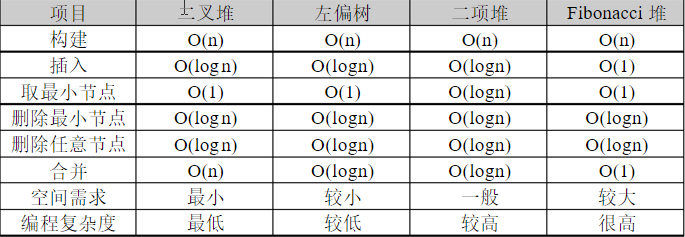
不得不说,左偏树在现实中还是非常实用的
建议多去写写
这里有几道左偏树的练习题
第一道HDU4006-The Kth Greatest Number
左偏树果然是一个非常神奇的东西
HDU1512-Monkey King 题解戳这里
李沁么么哒
李沁好美啊