POJ 2635 The Embarrassed Cryptographer (千进制，素数筛，同余定理）

The Embarrassed Cryptographer

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 15767		Accepted: 4337

Description

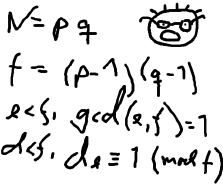The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively.
What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10¹⁰⁰ and 2 <= L <= 10⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10
143 20
667 20
667 30
2573 30
2573 40
0 0

Sample Output

GOOD
BAD 11
GOOD
BAD 23
GOOD
BAD 31
这个题最大的亮点就是利用千进制，100位只能这样。
很有意思的推论，利用同余定理，记住原理吧，这个规律挺神奇的，所以数学还挺好玩的
    同余公式也有许多我们常见的定律,比如相等律,结合律,交换律,传递律….如下面的表示:

•    　　1)a≡a(modd)

•    　　2)a≡b(modd)→b≡a(mod d)

•    　　3)(a≡b(modd),b≡c(mod d))→a≡c(mod d)

•    　　如果a≡x(modd),b≡m(mod d),则

•    　　4)a+b≡x+m （mod d）

•    　　5)a-b≡x-m(mod d)

•    　　6)a*b≡x*m(mod d )

•    　　

应用：

•    (a+b)%c=(a%c+b%c)%c;

•    (a*b)%c=(a%c*b%c)%c;

•    对于大数的求余，联想到进制转换时的方法，得到

•    举例如下，设大数 m=1234,模n

•    就等于((((1*10)%n+2%n)%n*10%n+3%n)%n*10%n+4%n)%n

大数求余的简单模板：

•    #include<stdio.h>//大数求余，其中n(除数）不是大数
char a[1000];
int main()
 int i,j,k,m,n;
{
 while(scanf("%s%d",a,&n)!=EOF)
 {
  m=0;
  for(i=0;a[i]!='';i++)
   m=((m*10)%n+(a[i]-'0')%n)%n;
  printf("%d ",m);
 }
 return 0;
}

同时我是真的手残啊。。。小bug太多了。。真的是在写bug

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include<iostream>
#include <cmath>
#include<string>
#define ll long long 
#define dscan(a) scanf("%d",&a)
#define mem(a,b) memset(a,b,sizeof a)
using namespace std;
#define MAXL 1105
#define Endl endl
#define maxn 1000055
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') {x=10*x+ch-'0';ch=getchar();}
    return x*f;
}
int isp[maxn],p[maxn],cnt;
void getp()
{
    
    int cnt=0;
    for(int i=2;i<=maxn;++i)
    {
        if(!isp[i]) p[cnt++]=i;
        for(int j=0;j<cnt&&p[j]*i<=maxn;++j){
            isp[i*p[j]]=p[j];
            if(i%p[j]==0) break;
        }
    }
}
int num,nums,ks;
int main()
{
    string s;
    int n;
    getp();
    //for(int i=0;i<=10;++i) cout<<p[i]<<" ";
    while(cin>>s>>n&&(s[0]!='0'&&n!=0))
    {
        //cout<<s<<endl;
        int len=s.length();
        int i;
        int flag=1;
        for(i=0;p[i]<n;++i)
        {
            num=0;
            for(int j=0;j<len;j+=3)
            {
               nums=0;
               ks=1;
               for(int k=j;k<j+3&&k<len;k++)
               {
                   ks*=10;
                   nums=nums*10+s[k]-'0';
               }
               num=num*ks+nums;
               //cout<<"num="<<num<<endl;
               num%=p[i];
               //cout<<"num="<<num<<endl;
        }
        if(num==0) {printf("BAD %d
",p[i]);flag=0;break;}
        }
        if(flag) printf("GOOD
");
    }
    return 0;
}