斐波那契数列几种算法及时间复杂度分析

参考：https://blog.csdn.net/beautyofmath/article/details/48184331

https://blog.csdn.net/ecjtu_yuweiwei/article/details/47282457

https://blog.csdn.net/leex_brave/article/details/51490650   递归方式的时间复杂度分析似乎有问题

1.递归

int fibonacci(int n)
{if (n<=0) {
        return  0;
    }
    if (n==1) {
        return 1;
    }
    return fb(n-1)+fb(n-2);
}

关于这种解法，不再赘述，下面主要说下时间复杂度分析。 

设f(n)为参数为n时的时间复杂度，很明显：f(n)=f(n-1)+f(n-2) 
这就转化为了数学上的二阶常系数差分方程，并且为齐次方程。 
即转化为了求f(n)的值，f(n)=f(n-1)+f(n-2)且f(0)=0; f(1)=1; 
特征方程为：x^2-x-1=0 
得 x=(1±√5)/2 
因而f(n)的通解为: 

 

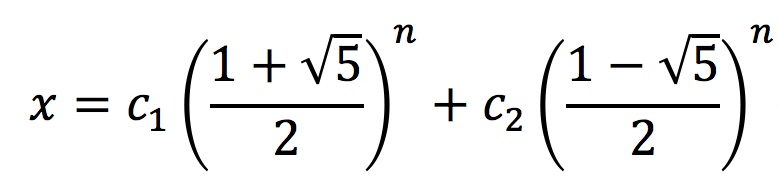
由f(0)=0; f(1)=1可解得c_1，c_2 
最终可得，时间复杂度为： 

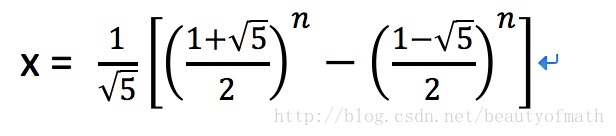
2.循环累计

避免了重复计算，时间复杂度为O（n）。

int Fibonacci(int n) {
        if (n<=0) {
            return 0;
        }
        if (n==1) {
            return 1;
        }
        int min=0;
        int max=1;
        int i=2;
        int result=0;
        while (i<=n) {
            result=min+max;
            min=max;
            max=result;
            ++i;
        }
        return result;
    }

 

3.利用矩阵的乘法

根据递归公式可以得到

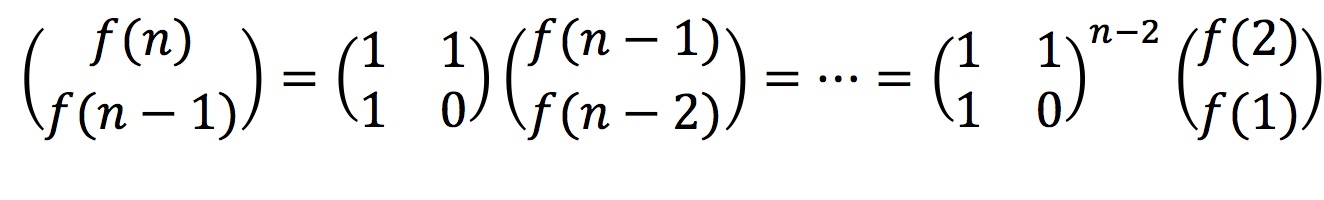
因而计算f(n)就简化为了计算矩阵的(n-2)次方，而计算矩阵的(n-2)次方，我们又可以进行分解，即计算矩阵(n-2)/2次方的平方，逐步分解下去，由于折半计算矩阵次方，因而时间复杂度为O(log n) 。

 

关于矩阵相乘算法可参考上面第三个链接，讲的更为详细。

 

具体代码实现如下：

//
//  main.cpp
//  fibonaccimatrix
//
//  Created by shunagao on 15/8/31.
//  Copyright © 2015年 shunagao. All rights reserved.
//

#include <iostream>
using namespace std;

class Matrix
{
public:
    int n;
    int **m;
    Matrix(int num)
    {
        m=new int*[num];
        for (int i=0; i<num; i++) {
            m[i]=new int[num];
        }
        n=num;
        clear();
    }
    void clear()
    {
        for (int i=0; i<n; ++i) {
            for (int j=0; j<n; ++j) {
                m[i][j]=0;
            }
        }
    }
    void unit()
    {
        clear();
        for (int i=0; i<n; ++i) {
            m[i][i]=1;
        }
    }
    Matrix operator=(const Matrix mtx)
    {
        Matrix(mtx.n);
        for (int i=0; i<mtx.n; ++i) {
            for (int j=0; j<mtx.n; ++j) {
                m[i][j]=mtx.m[i][j];
            }
        }
        return *this;
    }
    Matrix operator*(const Matrix &mtx)
    {
        Matrix result(mtx.n);
        result.clear();
        for (int i=0; i<mtx.n; ++i) {
            for (int j=0; j<mtx.n; ++j) {
                for (int k=0; k<mtx.n; ++k) {
                    result.m[i][j]+=m[i][k]*mtx.m[k][j];
                }   
            }
        }
        return result;
    }
};
int main(int argc, const char * argv[]) {
    unsigned int num=2;
    Matrix first(num);
    first.m[0][0]=1;
    first.m[0][1]=1;
    first.m[1][0]=1;
    first.m[1][1]=0;
    int t;
    cin>>t;
    Matrix result(num);
    result.unit();
    int n=t-2;
    while (n) {
        if (n%2) {
            result=result*first;
            }
        first=first*first;
        n=n/2;
    }
    cout<<(result.m[0][0]+result.m[0][1])<<endl;
    return 0;
}