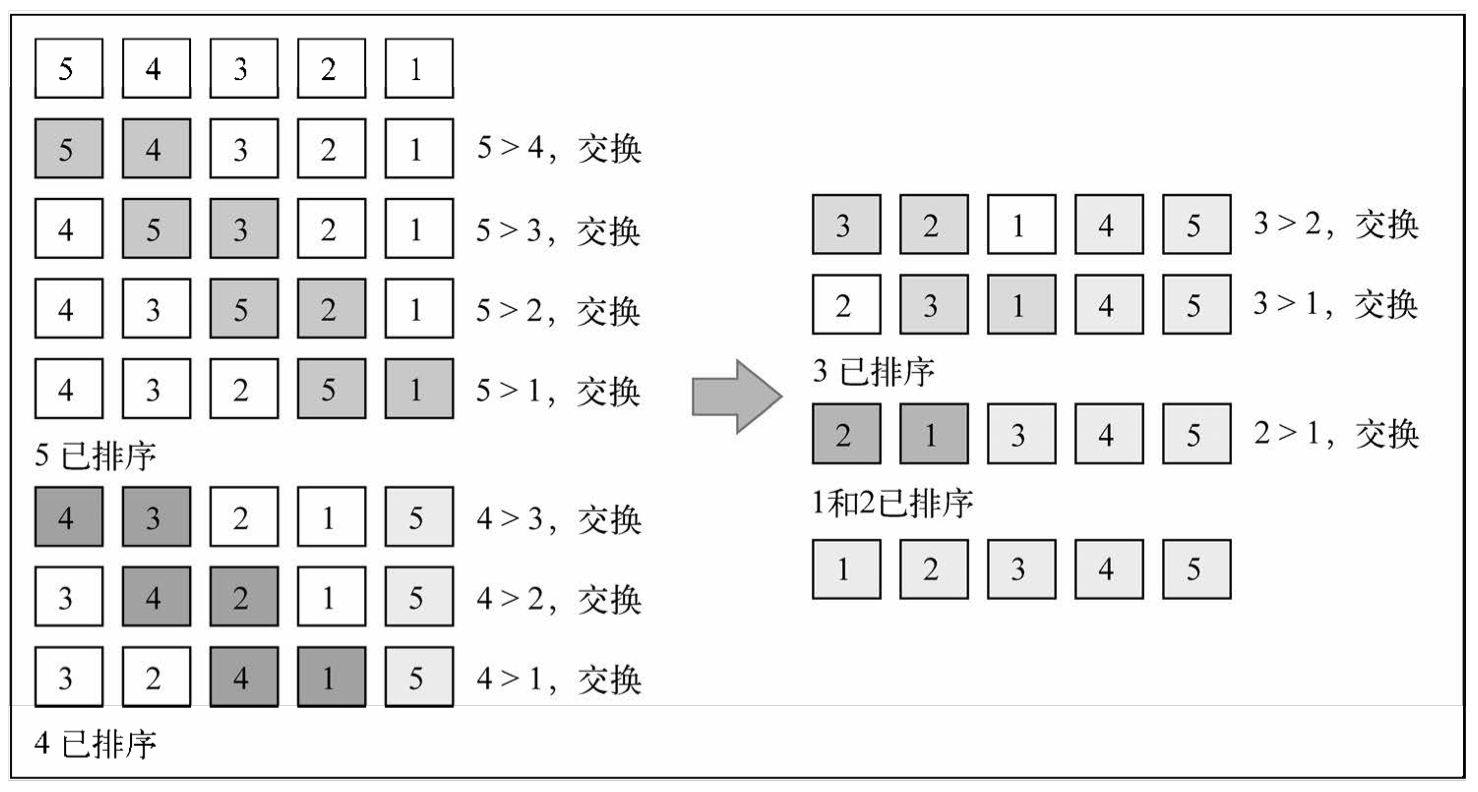
1、冒泡排序
人们开始学习排序算法时,通常都先学冒泡算法,因为它在所有排序算法中最简单。然而, 从运行时间的角度来看,冒泡排序是最差的一个,接下来你会知晓原因。
冒泡排序比较任何两个相邻的项,如果第一个比第二个大,则交换它们。元素项向上移动至 正确的顺序,就好像气泡升至表面一样,冒泡排序因此得名。
冒泡排序算法的复杂度是 O(n²),并不推荐此算法。
Array.prototype.bubbleSort = function () { for (let i = 0; i < this.length; i++) { for (let j = 0; j < this.length - 1 - i; j++) { if (this[j] > this[j + 1]) { let tmp = this[j] this[j] = this[j + 1] this[j + 1] = tmp } } } return this }
2、选择排序法
选择排序算法是一种原址比较排序算法。选择排序算法的思路是:找到数据结构中的最小值并
将其放置在第一位,接着找到第二小的值并将其放在第二位,以此类推。
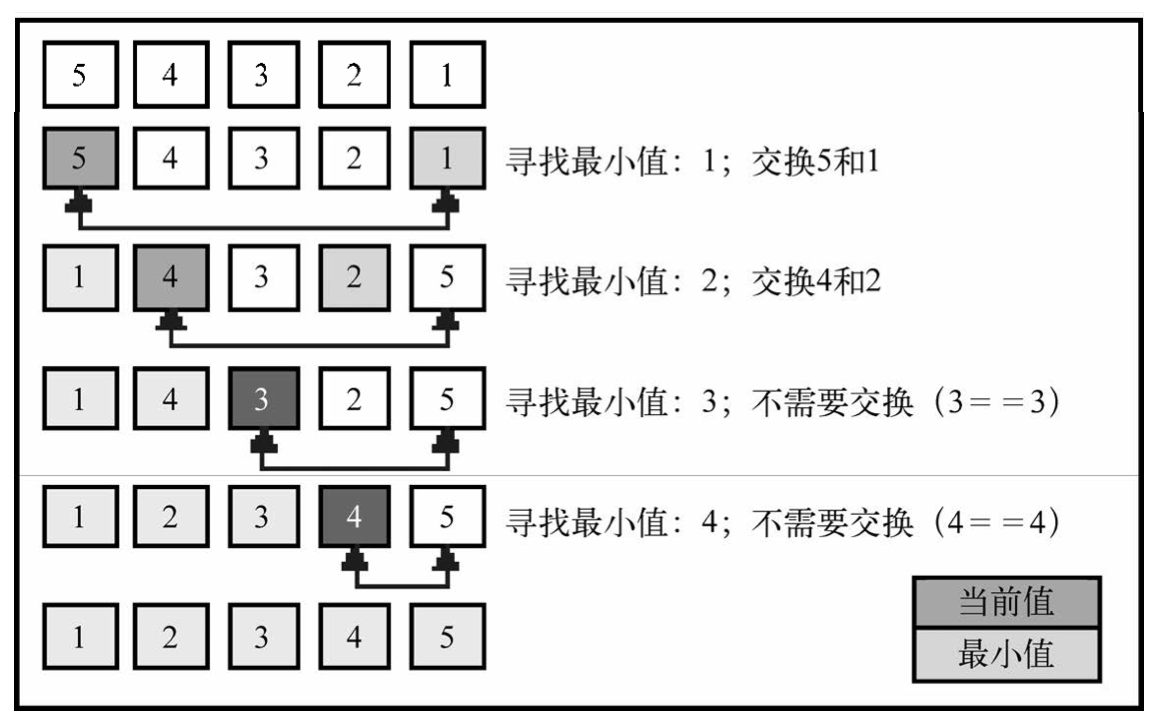
其时间复杂度为 O(N^2)。
虽然选择排序和冒泡排序的时间复杂度一样,但实际上,选择排序进行的交换操作很少,最多会发生 N - 1次交换。
而冒泡排序最坏的情况下要发生N^2 /2交换操作。从这个意义上讲,交换排序的性能略优于冒泡排序。
而且,交换排序比冒泡排序的思想更加直观。
Array.prototype.chooseSort = function () { for (let i = 0; i < this.length; i++) { let minIndex = i for (let j = i + 1; j < this.length; j++) { if (this[j] < this[i]) { minIndex = j } } let tmp = this[i] this[i] = this[minIndex] this[minIndex] = tmp } return this }
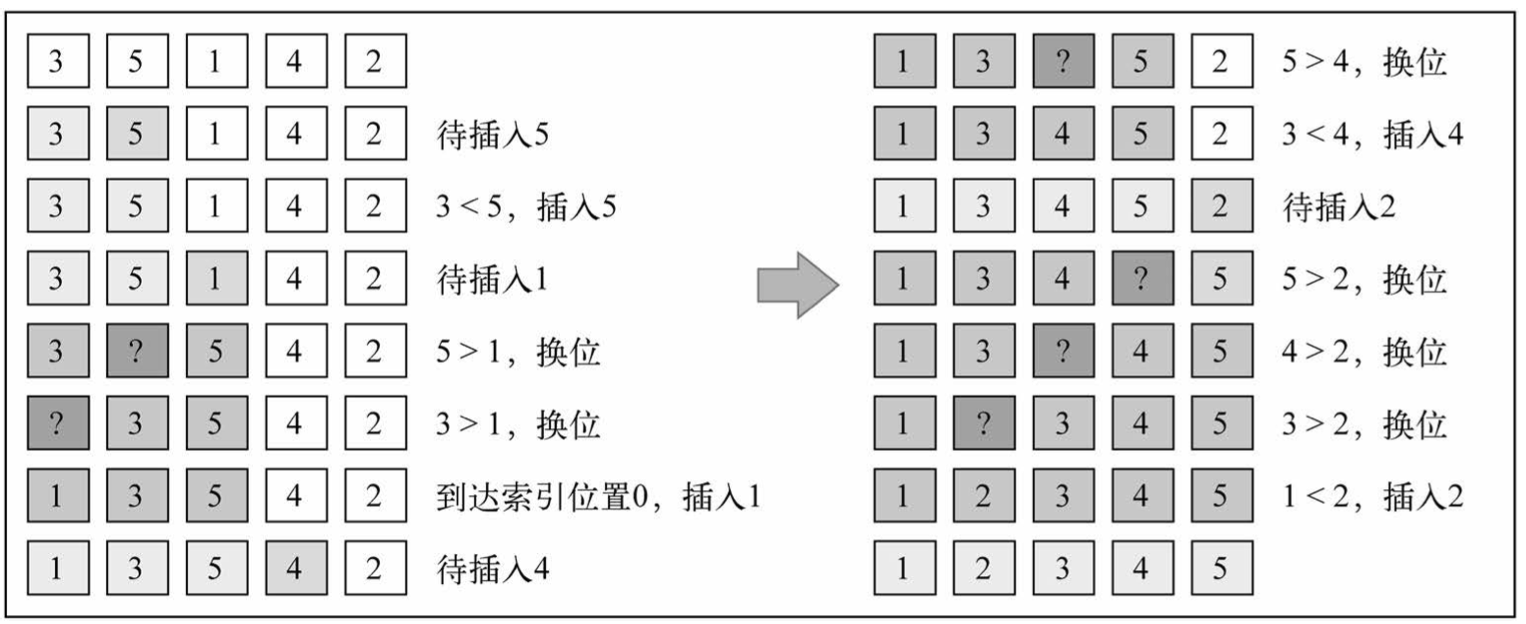
3、插入排序
插人排序每次排一个数组项,以此方式构建最后的排序数组。假定第一项已经排序了,接着, 它和第二项进行比较,第二项是应该待在原位还是插到第一项之前呢?这样,头两项就已正确排 序,接着和第三项比较(它是该插人到第一、第二还是第三的位置呢?),以此类推。
Array.prototype.insertSort = function () { for (let i = 1; i < this.length; i++) { let j = i let tmp = this[j] while (j > 0 && this[j-1] > tmp) { this[j]=this[j-1] j-- } this[j]=tmp } return this }
4、归并排序
归并排序是第一个可以被实际使用的排序算法。前三个排序算法性能不好,但归并排序性能不错,其复杂度为O(n log^n)。
JavaScript的Array类定义了一个sort函数Array.prototype.sort用以排序JavaScript数组(我们不必自己实现这个算法)。ECMAScript没有定义用哪个排序算法,所以浏览器厂商可以自行去实现算法。例如,Mozilla Firefox 使用归并排序作为Array.prototype.sort的实现,而Chrome使用了一个快速排序的变体。
归并排序是一种分治算法。其思想是将原始数组切分成较小的数组,直到每个小数组只有一 个位置,接着将小数组归并成较大的数组,直到最后只有一个排序完毕的大数组。
由于是分治法,归并排序也是递归的:
Array.prototype.mergeSort = function () { function merge(left, right) { let res = [] let indexL = 0 let indexR = 0 while (indexL < left.length && indexR < right.length) { if (left[indexL] > right[indexR]) { res.push(right[indexR]) indexR++ } else { res.push(left[indexL]) indexL++ } } while (indexR < right.length) { res.push(right[indexR]) indexR++ } while (indexL < left.length) { res.push(left[indexL]) indexL++ } return res } let apartArr = function (arr) { if (arr.length == 1) { return arr } let mid = Math.floor(arr.length / 2) let left = arr.slice(0, mid) let right = arr.slice(mid) return merge(apartArr(left),apartArr(right))//递归 } return apartArr(this) }
5)快速排序
快速排序也许是最常用的排序算法了。它的复杂度为O(nlog^n),且它的性能通常比其他的复杂度为O(nlog^n)的排序算法要好。和归并排序一样,快速排序也使用分治的方法,将原始数组分为较小的数组(但它没有像归并排序那样将它们分割开)。
快速排序的基本过程:
- 首先,从数组中选择中间一项作为主元
- 创建两个指针,左边一个指向数组第一个项,右边一个指向数组最后一个项。移动左指 针直到我们找到一个比主元大的元素,接着,移动右指针直到找到一个比主元小的元素,然后交 换它们,重复这个过程,直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元之 前,而比主元大的值都排在主元之后。这一步叫作划分操作。
- 接着,算法对划分后的小数组(较主元小的值组成的子数组,以及较主元大的值组成的 子数组)重复之前的两个步骤,直至数组已完全排序。
Array.prototype.quickSort = function() { const partition = (array, left, right) => { var pivot = array[Math.floor((right + left) / 2)] let i = left let j = right while (i <= j) { while (array[i] < pivot) { i++ } while (array[j] > pivot) { j-- } if (i <= j) { let aux = array[i] array[i] = array[j] array[j] = aux i++ j-- } } return i } const quick = (array, left, right) => { let index if (array.length > 1) { index = partition(array, left, right) if (left < index - 1) { quick(array, left, index - 1) } if (index < right) { quick(array, index, right) } } } quick(this, 0, this.length - 1) return this }