高级数据结构 | 二叉树遍历 —递归与非递归实现：先序、中序、后序遍历二叉树 ...

递归遍历二叉树

/* 先序遍历 */
void PreOrder(struct BtNode* p)
{
	if (NULL != p)
	{
		printf("%c ", p->data);
		PreOrder(p->leftchild);
		PreOrder(p->rightchild);
	}
}
/* 中序遍历 */
void InOrder(struct BtNode* p)
{
	if (NULL != p)
	{
		InOrder(p->leftchild);
		printf("%c ", p->data);
		InOrder(p->rightchild);
	}
}
/* 后序遍历 */
void PastOrder(struct BtNode* p)
{
	if (NULL != p)
	{
		PastOrder(p->leftchild);
		PastOrder(p->rightchild);
		printf("%c ", p->data);
	}
}

非递归

对于非递归的二叉树的遍历，可以看做是对栈的一种应用。其中对先序和中序的遍历是相同的，只是对获取到的结点数值输出顺序上有些略微不同罢了。而对于后序遍历，也只需要进行一些小的改动即可。

分析对于先序和中序的便利过程：

1. 对于一个二叉树，我们在遍历它的左孩子时，可以把左孩子当做一个新的二叉树根结点继续向下遍历。而停止的条件就是找到叶子结点，也就是说该结点没有左右孩子，度为0 。

2. 此时，我们利用栈回退至上层父结点，试图访问父结点的右孩子。如果该右孩子存在，那我们把该右孩子当做新的二叉树根结点向下遍历。如果该右孩子不存在，那么我们继续回退至再上一层，重复判断操作。

3. 最后，不论是先序还是中序，在访问最后一个结点时都是也只能是二叉树最右边的叶子结点。并且，我们从左子树向上回退时进行了“根”的出栈操作。也就是说，在遍历右子树时，该右子树的根结点已经不再栈中。结合以上两点，在遍历完所有结点时，退出的条件应为 栈为空 && 结点度为0 。

下图为从根结点至最左边的叶子结点的一次遍历（图左），在遍历至叶子结点 C 的左孩子后发现为空结点（图左），后回退至父节点 C 试图访问右结点发现为空结点（图中），则回退至再上一层的 B 结点处，发现其有右孩子，将此右孩子当做新的二叉树根结点（图中）。最后重复上述步骤直至满足退出条件栈为空 && 结点度为0。

分析对于后序的便利过程：

后序遍历的顺序为，左、右、根。很明显，上面使用的方法不适用与后序遍历，因为在我们遍历至右结点时，根结点是没有保存的。在上述的算法中，我们采用的是先将根结点入栈，如果左孩子为空，指针回退（出栈）至父节点，继续操作右孩子。因此，我们无法绕过根结点对右孩子进行访问。

因此，我们需要改变出入栈的方式，使我们在遍历至右孩子时，栈中任然保留着父节点的信息。

重新设计出入栈的方式：

• 在出栈时，判断是否对该子树已完整遍历。也就是说在出栈时，判断该结点的右结点是否已经被遍历过。
  • 如果没有遍历过，则该次回退为左结点处回退，需要继续遍历右结点。那么该节点继续入栈，并且遍历其右子树。
  • 如果已经遍历过，则该次回退为右结点处回退，证明右子树已经被遍历完整。同时，左子树也已经遍历完整，可以输出根结点。
• 根据以上的分析，我们需要一个flg 标记某个结点的右孩子是否被访问过。
  • 标记的方式为，每次回退前，将当前的有效结点(不为NULL的结点) 保存。

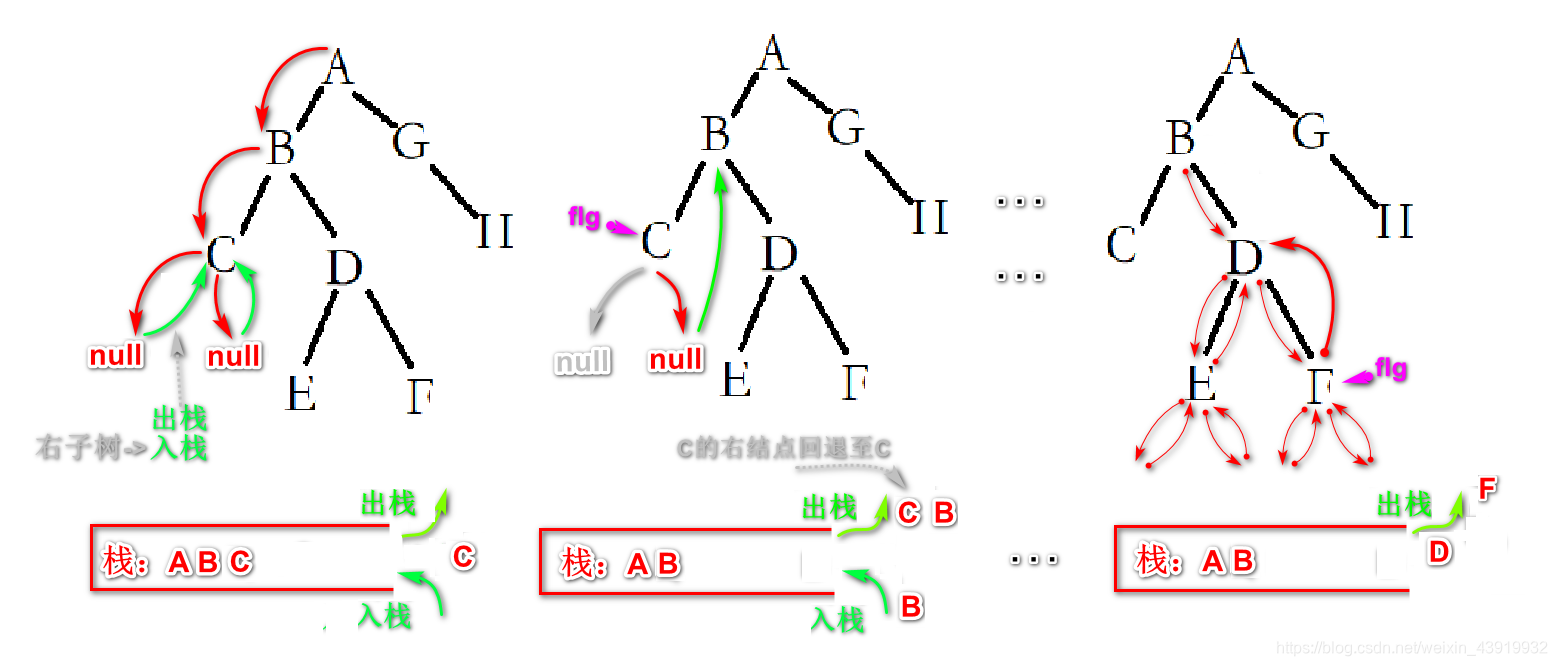
如下图所示，在 C 出栈时，发现C的右子树还没有遍历，则继续将C入栈（图左） 。直至发现 C 的左右子树都为空时，再次将 Ｃ 出栈回退至C结点处。此时C子树已经遍历完整，使用 flg 标记，再次回退至 B 结点处（图中）遍历右子树。 . . . 　. . .　 经过若干步后，如（图右）所示，在遍历完 F 结点后，将栈顶元素Ｄ出栈，回退至 D 结点处，而 F 结点已经遍历完整并且使用 flg 标记。
　　此时，对于D结点来说左右子树都遍历完整了。输出D结点的值后，我们继续使用 flg 标记D结点，而自身回退直B结点。对于B结点来说，左右子树都已经访问完，输出B结点后回退至A结点 。继续按此方法进行下去，直到我们到达 H 结点后依据栈中保留的信息逐步回退至根节点A处，而对于此时的A来说， 栈为空即是终止条件。

非递归先序遍历

void NicePreOrder(struct BtNode* p)
{
	if (NULL == p)	return;
	std::stack<struct BtNode*> st;
	while (!st.empty() || p != NULL)			// 最终的退出条件
	{
		while (p != NULL)						// 一直向左遍历左子树
		{
			st.push(p);
			std::cout << p->data << " ";		// 在遍历时，每一步访问的都是根，可以输出
			p = p->leftchild;
		}		/* while 解释  表示，此结点没有左孩子 */
		p = st.top();	st.pop();				// 回退至父节点
		p = p->rightchild;						// 试探右结点
	}
	std::cout << std::endl;
}

非递归中序遍历

void NiceInOrder(struct BtNode* p)
{
	if (NULL == p)	return;
	std::stack<struct BtNode*> st;
	while (!st.empty() || p != NULL)
	{
		while (p != NULL)
		{
			st.push(p);
			p = p->leftchild;
		}
		p = st.top();	st.pop();
		std::cout << p->data << " ";
		p = p->rightchild;	/* 碰到的叶子结点，回退父节点，右子树碰到叶子结点。
								这三步的顺序刚好是中序遍历的顺序 */
	}
	std::cout << std::endl;
}

非递归后序遍历

void NicePastOrder(struct BtNode* p)
{
	if (NULL == p)	return;
	std::stack<struct BtNode*> st;
	struct BtNode* flg = NULL;
	while (!st.empty() || p != NULL)
	{
		while (p != NULL)
		{
			st.push(p);
			p = p->leftchild;
		}

		p = st.top(); st.pop();

		if (p->rightchild == NULL || p->rightchild == flg)
		{
			std::cout << p->data << " ";	/* NULL输出叶子结点，falg是回退的根结点 */
			flg = p;		/* 回退前使用 flg 保存已遍历的结点信息 */
			p = NULL;		/* p置空，表明无左树可遍历，在下一轮的循环中直接进行出栈回退操作 */
		}
		else
		{
			st.push(p);		// 继续入栈
			p = p->rightchild;
		}
	}
	std::cout << std::endl;
}

测试输出

下面对比非递归与递归两种方式的输出结果。

int main()
{
	const char* str[] = {
			"ABC##DE##F##G#H##",
			"ABCDEFGH#########",
			"A#B#C#D#E#F#G#H##",
			"ABCD##EF##G#H####",
			"A#B#CDF###E##" };
	
	int i = sizeof(str)/sizeof(str[0]);
	while (i--)
	{
		const char* pstr = str[i];
		BinaryTree root = NULL;
		root = CreateTree1(&pstr);
		strPreOrder(root);	printf("
");
		std::cout << "---------------" << std::endl;

		/* 递归输出结果 */				/* 非递归输出结果 */
		PreOrder(root); printf("%*s	",i,"");		 NicePreOrder(root);
		InOrder(root);	printf("%*s	", i,"");		 NiceInOrder(root);
		PastOrder(root); printf("%*s	", i,"");		 NicePastOrder(root);


		std::cout << std::endl;
	}
	return 0;
}