【数学】分治 FFT

分治 FFT

模板题

为了方便阅读，我们将 \(f_n\) 记为 \(f(n)\)。

\(f\)​ 满足递推式 \(f(n) = \sum_{i=1}^n f(n-i)g(i)\)​，现在给你 \(n\)​ 还有 \(g(1),g(2)\dots g(n-1)\)​，求出 \(f(0),f(1)\dots f(n-1)\)​​，其中 \(f(0) = 1\)（首项）​。

原理

分治 + FFT。

重点讲解分治的过程。

我认为图示比较好理解（以 \(n=7\)​，求 \(f(n)\) 为例）：

可以发现 \(f(n)\) 是一个卷积的形式，在图中可以表述为：

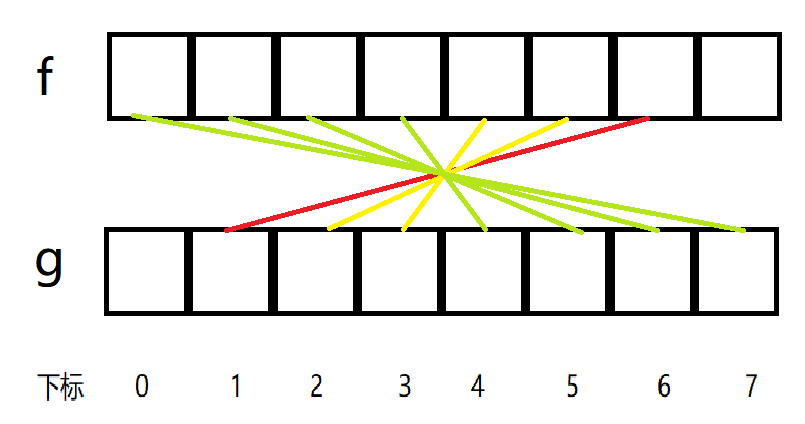
也就是红黄绿共七条线所对应的积的和。

我们可以利用分治分别将红、黄、绿对应的贡献加到 \(f(7)\) 上，这样就统计完了。

做法

• 利用分治先将左半段的 \(f\) 值处理出来。

• 然后让左半段的数组与 \(g\)​ 做 FFT，将贡献分别加到右半段对应的位置上。

结合代码理解：（因为这题取模，其实这是分治 NTT）

// Problem: P4721 【模板】分治 FFT
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4721
// Memory Limit: 125 MB
// Time Limit: 5000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using namespace std;

#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define dwn(i,a,b) for(int i=(a);i>=(b);i--)

using pii = pair<int, int>;
using ll = long long;

#define int long long

inline void read(int &x){
    int s=0; x=1;
    char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-')x=-1;ch=getchar();}
    while(ch>='0' && ch<='9') s=(s<<3)+(s<<1)+ch-'0',ch=getchar();
    x*=s;
}

/////////////////////////////////////////////////////////////////////

const int N=3e5+5, mod=998244353, rt=3;

ll fpow(ll x, int p, ll mod){
	int res=1;
	for(; p; p>>=1, x=x*x%mod) if(p&1) res=res*x%mod;
	return res;
}

ll inv(ll x, ll mod){
	return fpow(x, mod-2, mod);
}

int rev[N], tot=1, bit;

void NTT(ll *a, int type, int mod){
	for(int i=0; i<tot; i++){
		a[i]%=mod;
		if(i<rev[i]) swap(a[i], a[rev[i]]);
	}
	
	for(int mid=1; mid<tot; mid<<=1){
		ll w1=fpow(rt, (type==1? (mod-1)/(mid<<1): mod-1-(mod-1)/(mid<<1)), mod);
		for(int i=0; i<tot; i+=mid*2){
			ll wk=1;
			for(int j=0; j<mid; j++, wk=wk*w1%mod){
				auto x=a[i+j], y=wk*a[i+j+mid]%mod;
				a[i+j]=(x+y)%mod, a[i+j+mid]=(x-y+mod)%mod;
			}
		}
	}
	
	if(type==-1){
		for(int i=0; i<tot; i++) a[i]=a[i]*inv(tot, mod)%mod;
	}
}

int n;
int f[N], g[N];

int A[N], B[N];

void conv(int *A, int *B){
	NTT(A, 1, mod), NTT(B, 1, mod);
	rep(i,0,tot-1) (A[i]*=B[i])%=mod;
	NTT(A, -1, mod);
}

void divi(int l, int r){
	if(l>=r) return;
	int mid=l+r>>1;
	divi(l, mid);
	
	// init
	tot=1, bit=0;
	int len=r-l+1;
	while(tot<=len-2) bit++, tot<<=1;
	for(int i=0; i<tot; i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
	rep(i,0,tot-1) A[i]=B[i]=0;
	rep(i,l,mid) A[i-l]=f[i];
	rep(i,1,r-l) B[i-1]=g[i];
	
	conv(A, B);
	
	rep(i,mid+1,r) (f[i]+=A[i-l-1])%=mod;
	divi(mid+1, r);
}

signed main(){
	cin>>n; n--;
	f[0]=1;
	rep(i,1,n) read(g[i]);
	
	divi(0, n);
	
	rep(i,0,n) cout<<f[i]<<' ';
	cout<<endl; 
	return 0;
}