多项式学习笔记0

就最基础的3个多项式算法：FFT，NTT 和 拉格朗日插值

普通多项式乘法

FFT

把多项式用DFT转化成点值表示法，然后再用IDFT转化回来。

我们把多项式的项数写成2的幂次（不够就再补几位），DFT利用单位根的优良性质，有（直接写结论）

[A(x)=sum_{i=0}^{frac{n}{2}-1} a_{2i}x^i\ B(x)=sum_{i=0}^{frac{n}{2}-1} a_{2i+1}x^i\ F(omega_n^{k})=A(omega_{n/2}^k)+omega_{n}^{k}B(omega_{frac{n}{2}}^k)\ F(omega_n^{k+frac{n}{2}})=A(omega_{n/2}^k)-omega_{n}^{k}B(omega_{frac{n}{2}}^k) ]

可以递归求解。然后 IDFT 的时候把 (omega_{n}^{k}) 换成 (omega{n}^{-k}) 即可。最终的答案要除以 (n)。

考虑优化用递推优化常数。

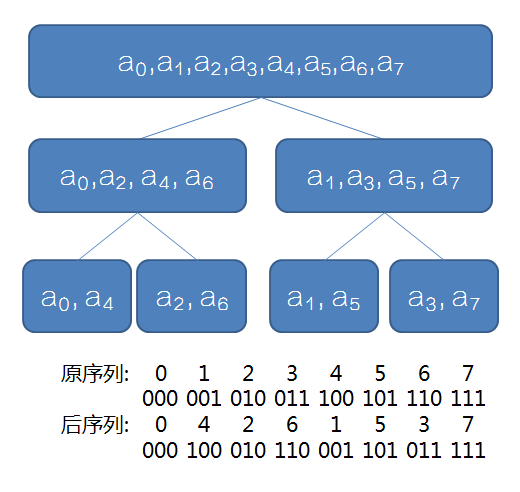
如上是FFT的递归树。观察到底下的所有数的排列时候特征的（二进制位等于其原下标的反转），考虑从下向上递推计算。

其中对于每个数的二进制反转，可以递推 rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1))，其中 l 为 (n) 的位数。

具体算法步骤

for 每一层（记录长度len）
      for 每一块(i)
            for 每一个单位根（ω_j）
                  x=a[i+j], y=ω*a[i+j+len]
                  a[i+j]=x+y, a[i+j+len]=x-y

#include<bits/stdc++.h>
#define rep(i,a,b) for(register int i=(a);i<=(b);i++)
#define per(i,a,b) for(register int i=(a);i>=(b);i--)
using namespace std;
const int N=3e6+9;
const double pi=acos(-1);

inline int read() {
    register int x=0, f=1; register char c=getchar();
    while(c<'0'||c>'9') {if(c=='-') f=-1; c=getchar();}
    while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+c-48,c=getchar();}
    return x*f;
}

struct cp {
	double x,y;
	cp(double xx=0,double yy=0) {x=xx,y=yy;}
};
cp operator + (cp a,cp b) {return cp(a.x+b.x,a.y+b.y);}
cp operator - (cp a,cp b) {return cp(a.x-b.x,a.y-b.y);}
cp operator * (cp a,cp b) {return cp(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

int n,m,l,lim,r[N];
cp f[N],g[N];

void fft(cp *a,int t) {
	rep(i,0,lim-1) if(i<r[i]) swap(a[i],a[r[i]]);
	for(int len=1;len<lim;len<<=1) {
		cp dw(cos(pi/len),t*sin(pi/len));
		for(int i=0;i<lim;i+=(len<<1)) {
			cp w(1,0);
			for(int j=0;j<len;j++,w=w*dw) {
				cp x=a[i+j],y=w*a[i+j+len];
				a[i+j]=x+y,a[i+j+len]=x-y;
			}
		}
	}
}

int main() {
	n=read(), m=read();
	rep(i,0,n) f[i].x=read();
	rep(i,0,m) g[i].x=read();
	for(lim=1;lim<=n+m;l++,lim<<=1);
	rep(i,0,lim-1) r[i]=(r[i>>1]>>1)|((i&1)<<l-1);
	fft(f,1), fft(g,1);
	rep(i,0,lim) f[i]=f[i]*g[i];
	fft(f,-1);
	rep(i,0,n+m) printf("%d ",(int)(0.5+f[i].x/lim));
	return 0;
}

NTT

用原根 (g) 代替 (omega)。(omega_n o g^{frac{p-1}{n}})，(omega_{n}^{k} o g^{frac{p-1}{n} imes k})。逆变换的时候 (g o g^{-1}) 就行了。

常用的 NTT 模数：(998244353, 1004535809, 469762049)，原根都是 (3)。

#include<bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(register int i=(a);i<=(b);i++)
#define per(i,a,b) for(register int i=(a);i>=(b);i--)
using namespace std;
const int N=3e6+9,gg=3,mod=998244353,ig=332748118;

inline int read() {
    register int x=0, f=1; register char c=getchar();
    while(c<'0'||c>'9') {if(c=='-') f=-1; c=getchar();}
    while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+c-48,c=getchar();}
    return x*f;
}

int n,m,f[N],g[N],l,lim,r[N];

int ksm(int x,int y,int res=1) {
	while(y) {
		if(y&1) res=res*x%mod;
		y>>=1, x=x*x%mod;
	}
	return res;
}

int add(int x,int y) {x+=y; return x>=mod?x-mod:x;}
int mns(int x,int y) {x-=y; return x<0?x+mod:x;}

void ntt(int *a,int t) {
	rep(i,0,lim-1) if(i<r[i]) swap(a[i],a[r[i]]);
	for(int len=1;len<lim;len<<=1) {
		int dg=ksm((t>0?gg:ig),(mod-1)/(len*2));
		for(int i=0;i<lim;i+=(len<<1)) {
			int w=1;
			for(int j=0;j<len;j++,w=w*dg%mod) {
				int x=a[i+j],y=w*a[i+j+len]%mod;
				a[i+j]=add(x,y), a[i+j+len]=mns(x,y);
			}
		}
	}
}

signed main() {
	n=read(), m=read();
	rep(i,0,n) f[i]=read();
	rep(i,0,m) g[i]=read();
	for(lim=1;lim<=n+m;l++,lim<<=1);
	rep(i,0,lim) r[i]=(r[i>>1]>>1)|((i&1)<<l-1);
	ntt(f,1), ntt(g,1);
	rep(i,0,lim) f[i]=f[i]*g[i]%mod;
	ntt(f,-1);
	rep(i,0,n+m) printf("%lld ",(f[i]+mod)*ksm(lim,mod-2)%mod);
	return 0;
}

P3338 [ZJOI2014]力

[egin{aligned} E_i&=frac{F_i}{q_i}\ &= sum_{j=0}^{i} frac{q_j}{(i-j)^2} - sum_{j=i}^{n} frac{q_j}{(j-i)^2}\ end{aligned} ]

我们发现左边是一个卷积形式。然后左右两边分开讨论。令 (E_i=L_i-R_i)。令 (g_i=frac{1}{i^2})。

[egin{aligned} L_i&= sum_{j=0}^{i} q_j g_{i-j}\ R_i&= sum_{j=i}^{n} q_j g_{j-i}\ &= sum_{j=0}^{n-i} q_{j+i} g_{j} end{aligned} ]

一个trick，将 q 反转。设 (p_i=q_{n-i})，则有

[R_i=sum_{j=0}^{n-i} q_{n-i-j} g_{j} ]

是卷积形式。设 (R_{i}=S_{n-i})，则有

[egin{aligned} L(x)&=Q(x) imes G(x)\ S(x)&=P(x) imes G(x)\ E_i&=l_i-s_{n-i} end{aligned} ]

code: https://www.luogu.com.cn/record/46475365

P4173 残缺的字符串

对于串 (a[0dots m-1]) 和串 (b[0dots m-1])，如果要求匹配，则有

[sum_{i=0}^{m-1} a_ib_i(a_i-b_i)^2=0 ]

考虑带入式子。设 (f_x) 表示最终以第 (x) 位结尾的答案。设 (a) 为反转后的 (a)，则有

[egin{aligned} f_x &= sum_{i=0}^{m-1} a_i b_{x-i} (a_i-b_{x-i})^2\ &= (sum_{i=0}^{m-1} a_i^3 b_{x-i}) - (2sum_{i=1}^{m} a_i^2 b_{x-i}^2) +(sum_{i=0}^{m-1} a_{i}b_{x-i}^3)\ end{aligned} ]

记 (A_p(x)=sum a^p_ix^i, B_p(x)=sum b_ix^{i}, C(x)=sum f_ix^i)，则有

[C=A_3 imes B_1-2A_2 imes B_2+A_1 imes B_3 ]

做 3 次多项式乘法即可。

https://www.luogu.com.cn/record/47534859

拉格朗日插值

普通的拉格朗日插值

给出一个多项式的点值表示法，然后希望能在 (O(n^2)) 的时间内进行插值（即计算出这个多项式）

用高斯消元可以 (O(n^3)) 求解（待定系数法）

拉格朗日插值定理说，设点对为 ((x_i,y_i))，那么多项式为

[f(x)=sum_{i=0}^{n} y_iprod_{i eq j} frac{x-x_j}{x_i-x_j} ]

很妙！!1

洛谷模板 code: https://www.luogu.com.cn/record/46488893

重心拉格朗日插值法

可以动态 (O(n)) 时间加入一个新的点。具体做法就是把第 (i) 个点得贡献提取出来，做到能在新进来一个点时 (O(1)) 增量求出。

[egin{aligned} f(x)&=sum_{i=0}^{n}y_iprod_{i eq j} frac{x-x_j}{x_i-x_j}\ &=(prod_{i=0}^{n} x-x_i) imes sum_{i=0}^{n} prod_{i eq j} frac{y_i}{(x-x_i)(x_i-x_j)}\ end{aligned} ]

维护 (w_i=prod_{i eq j} frac{y_i}{(x_i-x_j)}) 这样每个部分就都能增量求解了。

LOJ模板

code: https://loj.ac/s/1063338

CF622F The Sum of the k-th Powers

求 (sum_{i=0}^{k} i^k)。

有一个简单的小性质，对于一个通项为 (k) 次多项式 (f(x)) 的序列，差分的通项 (g(x)) 是一个 (k-1) 次整式。其逆定理同样适用。考虑 (a_i=sum_{j=1}^{n} i^k) 的差分序列 (a_i=i^k)，其通项 (g(x)=x^k) 显然是一个 (k) 次整式。那么我们知道原序列 (a) 的通项 (f(x)) 为一个 (k+1) 次多项式。 我们考虑用拉插来求出这个多项式。由于 (k) 很小，我们插 (k+2) 组 ((i,a_i)) 即可得到这个通项。为了方便，我们选择 (i=1,2,...,n+2)，这样可以 (O(k)) 处理出 (a_i) 然后由于插值连续，拉插可以做到 (O(k))。

取值连续的拉插优化：

[f(x)=sum_{i=1}^{k+2} a_iprod_{i eq j} frac{n-j}{i-j}\ ]

我们设关于 (n-j) 的前后缀积 (p_i=prod_{j=1}^{i}n-j)，(s_i=prod_{j=i}^{k+2}n-j)。

[f(x)=sum_{i=1}^{k+2} a_i frac{p_{i-1}s_{i+1}}{(-1)^{k+2-i}(i-1)!(k+2-i)!} ]

预处理出 (p,s) 和阶乘逆元，然后线性筛求 (i^k)，可以做到 (O(k))。但是我懒，所以在处理 (a) 时就不筛了。

code: https://codeforces.com/contest/622/submission/107185130

P4593 [TJOI2018]教科书般的亵渎

考虑把所有怪物的血量画成一张柱形图拼起来。我们发现每一张亵渎等于说消掉一个梯形。再随便玩玩可以发现一共要使用 (m+1) 张亵渎。我们枚举每一张亵渎的使用。

易推除式子

[ans=sum_{i=0}^{m} sum_{j=1}^{n-a_i} j^{m+1} - sum_{i=0}^{m-1} sum_{j=i+1}^{m} (a_j-a_i)^{m+1} ]

前半部分式子用拉插，后半部分暴力算，(O(m^2))。

code: https://www.luogu.com.cn/record/46532239

CF995F Cowmpany Cowmpensation

插值优化 DP。

考虑设计 (dp) 方程 (f(u,i)) 表示 (u) 子树且 (u) 的值为 (i) 的方案数。考虑前缀和优化，(g(u,i)) 为 (sum_{j=1}^{i} f(u,i))，则有

[f(u,i)=prod g(v,j) ]

观察合并的过程，我们发现 (g) 为 (f) 的部分和，然后 (f) 为 (g) 的乘积。所以 (g) 是一个多项式！考虑证明。(f(leaf,*)) 是一个 (0) 次式。然后 (g(x,i)) 是在 (i) 处的点值，转移相当于点值表达式相乘，即多项式的乘法，乘出来是一个 (f) 为 (sz_x-1) 次多项式。所以我们计算出 满足 (xle n) 的 (g(1,x)) 然后插值即可。复杂度 (O(n^2))。

code: https://codeforces.com/contest/995/submission/107289330