上下文无关文法

下面给出一个例子:

上下文无关文法的推导


生成树

下面给出一个例子:

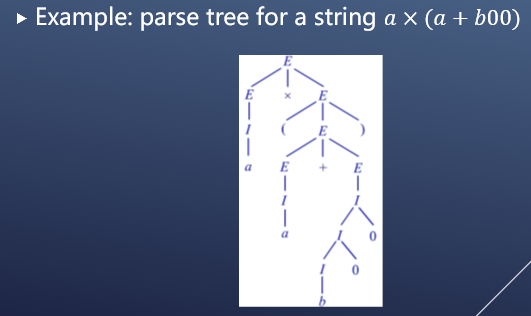
歧义文法
如果一个字符串有多个推导,或者有多个生成树可以生成同样的字符串,则称这个文法是歧义的。如果每个字符串都只对应于一个生成树,则称这个文法是非歧义的。
下面给出一个例子:

去除文法的歧义性
无法根据一个确切的算法来判断一个文法是否是歧义的,而且如果一个上下文无关的语言只存在一个具有歧义的文法,那么就无法去除歧义性。
出现歧义的原因:
- 没有考虑运算符的优先级。例如上面的例子,左图是×先于+结合,而右图是+先于×结合,这两者都是正确的生成树。然而在一个无歧义的文法中只允许左图的结构。
- 一系列同样的运算符既可以从左到右也可以从右到左结合。例如对于字符串E+E+E将会得到两颗不同的生成树,因为加法满足结合律,所以无论从左还是从右结合都无所谓,但是为了去除歧义,习惯性的采用从左到右的结合方式。
对于一个问题,强制优先级的问题的解决方法是引入几个不同的变元,每个变元代表拥有同样级别的“黏结强度”的那些表达式。对于上面那个具有歧义的文法,可以进行如下转化:

最左推导作为一种歧义的表达
即使文法的是无歧义的,推导也有可能不唯一。但下面的结论总是成立的:在无歧义的文法中,最左推导是唯一的,最右推导也是唯一的。对于任何文法G=(V, T, P, S)和T*中的串w,w有两颗不同的生成树当且仅当从S到w有两个不同的最左推导。
固有的歧义性
如果一个上下文无关的语言L的所有的文法都是歧义的,则称它是固有歧义的。只要L有一个文法是非歧义的,那么L就是非歧义的。例如,在上面的例子中的文法所生成的语言实际上是非歧义的,因为它存在一个非歧义的文法。