密码学基础(五)

哈希函数

摘要性：在最基本的层面上，一个哈希函数需要将输入的一个长的信息映射到一个较短的信息上。

碰撞性：即两个不同的输入映射到同一个摘要上。如果两个不同的输入 x 和 x‘ 有H(x)=H(x')，则称 x 和 x’ 发生了碰撞。

抗碰撞性：如果对于任何一个PPT上的敌手找到一个碰撞是无法实现的，则称这个函数具有抗碰撞性。

通常讨论抗碰撞性都是在函数定义域大于值域的情况下的，这种情况下碰撞必然是存在的，但是一般很难以找到碰撞。

哈希函数的定义：一个哈希函数(输出长度为 l )由两个PPT上的算法(Gen, H)构成

• Gen：一个概率算法，以一个安全参数1ⁿ作为输入，然后输出密钥 s ，假设安全参数 1ⁿ 隐含在s中。
• H：将一个密钥 s 以及一个01串 x ∈{0, 1}*作为输入，然后输出H^s(x)∈{0, 1}^l(n)，其中的 n 是隐含在 s 中的安全参数。

如果 H 是定义在输入固定为 x∈{0, 1}^l'(n)并且l'(n)>l(n)，则称这种哈希函数是一个固定长度的哈希函数，并且称算法 H 为压缩函数。

这了需要注意的是哈希函数中的密钥与普通对称加密方案中的密钥的区别：

1. 并不需要保证所有的输入都能映射到一个有效的输出(比如某些哈希函数是定义在一个确定的密钥 s 上的)，并且因此 s 由算法Gen生成，而不是像加密算法中那样随机的选择。
2. 哈希函数中的密钥并不需要保证其机密性，而且当讨论一个哈希函数的抗碰撞性时是保证敌手在获取了密钥后还是无法找一对碰撞。

抗碰撞性：如果一个PPT上的敌手找到一对碰撞的概率小于某个可忽略函数则称这种哈希函数是具有抗碰撞性的。

不带密钥的哈希函数：在实际应用中使用的密码哈希函数通常都是有一个固定的输出长度，并且是不带密钥的(也就是说哈希函数只有一个固定的函数H:{0,1}*→{0,1}l(n))。而算法中总是有一个输出碰撞的常量时间算法，用于输出硬编码到算法本身的一对碰撞。一般来说，碰撞对都是未知的并且计算上很难找到的。

哈希函数的安全性：

抗第二原像：给定一个 s 以及一个随机的 x ，对于一个PPT上的敌手计算上很难求出 x' ≠ x 满足H^s(x')=H^s(x)。

抗原像：给定一个 s 以及一个随机的 y ，对于一个PPT上的敌手计算上很难求出一个满足H^s(x)=y的 x 值。

破解的难度：抗原像 > 抗第二原像 > 抗碰撞

哈希函数定义域扩展

Merkle-Damgard转换是一种常见的用于扩展哈希函数定义域的方法，用于将压缩函数扩展为成能够满足需求的哈希函数，并且同时保持前者的抗碰撞特性。

因此在设计抗碰撞的哈希函数的时候，一般都着重设计固定长度的哈希函数，也就是说压缩一个比特的输入与压缩任意长度的输入的难易程度是相同的。

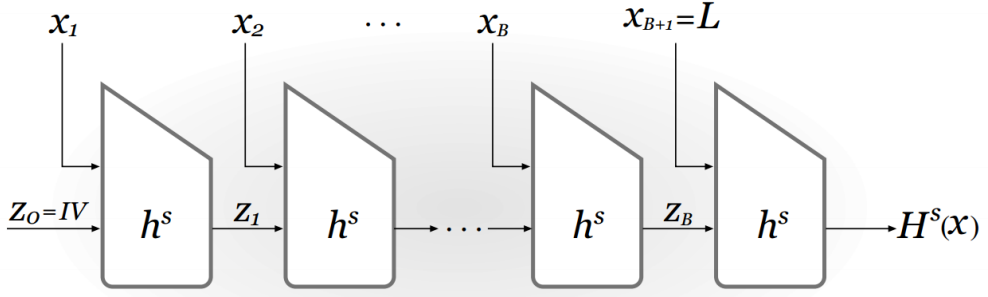
Merkle-Damgard转换：设(Gen, h)是一个固定长度的哈希函数，其输入长度为 2n 而输出长度为 n，则可以构造一个哈希函数：

• Gen：不变
• H：对于一个输入密钥 s 以及一个01串 x∈{0, 1}*，x的长度 L 小于2ⁿ，则：

1. 设B := ceil( L/n ) ，其实B就是分组的个数，在x末尾填充0使 L 为n的倍数，然后将 x 分成 B 份长度为 n 的分组x₁, x₂, ..., x_B。然后设x_B+1 := L，其中 L 被编码成 n 比特的01串。
2. 设z₀ := 0ⁿ (z₀也被称为初始向量)，初始向量是任意的，并且可以被替换成其他任何一个常量。
3. 对 i = 1, 2, ..., B+1，计算z_i := h^s(z_i-1||x_i)
4. 最后输出z_B+1

其实意图如下：

定理：如果(Gen, h)是抗碰撞的，那么(Gen, H)也是抗碰撞的

证明.

设 x 和 x‘ 是两个不同的输入，它们的长度分别为L和L'，则可以证明对于任意的密钥 s ，在H^s中的碰撞都能找到h^s中的碰撞。

令，H^s(x) = H^s(x')

设x₁, ..., x_B是 x 的分组，x'₁, ..., x'_B'是 x’ 的分组，则有两种情况：

L≠L' ：H^s(x) = z_B+1 = h^s(z_B||L), H^s(x') = z'_B'+1 = hs(z'_B'||L') 

因为H^s(x) = H^s(x')，所以h^s(z_B||L) = hs(z'_B'||L')，而L≠L'，所以z_B||L和z'_B'||L'必然是两个不同的输入，而这就是hs中的一对碰撞。

L=L‘：则B=B'

设 T_i = z_i-1||x_i，即h^s的第 i 次输入，令T_B+2=z_B+1；同样的定义T'₁, ..., T'_B+2为计算Hs(x')过程中每次h^s的输入。

设N是满足T_N≠T'_N的最大值，因为 x≠x’，而L=L‘，所以N必然是存在的。

因为T_B+2 = z_B+1 = H^s(x) = H^s(x') = z'_B+1 = T'_B+2，所以N≤B+1。

当N=B+1时，h^s(T_N) = z_B+1 = H^s(x) = H^s(x') = z'_B+1 = h^s(T'_N)，则因为T_N≠T'_N，所以T_N和T'_N是h^s中的一对碰撞。

用哈希函数验证任意长度消息完整性

在前面构造任意长度的MAC时，讲述了两种方法，一种是常规的构造方法，第二种是基于为随机函数的CBC-MAC。而这里介绍的hash-and-MAC，是另一种一种基于抗碰撞哈希函数的方法。

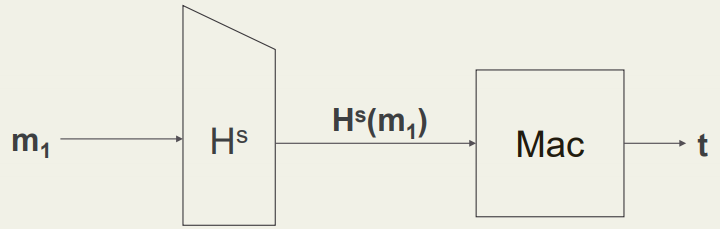
Hash-and-MAC构造方法：设Π=(Mac, Vrfy)是一个对于输入长度为l(n)的消息验证码，设Π_H=(Gen_H, H)是一个输出长度为 l(n) 的哈希函数

• Gen'：对于输入的安全参数1ⁿ，随机的选择 k∈{0, 1}ⁿ，然后运行Gen_H(1ⁿ)来获取s，最终输出k' := <k, s>
• Mac'：对于输入的密钥<k, s>以及一个任意长度的消息m∈{0, 1}*，输出 t ← Mac_k(H^s(m))
• Vrfy'：对于输入的密钥<k, s>以及一个任意长度的消息m∈{0, 1}*，以及一个MAC标签 t ，当且仅当Vrfy_k(H^s(m),t)=1的情况下才输出 1。

Hash-and-MAC的示意图如下：

定理：如果Π是一个对于长度为 l 的消息安全的MAC，ΠH是一个抗碰撞的哈希函数，则HMAC也是一个对任意长度消息安全的MAC。

证明.

hash-and-MAC的一种特定的实例被称为HMAC

HMAC的构造方法：设(GenH, H)是一个由(GenH, h)经过Merkel-Damgrad转换而来的对于长度为n+n'输入的哈希函数。设ipad和opad是两个固定常量

• Gen：对于输入1n，运行GenH(1n)来获取密钥s，然后k∈{0, 1}n'，最后输出密钥<s, k>
• Mac：对于输入的密钥<s, k>以及一个消息m∈{0, 1}*，输出t := H^s( (k⊕opad) || H^s(k⊕ipad)||m )
• Vrfy：对于输入的密钥<s, k>以及一个消息m∈{0, 1}*，以及一个MAC标签 t ，当且仅当 t = H^s( (k⊕opad) || H^s(k⊕ipad)||m )的时候才输出1。

HMAC是一种工业标准并且在实际中得到了广泛的应用。它是高效且易于实现的，并且由一个基于对实际哈希函数的假设的安全性的证明来支持其安全性。

哈希函数的输出长度下限

对于哈希函数的某些攻击方式的存在，意味着哈希函数H的输出长度存在着一个下限从而保证其安全性。

寻找碰撞的生日攻击(Birthday attack)：

设H: {0, 1}*→{0, 1}^l是一个哈希函数

一个普通的在O(2^l)时间内寻找碰撞的方式：直接计算对于H的2^l+1个不同的输入所产生的输出，因为输出的长度为l，那么必然能够找到一个碰撞。

对上面个的那种寻找碰撞的方法进行归纳，可以选择 q 个不同的x₁, ..., x_q，计算y_i := H(x_i)，然后检查y_i中是否存在两个相等的值。为了分析当q＜2^l时找到碰撞的概率，可以将H看作一个伪随机函数。

那么对于每个 i ，假设y_i = H(x_i)在{0, 1}^l中均匀分布，并且每个y_i的取值都相互独立。则问题就转变成：

在y₁, ..., y_q在{0, 1}^l中均匀分布，则i ≠ j，y_i = y_j的概率是多大？

这个问题就是所谓的生日问题(Birthday Problem)：假设有q个人在同一个房间内，那么他们中有两个人的生日在同一天的概率为多大？（假设一年365天）

数学研究结果是：如果y₁, ..., y_q的取值是在{1, ..., N}之间均匀选择的，那么当q=Θ(N^1/2)的时候碰撞的概率大约为1/2。所以在生日问题中，如果房间里的人有23人，那么碰撞的概率就大于1/2。

从上面的问题可以看出：对于一个运行在时间T内的抗碰撞的哈希函数，假设每求一次H的值所花费的时间是一个单位时间，那么这个哈希函数的输出长度至少为2logT比特，因为2^2logT/2=T。

这里需要注意几个点：

1. 哈希函数的输出长度足够长只是哈希函数安全的一个必要条件而非充分条件
2. 生日攻击只是用来寻找碰撞的
3. 如果规定哈希函数的求H的次数必须小于2^l，那么就不存在某种针对哈希函数的抗第二原像以及抗原像的攻击方式

随机预言机模型

随机预言机模型假设存在一个公共的随机的函数H，可以通过输入 x 向 H 查询 H(x) 的值。

为了区别，将前面所使用的模型（没有随机预言机的模型）称为标准模型

在实际中并没有随机预言机的存在，不过有人建议使用公开的可信任的服务器来充当随机预言机

随机预言机模型提供了一种可用于设计和验证密码方案的形式化方法。

“预言机”：就是一个简单的黑盒，将一个二进制串作为输入，然后输出另一个二进制串。而且这个黑盒的内部构造是未知且难以捉摸的。每一个通信方或者敌手都可以与这个黑盒进行交互（查询）。

向预言机的查询被认为是私密的。也就是说如果某人向预言机查询 x 对应的输出，那么没有其他的人知道这个 x ，甚至没人知道这个人向预言机进行了查询。

预言机的一致性：如果预言机输入 x 对应的输出是 y ，那么无论查询多少次，x 对应的输出都应该是  y。

两种构造随机预言机的方法：

• 在一个从某个确定定义域到值域的所有函数集合中概率均匀的选择一个函数
• 将预言机 H 想象成一张表，初始时这张表是空白的，当有人向预言机查询 x_i 对应的输出时，预言机检查(x_i, y_i)是否在这张表上：如果有，那么输出y_i；如果没有，那么随机生成一个长度为l(n)的二进制串 y ，然后将这个y作为输出，并令y_i=y，将(x_i, y_i)填写到表格中。

随机预言机模型的属性：

1. 如果H(x)没有被查询过，那么H(x)的值就是随机的。也就是说随机预言机 H 是一个真正的随机数生成器，比PRG更强的随机发生器。
2. 当A向仿真器查询 x 时，仿真器可以看到这个 x 以及H(x)。这个属性并不与前面所提到的随即预言机的私密性相矛盾，因为这个属性只有在一个仿真器利用 A 作为自己的子程序的随机预言机模型中才成立。
3. 仿真器可以按照自己的选择将 H(x) 作为 A 查询 x 的结果。

随机预言机的简单说明：假设随机预言机是一个将lin输入映射lout输出的函数，其中l_in, l_out > n，n是安全参数

• 利用随机预言机构造伪随机生成器：当l_out > l_in时，可以直接将RO作为一个伪随机生成器
• 利用随机预言机构造抗碰撞哈希函数：当l_out < l_in时，可以直接将RO作为一个抗碰撞的哈希函数
• 从随机预言机构造伪随机函数：当l_in(n) = 2n, l_out(n) = n 时，可以定义一个伪随机函数：F_k(x) = H(k||x)，其中|k| = |x| = n

哈希函数的运用

指纹与去重

但是用一个抗碰撞的哈希函数时，一个文件的哈希值可以充当该文件的标识符

换句话说 H(x) 对于文件 x 来说相当于x文件的指纹，所以可以通过检查两个文件的哈希值来确定两个文件是否相等。

病毒指纹：病毒扫描器用于标识病毒然后阻止或者进行隔离。其中最重要的一个步骤就是将所有已知的病毒的哈希值存储在一个服务器的数据库中，然后每当下载一个应用或者接受一封邮件的时候就将其哈希值与数据库中的哈希值进行比对。

去重复：在云存储中，多个用户将他们的数据云存储服务器上，如果有多个用户存储了同样的一个文件，那么云存储服务器只需要存储一次就可以满足需求。为了实现这个目标，每当用户上传文件的时候需要先上传文件的哈希值，如果哈希值已经存储在云端，那么云存储服务器只需要简单的添加一个在那个文件上的指针来表示该用户也存储了该文件。

P2P文件共享：在P2P文件共享系统中，服务器维持一个表来提供文件查找的功能，这些表中存储着已有的文件的哈希值，而这些哈希值也相当于唯一的标识了每个文件，并且并不会占用太多的空间。

默克尔树

假设某个用户向服务器上传多个文件x₁, ..., x_t，然后当用户取回某个文件x_i时，他希望这个文件是最初上传的那个文件并且没有被更改过。

在本地上为每个文件独立的存储一个哈希值h₁, ..., h_t，当取回文件x_i的时候，只需要检查H(x_i)是否等于h_i即可。然而这样做的话，本地的存储成本会随着 t 的增大而线形增大。

另一种方法是计算h := H(x₁, ..., x_t)，然后只在本地上存储 h 的值。然而这样做的话，用户取回xi文件后想要检查其完整性就需要取回所有的文件，这样显然会使效率变低。

现在最常用的方式是默克尔树。

下面是一个默克尔树的实例：

输入的多个文件x₁, ..., x₈，分别计算出H(x₁, x₂), ..., H(x7, x8)，然后将H(x1, x2)与H(x3, x4)进行异或得到h1...4，同样的方法得到h5...8，然后再将h1...4与h5...8进行异或得到h1...8。

事实上，默克尔树也提供了一种不同于前面所说的Merkel-Damgard转换的哈希函数定义域的扩展方式，并且通常用MT表示由默克尔树方式转换而来的扩展定义域的哈希函数。

定理：如果哈希函数MT是由抗碰撞的固定长度哈希函数H经过默克尔树扩展而来的，那么MT也是抗碰撞的。

回到最开始的那个问题，默克尔树也提供了一种在O(log t)次交互内完成前面所说的问题的高效率解决方案。

用户计算h := MT(x1, ..., x8)，并且将 h 的值存储到本地。

比如用户需要取回文件x3，那么服务器需要将x4，H(x1, x2)，h(5, ..., 8) 一并返回给用户，然后用户用MT的算法计算出h‘，然后将h’与存储在本地上的h进行比对即可完成文件的完整性检验。

密钥哈希

假设一个用户在使用他的电脑前需要输入一个密钥，那么为了进行验证，密钥必须以某种形式存储在电脑的某个位置。如果这个密钥是直接以明文的形式存储在电脑上，那么如果某个敌手在偷到了这台电脑后可以直接从硬盘上读取这个密钥，然后成功的作为用户进行登录。

可以存储密钥的哈希值代替密钥的明文，从而避免这种风险。

在硬盘上存储 hpw = H(pw)，每当用户输入 pw‘ 进行登录时，验证H(pw')是否等于hpw。

但是如果密钥是从一个比较小的空间里面选取的，那么敌手在从硬盘上读取了hpw后可以一次遍历每个可能的取值并进行验证，知道验证通过。

此外，哈希函数的抗原像的安全性质在这里也并不能提供充分的安全。因为哈希函数的抗原像性只能保证当 x 是在{0, 1}n这样大的空间里面选取的时候，求H(x)的逆是困难的，但是并没有保证当 x 是从别的某个空间或者按照某个分布选择时，求H(x)的难度。而且，抗原像性并没有对求H(x)的的时间进行具体的约束。

为了解决上面所说的安全威胁，可以使用"慢"的哈希函数或者使用多次迭代的哈希函数，从而增加敌手破解的时间。不过为了用户体验，需要将迭代次数设置的适当。

还有一种机制叫做"加盐"，当一个用户进行登录的时候，主机或生成一个长的用户独有的随机数s（就是所谓的“盐”），并且存储(s, hpw=H(s,pw))，而不是像之前那样简单的存储H(pw)。

因为s对敌手是未知的，所以破解这个密钥对于敌手是十分低效率的。

密钥推导

在有的时候，对于通信双方来说，依靠共享的信息(如密码或非均匀分布的生物特征数据)是很方便的。

通信双方可以尝试直接使用他们共享的信息作为密钥，但通常这是不安全的。因为，例如，私钥加密方案都采用统一分布的密钥。此外，共享的数据甚至可能没有用作密钥的正确格式。

最小熵：如果对于每个固定值X Pr_X←x [X = x] ≤ 2^-m，则概率分布X具有m位最小熵。也就是说，即使最可能的结果发生的概率也不超过2^-m。

分布的最小熵用于度量敌手从分布中猜测抽样值的概率。攻击者的最佳策略是猜测最有可能的值，因此，如果分布具有最小熵m，则攻击者的正确猜测概率最多为2^-m。

最小熵的一个扩展叫做计算最小熵，它与最小熵的区别在于该分布只需要在计算上与具有给定最小熵的分布不可区分性。

密钥推导函数提供了一种从任何高(计算)最小熵分布中获得均匀分布字符串的方法：

考虑攻击者对H(X)的不确定性，其中X是从最小熵m的分布中采样的(作为一个技术点，我们要求分布与H无关)。攻击者对H的每个查询都可以看作是对X值的“猜测”;根据分布的最小熵假设，攻击者对H进行q查询，其查询H(X)的概率最大为q·2^-m。如果攻击者没有向H查询X，那么H(X)是一个统一分布的字符串。

承诺方案

承诺方案允许通信方通过发送一个“承诺值” com 来承诺某个消息m。

承诺方案具有看似矛盾的性质：

• 隐藏性：com不能泄露m的信息。
• 绑定性：通信方如果已经对消息m做出了承诺com，那么com就不能是另一条不同的消息m'的承诺。

承诺方案事实上可以看作一个消息的数字信封：将消息密封在信封中并将其交给另一方可以保护隐私(直到打开信封)并具有约束力(因为信封是密封的)。

一个承诺方案的形式化定义如下：

• Gen：一个随机化的算法，用于输出一个公共参数params
• Com：一个以公共参数params和一条消息m∈{0, 1}n作为输入，然后输出一个承诺com。为了随机化，选择一个随机数 r ，计算com := Com(params , m; r)

承诺过程：发送方随机的选择一个随机数r，计算com := Com(params, m; r)，然后将其发送给接收方。

兑现承诺过程：发送方随后可以通过发送(m, r)给接收方来兑现承诺。接收方需要检验Com(params, m; r)是否等于com。

承诺方案的安全模型Hiding_{A, Com}(n)：

1. 运行Gen(1ⁿ)获取公共参数params
2. 敌手A将params作为输入，然后输出一对明文m₀, m₁
3. 随机选择b∈{0, 1}，然后计算com := Com(params, m_b; r)，并将com返回给敌手A
4. 敌手输出一个b’
5. 如果b‘ = b，则这个实验输出1

BindingA, com(n)：

1. 运行Gen(1n)获取公共参数params
2. 敌手A将params作为输入，然后输出(com, m, r, m', r')
3. 如果m ≠ m'并且Com(params, m; r) = com = Com(params, m'; r')，则这个实验输出1

定义：如果存在一个可忽略函数negl能够满足：Pr[HidingA,com(n)=1] ≤ 1/2 + negl(n) 并且Pr[BindingA,com(n)=1] ≤ 1/2 + negl(n)，则称这个承诺方案是安全的。

很容易从一个哈希函数 H 构造一个安全的承诺方案：需要对某条消息进行承诺时，随机的选择一个r∈{0, 1}n，然后输出com := H(m||r)，因为哈希函数是不需要密钥的，所以Gen算法也不需要。

隐藏性：由哈希函数的抗原像性，敌手并不能从com中获取关于m的信息。

绑定性：由于哈希函数的抗碰撞性。