LOJ 162. 快速幂 2

https://loj.ac/p/162

用式子表示一下快速幂的原理：

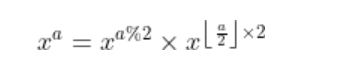
计算这个的复杂度在于后半部分

如果每次折半（即除2）改为每次除3

原理就变为

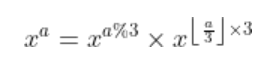
 代码如下

int poww(int a,int b)
{
	int c=1;
	//for(;b;a=1ll*a*a%mod,b>>=1)
	//	if(b&1) c=1ll*c*a%mod;
	while(b)
	{
		if(b%3==1) c=1ll*c*a%mod;
		else if(b%3==2) c=1ll*c*a*a%mod;
		a=1ll*a*a*a;
		b/=3;
	}
	return c;
}

同理，我们可以把原理改为

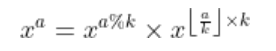
后面仍然需要快速幂，我们可以预处理

取k=sqrt(p)

为了保险取k=sqrt(p)+1

预处理x^i 和 x^i^k,0<=i<=k

对于每次询问就可以O(1)回答

预处理复杂度为sqrt(p)*log(p)

#include<cmath>
#include<cstdio>

const int mod=998244352;

int k=sqrt(mod)+1;

int xp[100001],xp2[100001];

int main() 
{
    int x,n,y;
    scanf("%d%d",&x,&n);
    xp[0]=1;
    xp2[0]=1;
    for(int i=1;i<=k;++i)  xp[i]=1ll*xp[i-1]*x%mod;
    for(int i=1;i<=k;++i)  xp2[i]=1ll*xp2[i-1]*xp[k]%mod;
    for(int i=1;i<=n;++i) 
    {
        scanf("%d",&y);
        printf("%d ",1ll*xp[y%k]*xp2[y/k]%mod);
    }
}