[Ahoi2008]Meet 紧急集合

1787: [Ahoi2008]Meet 紧急集合

Time Limit: 20 Sec  Memory Limit: 162 MB
http://www.lydsy.com/JudgeOnline/problem.php?id=1787

Description

Input

Output

Sample Input

6 4
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
2 4 4
6 6 6

Sample Output

5 2
2 5
4 1
6 0

HINT

Source

Day1

结论1：集合点一定在某两个点的lca上

结论2: 3个点两两算出lca，至少有2个lca相同

结论3：不同的那个lca（或3个都相同的lca）就是集合点，3个点到这个点的总距离最小

证明1：如图所示，假设等待点是 3、5、10

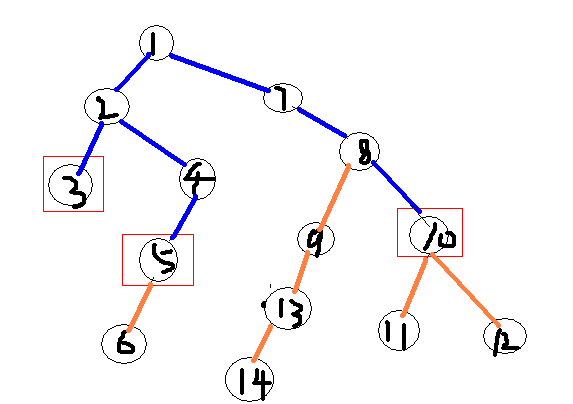
3个点之间的路径用蓝色标注，其余路径用橙色标注

要证明结论1，可以证明以下几点：

① 集合点 选在蓝色路径上的点 一定比 选在橙色路径上的点 更优

    证明：如果集合点选在橙色路径上，即三个点可以不经过集合点到达其他点，那么选橙色路径顶端的蓝色路径上一点会更优

    例如 上图中 8号点要比13号点 更优

② 集合点若选的不是lca，那么集合点越靠近lca，越优。

   我们假设选的点

   证明：设点a，b，c，lca为a和b的lca，设选的点d不是lca，d往lca方向移动一点，设这一点为e

           那么由d向e的过程，会使①2个点的路径长度-1,另外1个点的路径长度+1   或者② 3个点的路径长度各-1

  例子：①在上图中选3、5、10，集合点由4向2转移   ②在上图中好像没有。。。画一个三叉树，集合点由上往下移即可

综上可证结论1

有了结论1，就可以做这个题了，3个lca挨着算一遍即可

结论2关键点：点向上的路径有且只有唯一的一条

结论3关键点：相同的那个lca一定在另一个lca的上面

这样就可以只算那一个lca即可

然后，剩下的难以描述（语文不好），画图意会吧...

代码一：算3个lca && 倍增求lca  && 读入优化    结果：上图第3行

#include<algorithm>
#include<cstdio>
#include<cmath>
#define N 500001
using namespace std;
int n,m,id[N],cnt,fa[N][21],p,deep[N],tmp;
int front[N],next[N*2],to[N*2],tot;
int lca1,lca2,lca3;
int read()
{
    int x=0; char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') { x=x*10+c-'0'; c=getchar();}
    return x;
}
void add(int x,int y)
{
    to[++tot]=y; next[tot]=front[x]; front[x]=tot;
    to[++tot]=x; next[tot]=front[y]; front[y]=tot;
}
void dfs(int x)
{
    id[x]=++cnt;
    for(int i=front[x];i;i=next[i])
     if(to[i]!=fa[x][0]) 
     {
          fa[to[i]][0]=x;
          deep[to[i]]=deep[x]+1;
          dfs(to[i]);
     }
}
int lca(int x,int y)
{
    if(x==y) return x;
    if(id[x]<id[y]) swap(x,y);
    for(int i=p;i>=0;i--)
     if(id[fa[x][i]]>id[y])
      x=fa[x][i];
    return fa[x][0];
}
int dis(int x,int y)
{
    int lc=lca(x,y);
    return deep[x]+deep[y]-2*deep[lc];
}
int main()
{
    n=read(); m=read();
    int x,y,z;
    for(int i=1;i<n;i++)
    {
        x=read(); y=read();
        add(x,y);
    }
    dfs(1);
    p=log(n)/log(2)+1;
    for(int j=1;j<=p;j++)
     for(int i=1;i<=n;i++)
      fa[i][j]=fa[fa[i][j-1]][j-1];
    int ans1,ans2,tmp;
    while(m--)
    {
        x=read(); y=read(); z=read();
        lca1=lca(x,y); lca2=lca(x,z); lca3=lca(y,z);
        ans1=lca1; ans2=dis(x,lca1)+dis(y,lca1)+dis(z,lca1);
        tmp=dis(x,lca2)+dis(y,lca2)+dis(z,lca2);
        if(tmp<ans2) 
        {
            ans2=tmp;
            ans1=lca2;
        }
        tmp=dis(x,lca3)+dis(y,lca3)+dis(z,lca3);
        if(tmp<ans2)
        {
            ans2=tmp;
            ans1=lca3;
        }
        printf("%d %d
",ans1,ans2);
    }
}

代码二：算1个lca && 倍增求lca   && 读入优化   结果： 上图第2行

#include<algorithm>
#include<cstdio>
#include<cmath>
#define N 500001
using namespace std;
int n,m,id[N],cnt,fa[N][21],p,deep[N],tmp,ans2;
int front[N],next[N*2],to[N*2],tot;
int lca1,lca2,lca3;
int read()
{
    int x=0; char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') { x=x*10+c-'0'; c=getchar();}
    return x;
}
void add(int x,int y)
{
    to[++tot]=y; next[tot]=front[x]; front[x]=tot;
    to[++tot]=x; next[tot]=front[y]; front[y]=tot;
}
void dfs(int x)
{
    id[x]=++cnt;
    for(int i=front[x];i;i=next[i])
     if(to[i]!=fa[x][0]) 
     {
          fa[to[i]][0]=x;
          deep[to[i]]=deep[x]+1;
          dfs(to[i]);
     }
}
int lca(int x,int y)
{
    if(x==y) return x;
    if(id[x]<id[y]) swap(x,y);
    for(int i=p;i>=0;i--)
     if(id[fa[x][i]]>id[y])
      x=fa[x][i];
    return fa[x][0];
}
int dis(int x,int y)
{
    int lc=lca(x,y);
    return deep[x]+deep[y]-2*deep[lc];
}
int main()
{
    n=read(); m=read();
    int x,y,z;
    for(int i=1;i<n;i++)
    {
        x=read(); y=read();
        add(x,y);
    }
    dfs(1);
    p=log(n)/log(2)+1;
    for(int j=1;j<=p;j++)
     for(int i=1;i<=n;i++)
      fa[i][j]=fa[fa[i][j-1]][j-1];
    while(m--)
    {
        x=read(); y=read(); z=read();
        lca1=lca(x,y); lca2=lca(x,z); lca3=lca(y,z);
        if(lca1==lca2) tmp=lca3;
        else if(lca1==lca3) tmp=lca2;
        else tmp=lca1;
        ans2=dis(x,tmp)+dis(y,tmp)+dis(z,tmp);
        printf("%d %d
",tmp,ans2);
    }
}

代码三：算1个lca && 树链剖分求lca && 读入优化  结果：上图第1行

#include<algorithm>
#include<cstdio>
#include<cmath>
#define N 500001
using namespace std;
int n,m,tmp,ans;
int front[N],next[N*2],to[N*2],tot;
int lca1,lca2,lca3;
int son[N],deep[N],bl[N],fa[N];
int read()
{
    int x=0; char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') { x=x*10+c-'0'; c=getchar();}
    return x;
}
void add(int x,int y)
{
    to[++tot]=y; next[tot]=front[x]; front[x]=tot;
    to[++tot]=x; next[tot]=front[y]; front[y]=tot;
}
void dfs1(int x)
{
    son[x]++;
    for(int i=front[x];i;i=next[i])
     if(to[i]!=fa[x]) 
     {
          fa[to[i]]=x;
          deep[to[i]]=deep[x]+1;
          dfs1(to[i]);
          son[x]+=son[to[i]];
     }
}
void dfs2(int x,int top)
{
    bl[x]=top;
    int y=0;
    for(int i=front[x];i;i=next[i])
     if(to[i]!=fa[x]&&son[to[i]]>son[y]) y=to[i];
    if(!y) return;
    dfs2(y,top);
    for(int i=front[x];i;i=next[i])
     if(to[i]!=fa[x]&&to[i]!=y) dfs2(to[i],to[i]); 
}
int lca(int x,int y)
{
    while(bl[x]!=bl[y])
    {
        if(deep[bl[x]]<deep[bl[y]]) swap(x,y);
        x=fa[bl[x]];
    }
    return deep[x]<deep[y] ? x:y;
}
int dis(int x,int y)
{
    int lc=lca(x,y);
    return deep[x]+deep[y]-2*deep[lc];
}
int main()
{
    n=read(); m=read();
    int x,y,z;
    for(int i=1;i<n;i++)
    {
        x=read(); y=read();
        add(x,y);
    }
    dfs1(1);
    dfs2(1,1);
    while(m--)
    {
        x=read(); y=read(); z=read();
        lca1=lca(x,y); lca2=lca(x,z); lca3=lca(y,z);
        if(lca1==lca2) tmp=lca3;
        else if(lca1==lca3) tmp=lca2;
        else tmp=lca1;
        ans=dis(x,tmp)+dis(y,tmp)+dis(z,tmp);
        printf("%d %d
",tmp,ans);
    }
}

上图第4行为 算3个lca && 倍增求lca